四谷大塚 予習シリーズ 算数 徹底解説 5年上第11回 場合の数-ならべ方-クイックラーニング

予習シリーズ5年前期で「場合の数」を学びます。「場合の数」のうち、11回では「ならべ方」を、12回では「組み合わせ方」を扱います。

「場合の数」と言えば、中学生のときに「確率」ってやったわ。

よく覚えていますね。ただ「場合の数」と「確率」はちょっと違います。
「場合の数」は、例えば、「4人の生徒(A, B, C, Dとします)から3人を選んでチームを作る場合、何通りのチームが作れるか」というように、「どれだけの異なる選び方が存在するか」を数えます。
対して「確率」は、例えば、「4人の生徒(A, B, C, Dとします)がいるとして、彼らがランダムに名前を書いた帽子から自分の名前を引くというゲームをするとき、全員が自分の名前を引く確率はどれくらいか」というように、「特定の事象が起こる確率」を計算します。

分かったわ。中学受験では「どれだけの異なる選び方が存在するか」を数えればいいのね。

はい、そうです。では、さっそく問題を見ていきましょう!



予習シリーズ算数 場合の数(ならべ方) 例題1

例題1のポイントは「大小2つのさいころを同時にふる」です。このように問われたら、反射的に下のような図を書きましょう。

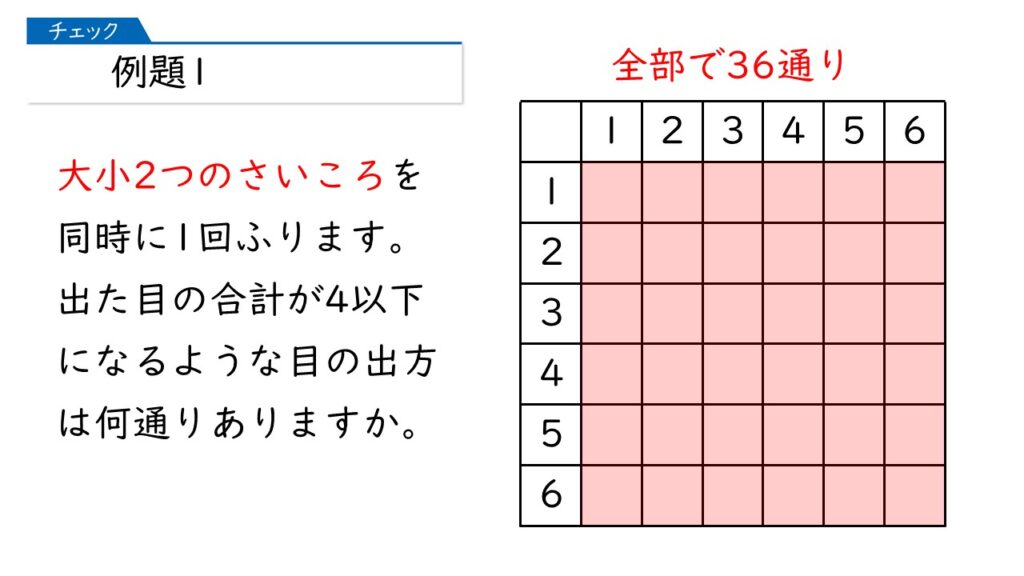
大きいさいことと小さいさいころの目の組み合わせが全部で36通りあるってことね。

そうです! この図を書いてから、条件を確認しましょう。

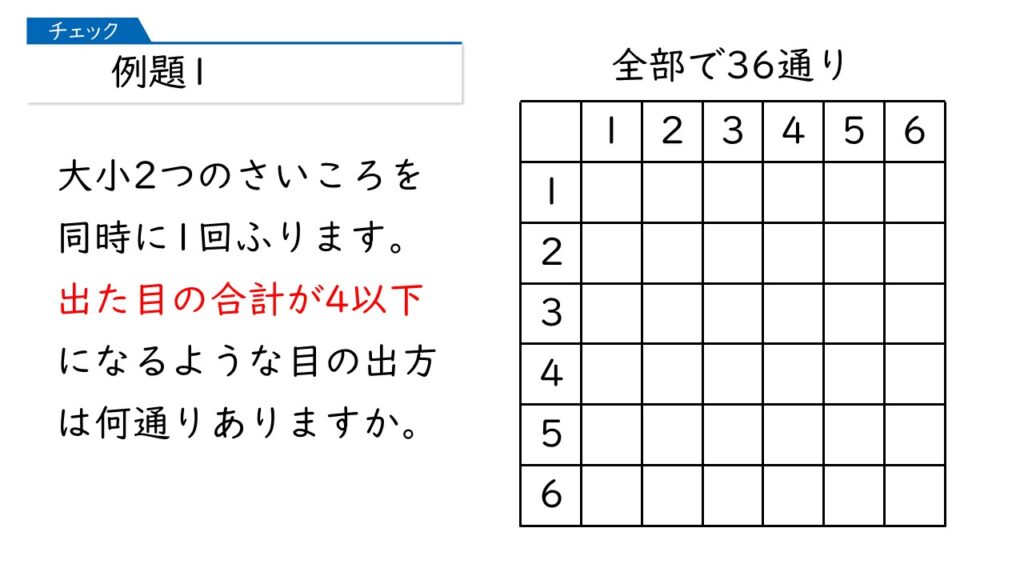
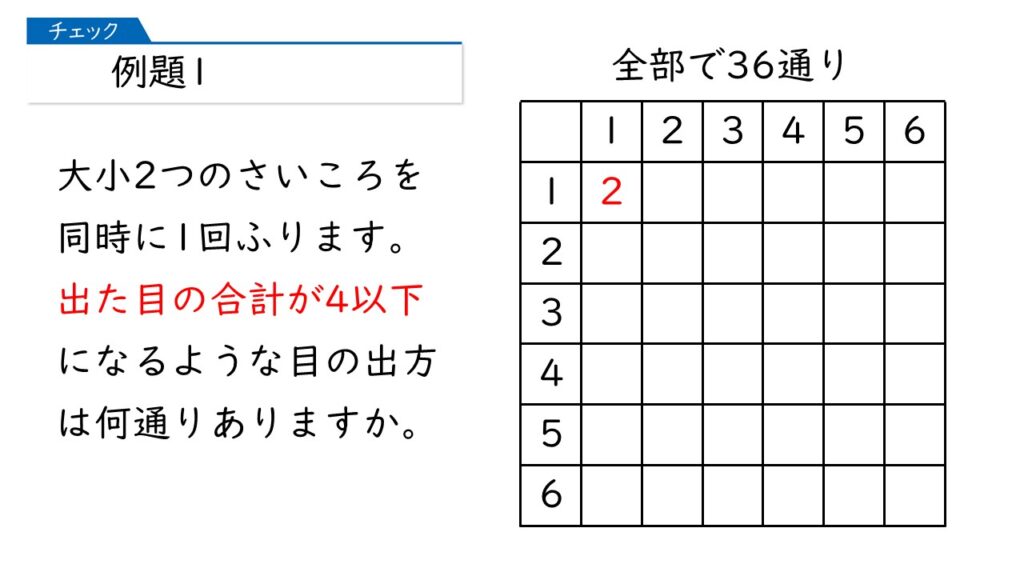
「出た目の合計が4以下」とあるから、( 1,1 )( 1, 2 )( 2, 1 )… というふうに順々に調べていけばいいのね。

そうです!では、調べていきましょう。


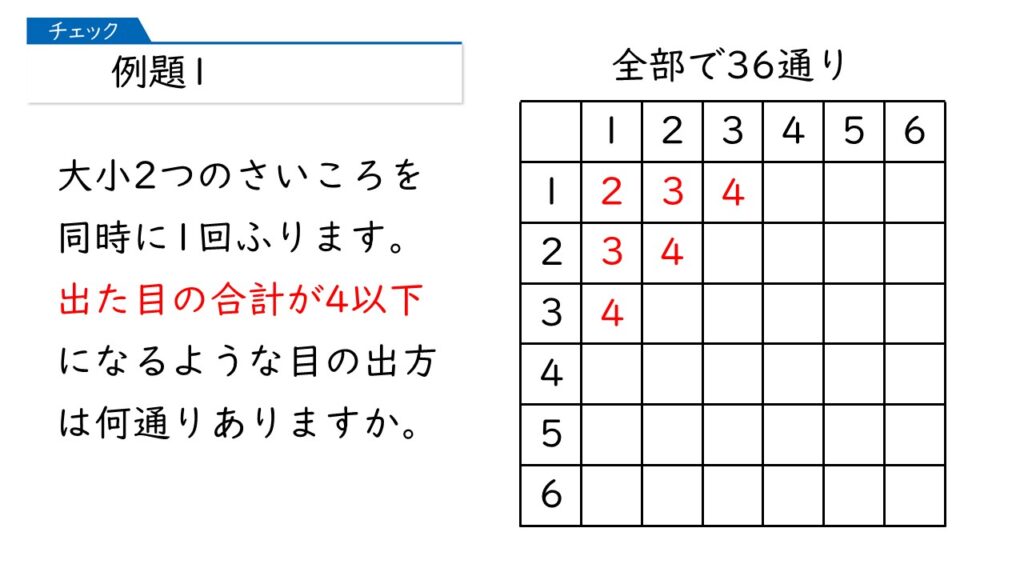
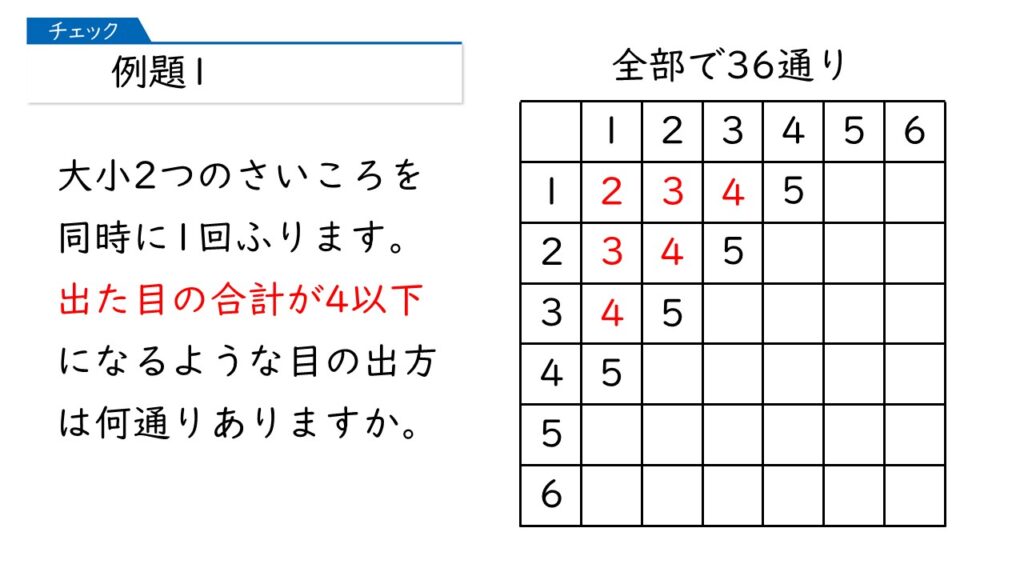
出た目の合計が4以下とありますから、ここで打ち止めですね。答えは何通りになりますか?

かんたんだわ! 6通り!

その通りです! 図を書くといろいろと応用がききますよ。

予習シリーズ算数 場合の数(ならべ方) 例題2
例題2に進みましょう。

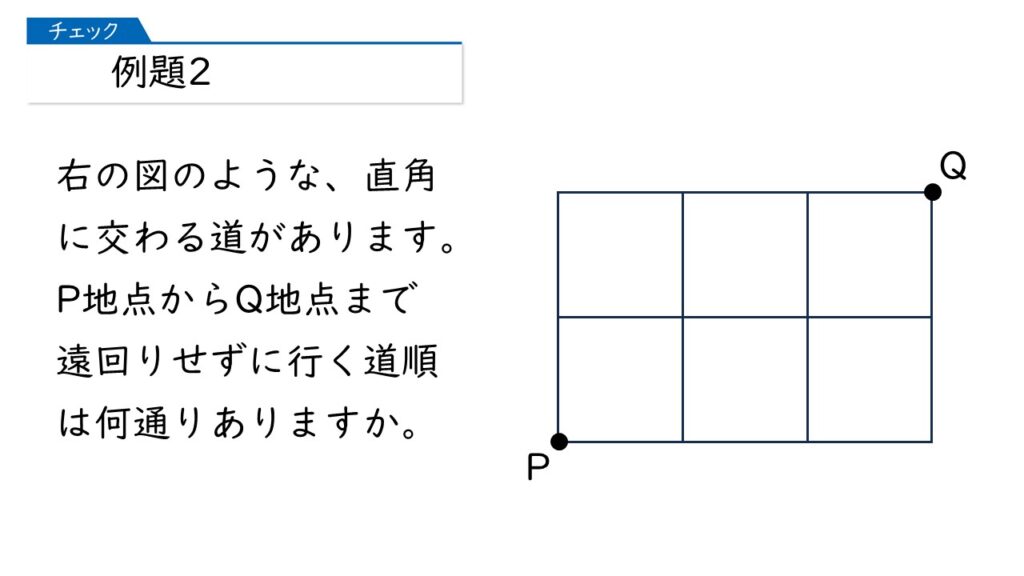
目が回りそうだわ…

大丈夫ですよ! 問題に「遠回りせずに」って書いて書いてありますから、進み方は「上」または「右」だけです。
テクニックを覚えようとする人もいますが、あまり感心しません。この問題は、途中の道が通れないというパターンもありますから、途中経過をしっかり理解しましょう。
まず、下の図で、P地点からA地点に行く道順は何通りありますか?


これはかんたんだわ。右回りと左回りで2通りね。

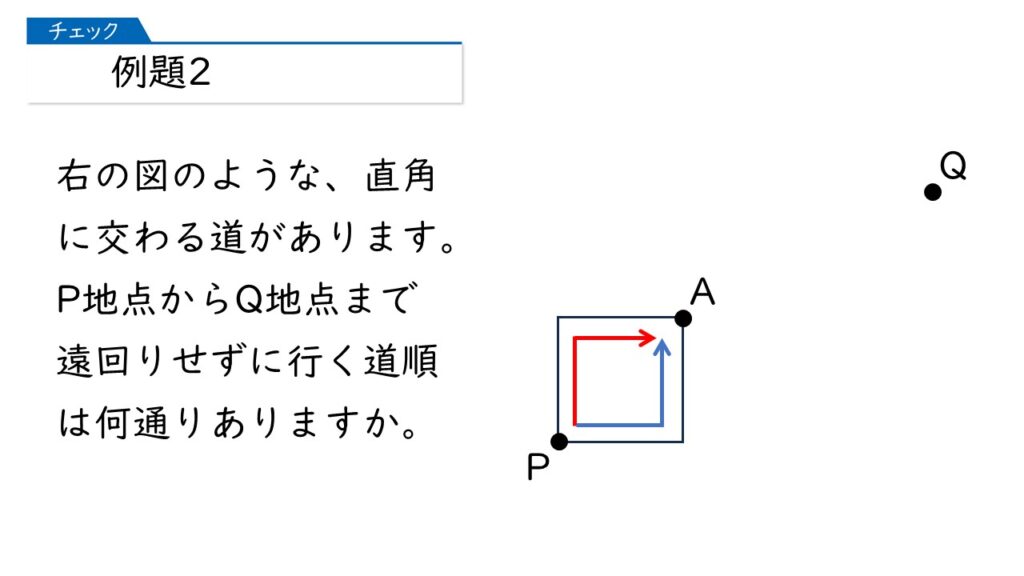
はい、そのとおりです。下の図のように「1+1=2(通り)」と求められることを確認してください。

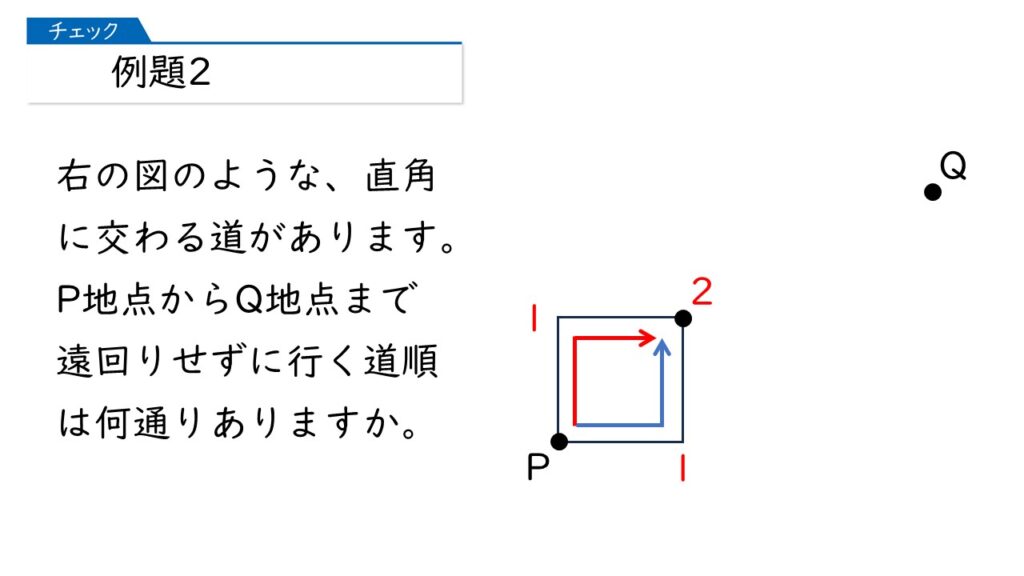
次に、下の図で、P地点からB地点に行く道順は何通りありますか?


下の図の黄、赤、青の線だから、3通りね!

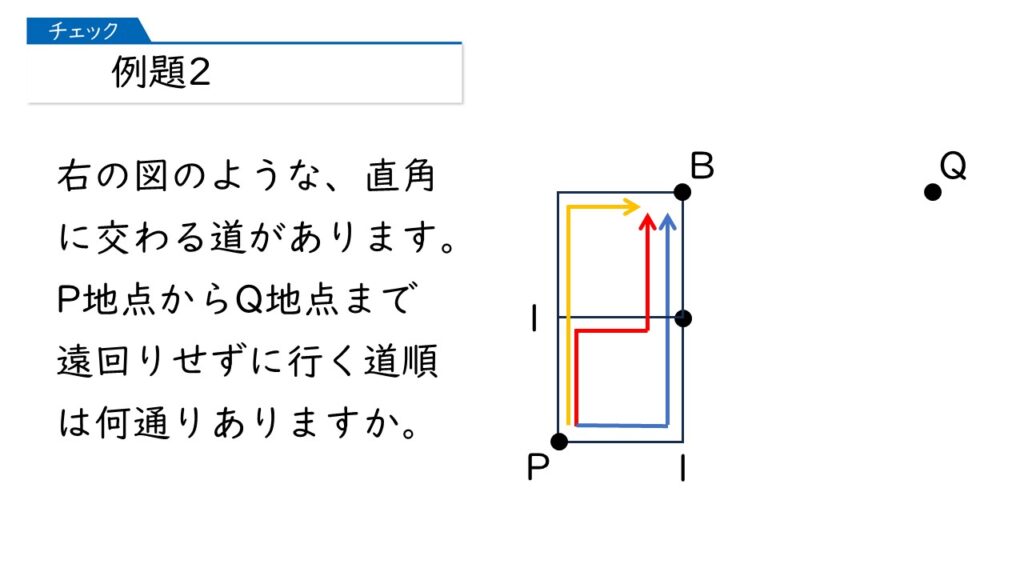
おおっ、その通りです! 下の図のように「1+2=3(通り)」と求められることを確認してください。

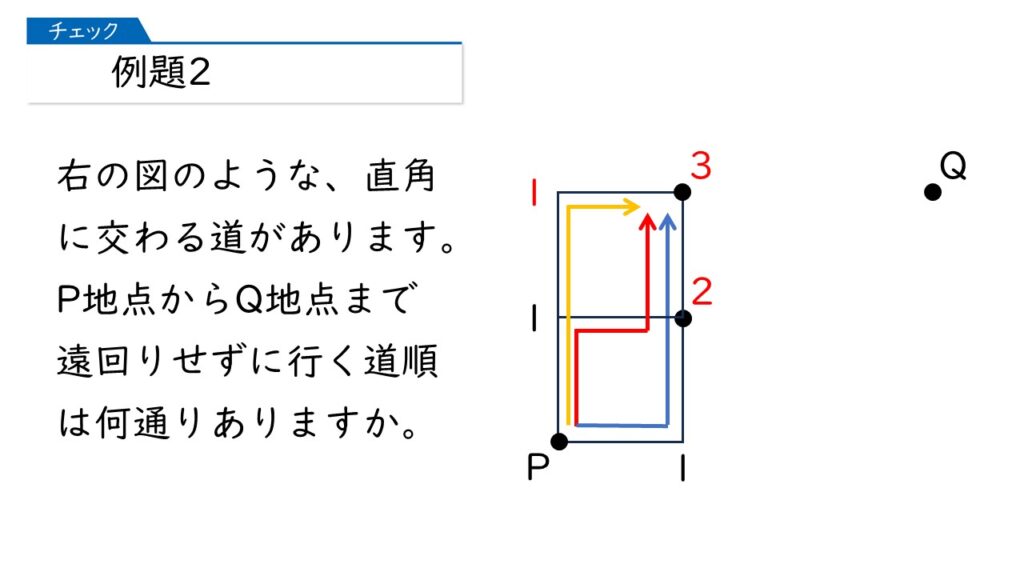
次に、下の図で、P地点からC地点に行く道順は何通りありますか?


B地点と同じように考えられるから、3通り!

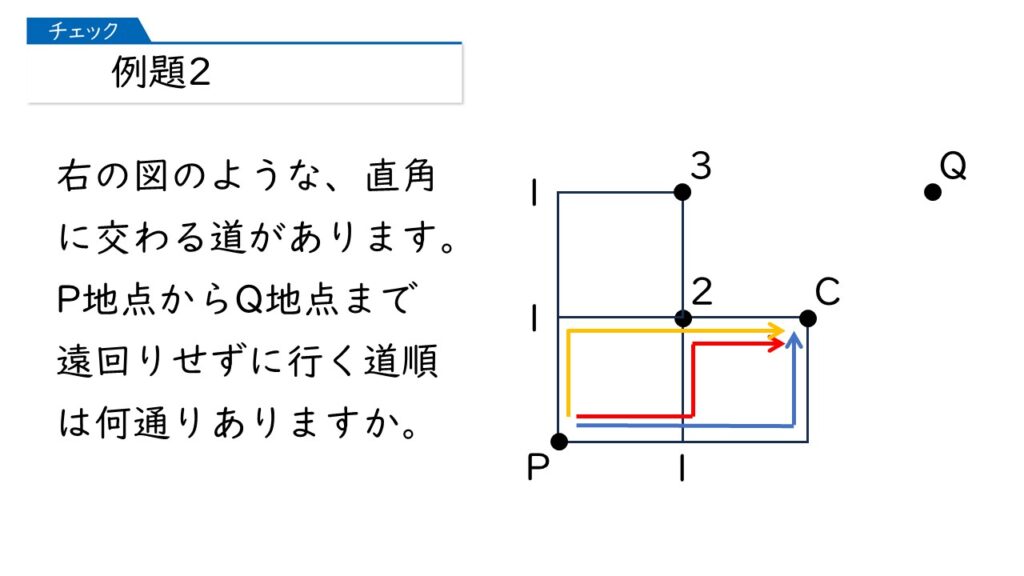
よく見抜きましたね! ここでも、下の図のように「1+2=3(通り)」と求められることを確認してください。


次に、下の図で、P地点からD地点に行く道順は何通りありますか?

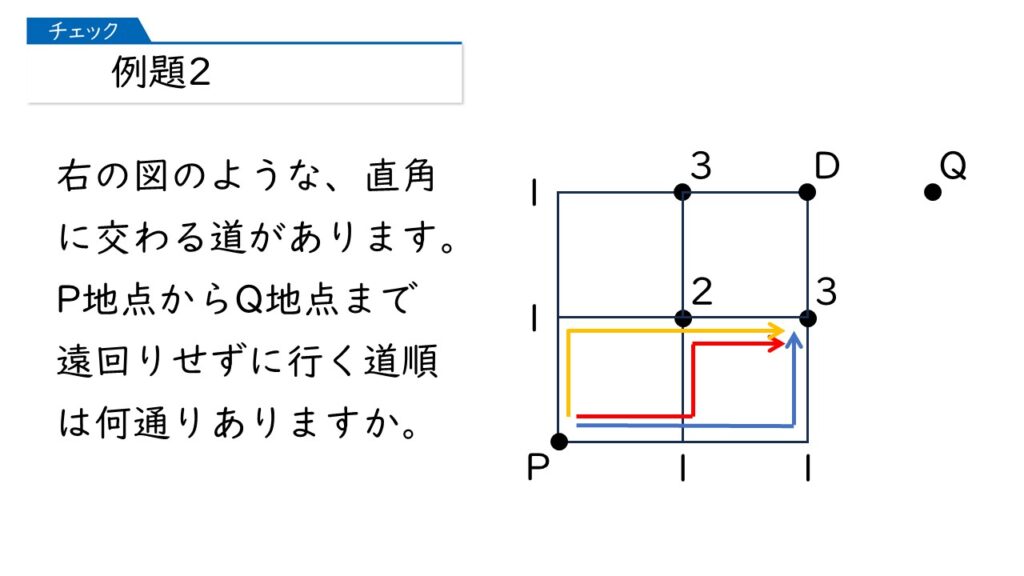
下の図のように、C地点から上に上がればいいから、ここでも3通りかしら?


惜しいです! 下の図のように、B地点からの道順もありますよ。


そうだったわ。そうすると、P地点からD地点に行く道順は6通りなのね。

その通りです! 下の図のように、下の図のように「3+3=6(通り)」と求められることを確認してください。


次に、下の図で、P地点からE地点に行く道順は何通りありますか?


下の図のように、右下を通る方法もあるわ。


そうですね。その通り方を加えて、4通りです。下の図のように「3+1=4(通り)」と求められることを確認してください。


さあ、ここで最後です。P地点からQ地点に行く道順は何通りありますか?

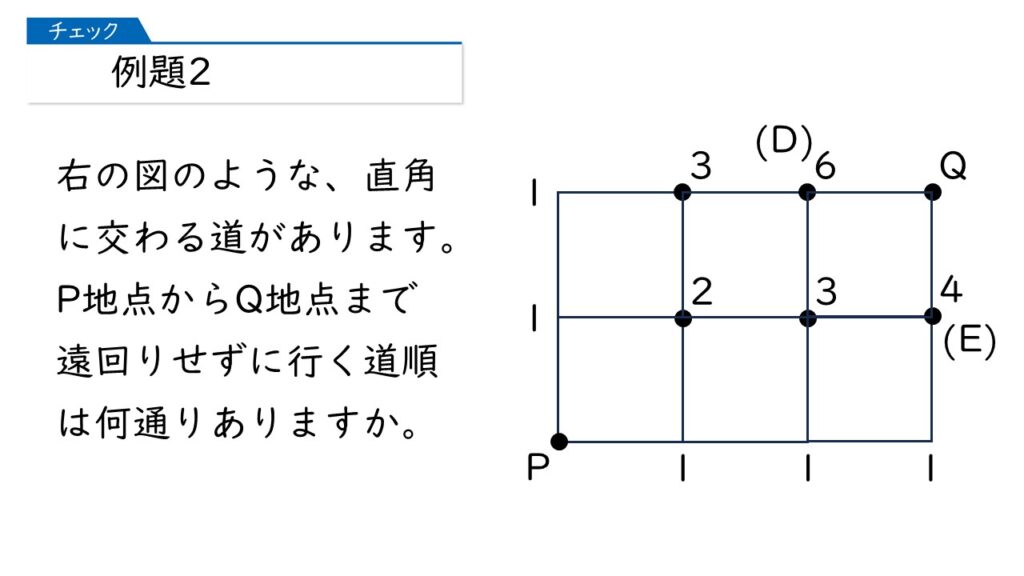
分かったわ! 6+4=10通りね!

正解です! おめでとうございます!
大事なことは、道順を具体的にイメージしながら解くことです。そうしないと、基本問題や練習問題を解くときに困ってしまいますから。

予習シリーズ算数 場合の数(ならべ方) 例題3
例題3(1)の解き方
次は、例題3(1)ですね。

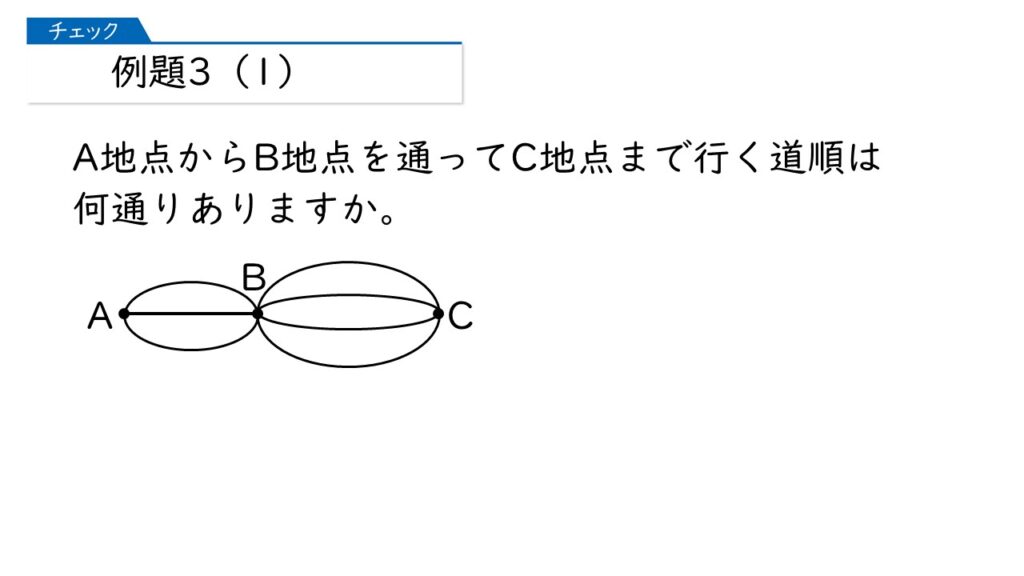
具体的に考えていきましょう! 下の図で、A地点~B地点を赤い道を通ってC地点に行く方法は何通りありますか?

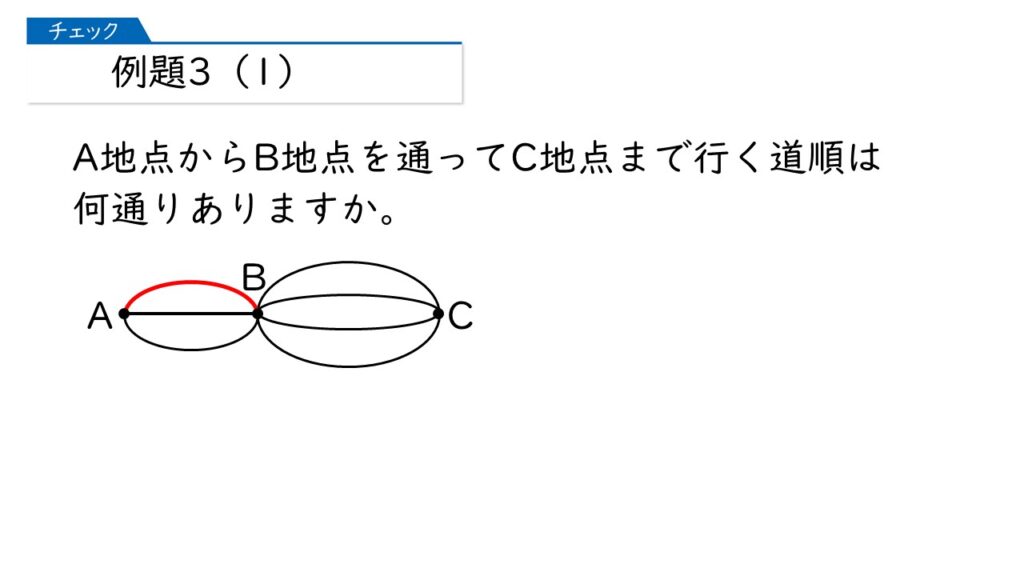
B地点からC地点に行く道は4本あるから、4通りね。

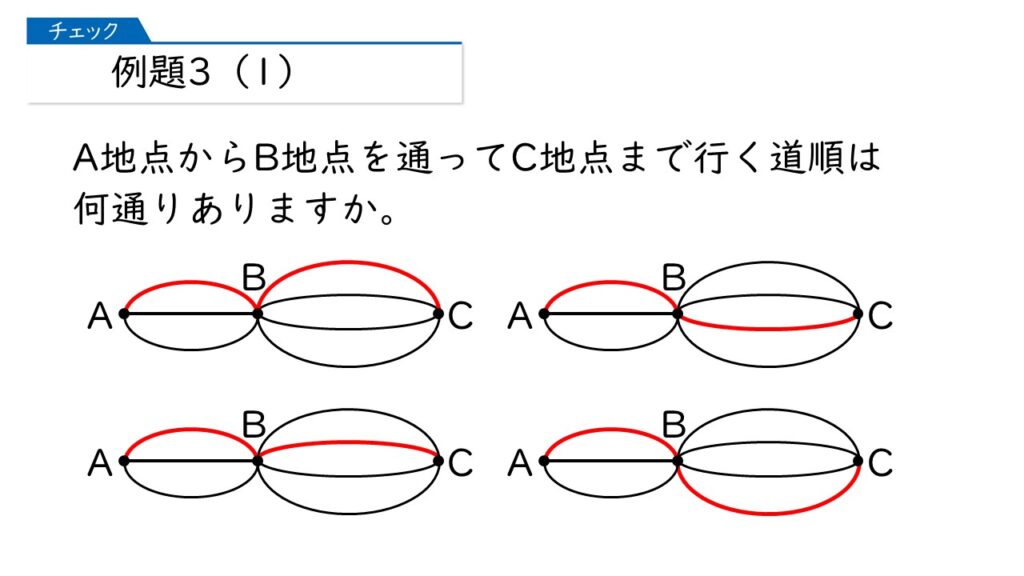
そうですね! では、A地点~B地点を黄色い道を通ってC地点に行く方法は何通りありますか?

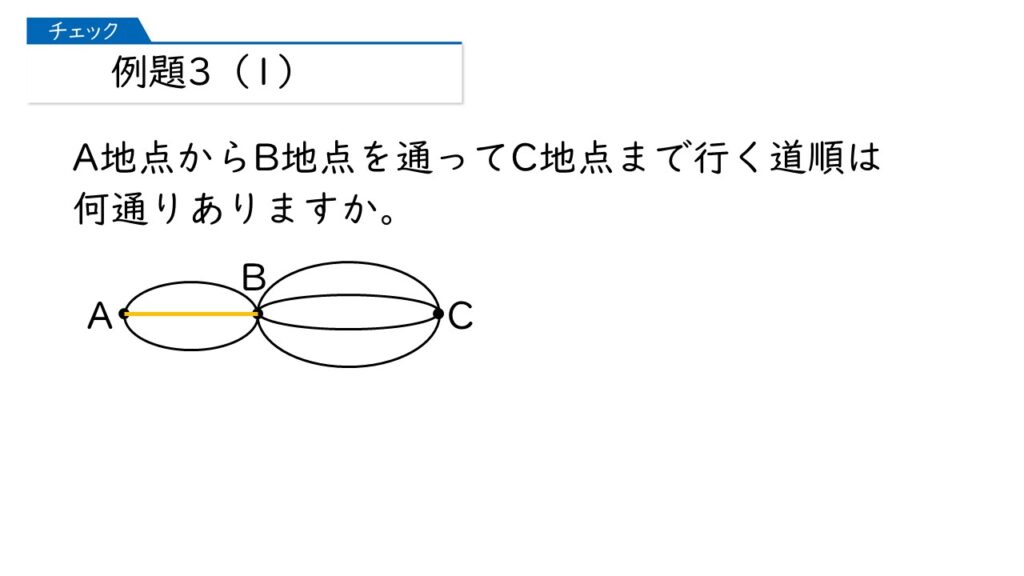
この場合も、B地点からC地点に行く道は4本あるから、4通りね。

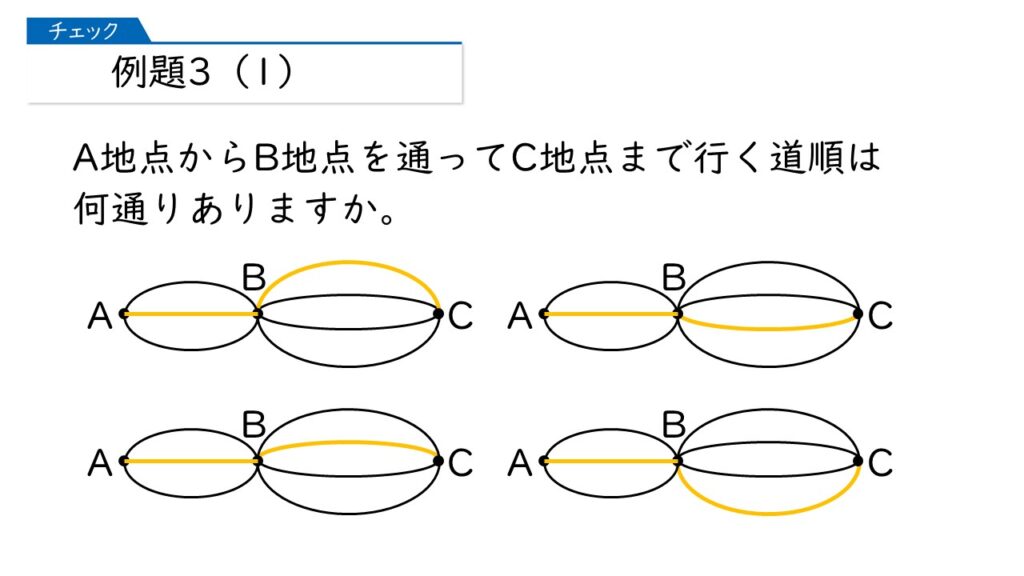
そうですね! そうすると、もう答えはでますか?

A地点~B地点を緑色の道を通ってC地点に行く方法も4通りだから、全部で、3×4=12通りね!


正解です! A地点~B地点の道順は3通りで、B地点~C地点の道順は4通りなので、3×4=12(通り) と求めることができますね。

例題3(2)の解き方
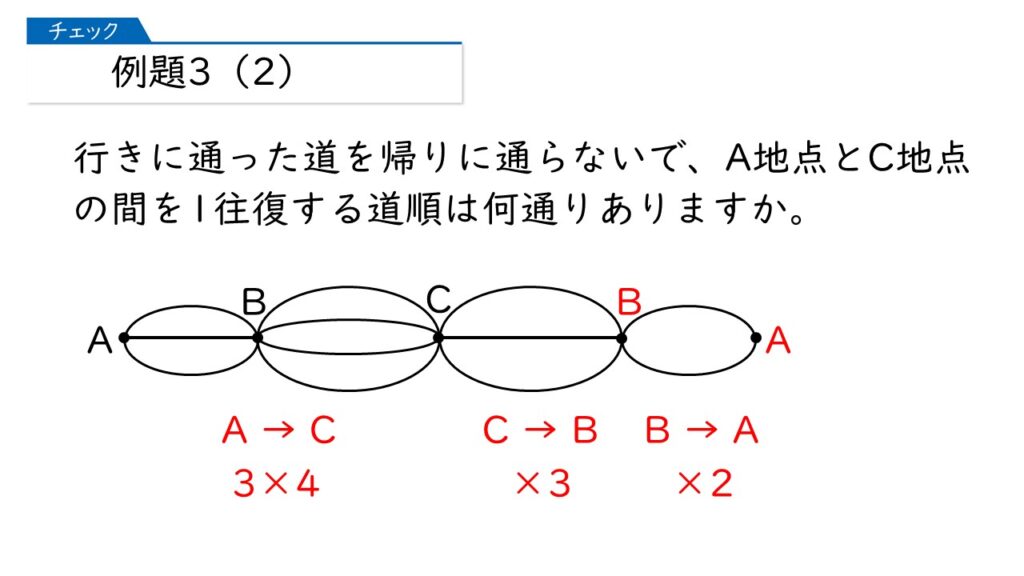
では、例題3(2)はどうでしょうか。例題3(2)は「行きに通った道を帰りに通らないでもどってくる」という設定です。
まず、(1)でやったように、A地点からC地点に行く道順は、3×4=12通りですね。

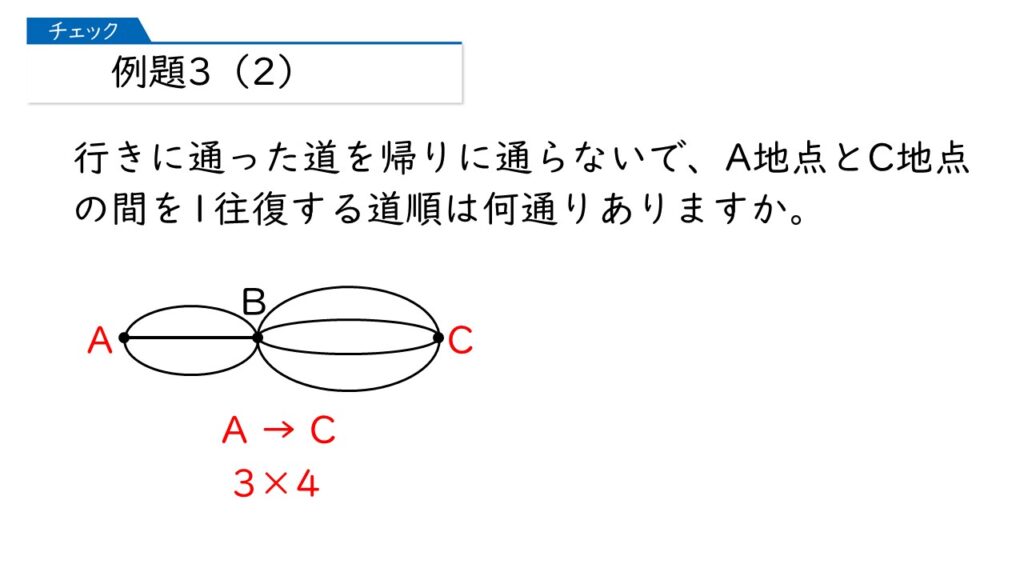
では、ここから引き返します。C地点からB地点にもどる道順は何通りありますか?

行きに通った道は通れないから、4-1=3通りね!

その通りです! 下の図のように考えればいいですよ。

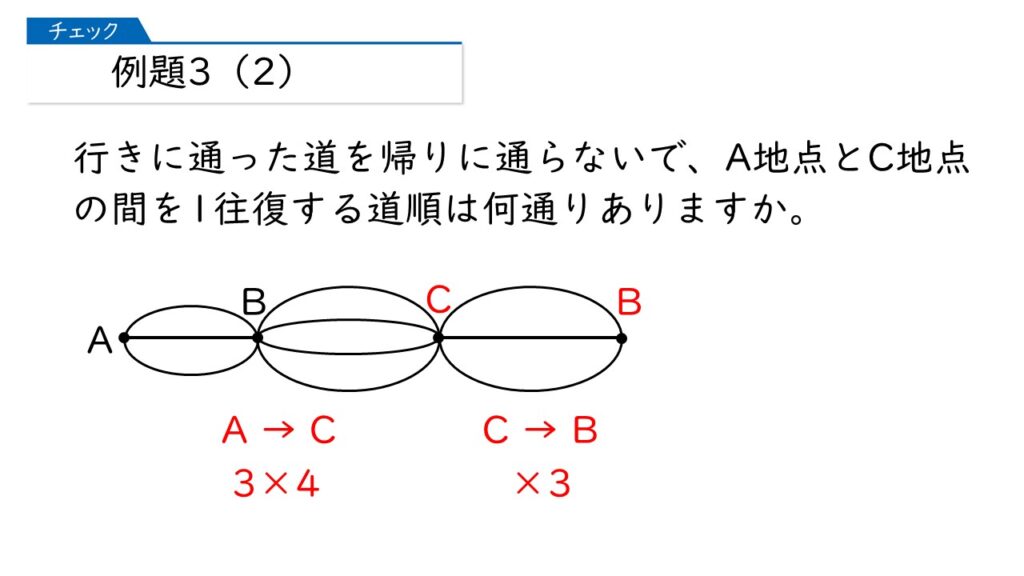
そうすると、答えが出ませんか?

分かったわ! 3×4×3×2=72通りね。

正解です、おめでとうございます!

予習シリーズ算数 場合の数(ならべ方) 例題4
例題4(1)の解き方
さあ、ここから入試本番を意識した重要問題です。


ここからは「樹形図」を書いていきましょう。父、母、兄、妹を、それぞれA~Dとしますね。

「樹形図」って何でしたっけ?

下の図のように、木の枝のように伸ばしていく図ですよ。


思い出したわ! 一番左がAのとき、その右どなりの人がBまたはCまたはDということね。

そうです。では、この樹形図を完成させていきましょう!




一番左の人がAのとき、4人のならび方は6通りですね。答えは全部で何通りですか?

一番左の人がB、C、Dのときも、それぞれ6通りずつあるのね。だから、4×3×2×1=24通りね。


正解です!

例題4(2)の解き方
では、例題4(2)はどうでしょう?


これも樹形図で行けるわ!



なるほど! 一番左が父のときのならび方は、2×1×1=2通りになるのですね。

そうよ。一番左は母の場合もあるから、全部で2×2×1×1=4通りになるわ。


ずいぶん早く解けましたね! 樹形図を書いて上手に整理したおかげだと思います。

予習シリーズ算数 場合の数(ならべ方) 例題5
例題5(1)の解き方
例題5は整数の問題ですね。まず、例だ5(1)を見てみましょう。


これも樹形図を書けばかんたんね。

そうですね。では、樹形図を完成させましょう!
注意が必要なのは、0は百の位の数字としてカウントしてはいけないということです。百の数字を0にしちゃうと、その数は3けたではなくて2けたになってしまいますから。




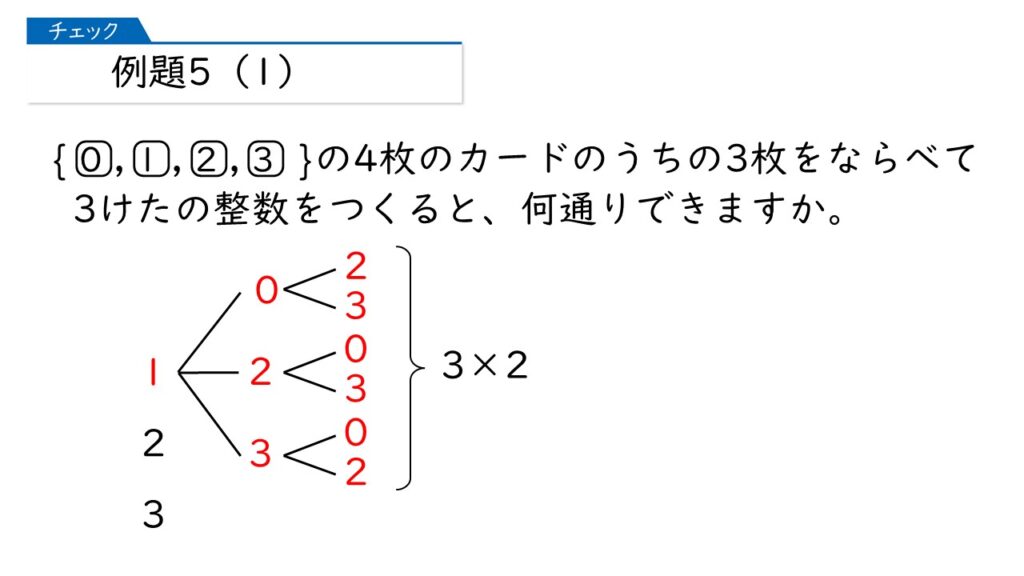
百の位の数字が1のとき、3けたの数字は3×2=6通りできる、ってことですね。

はい。百の位の数字は、1のほか2または3も考えられるから、答えは3×3×2=18通りね。

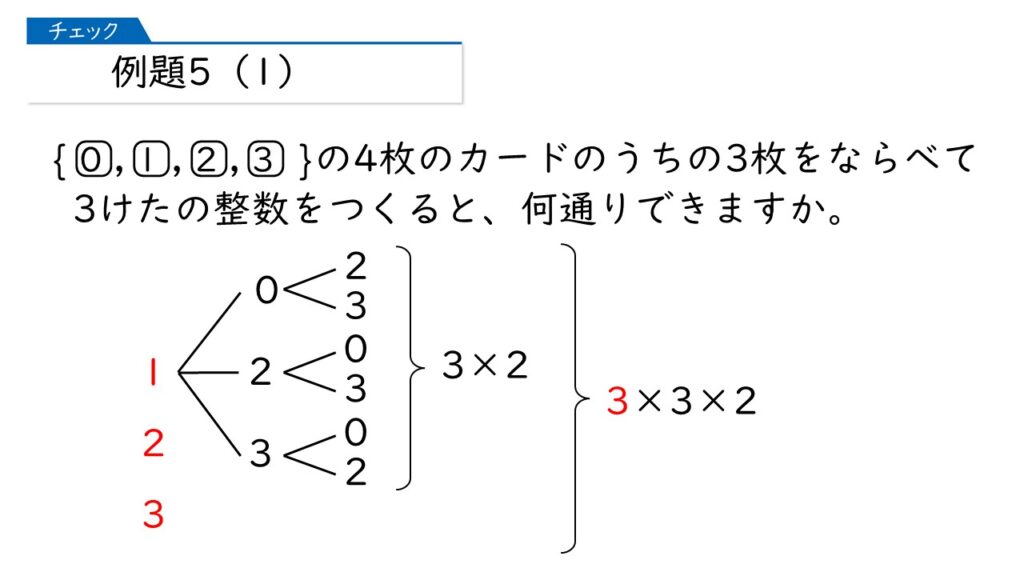
正解です!

例題5(2)の解き方
次に、例題5(2)です。これは少々手ごわいですよ。ポイントは「偶数」になるようにならべなければなりません。


じゃあ、樹形図は書けないってこと?

いえいえ、この問題も樹形図で解決します。
ところで「偶数」というのはどのような数でしたか?

偶数って、1の位が0、2、4、6、8 になる数でしょ。

そうですね。だから、1の位から樹形図を書いていけばいいんです。

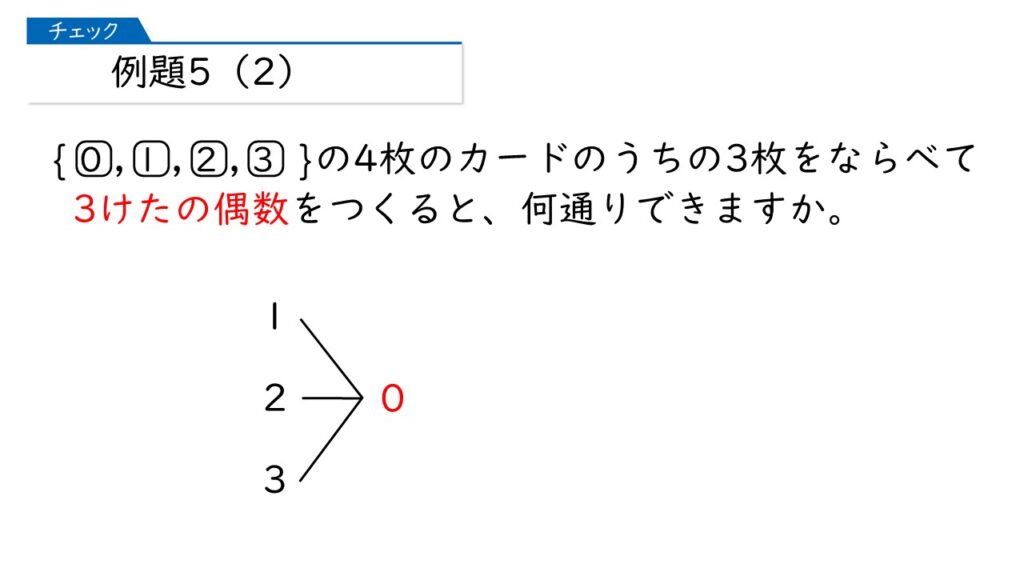
なるほど。1の位が0または2になればいいのね。まずは、1に位が0になる場合を書いてみるわ。

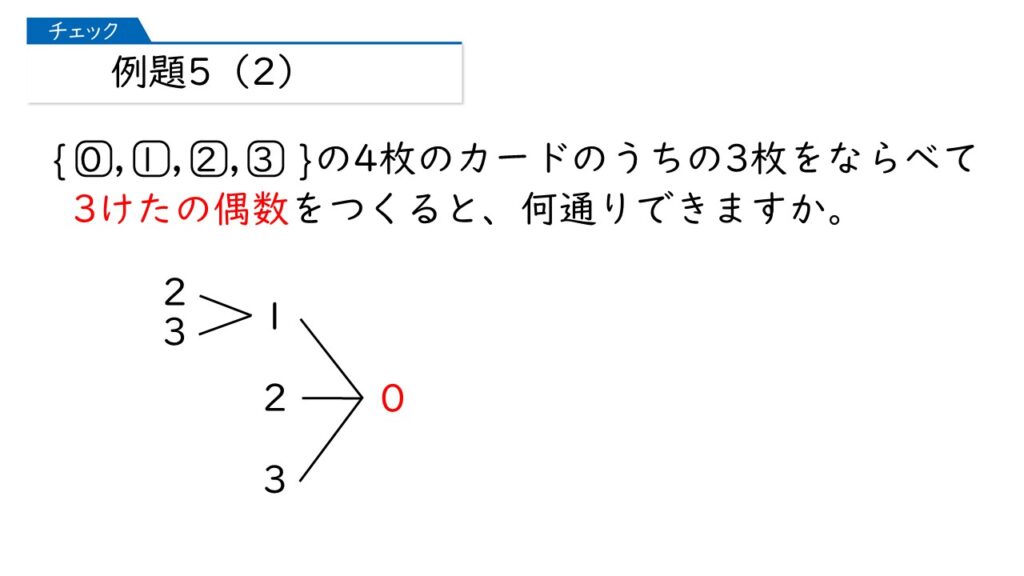
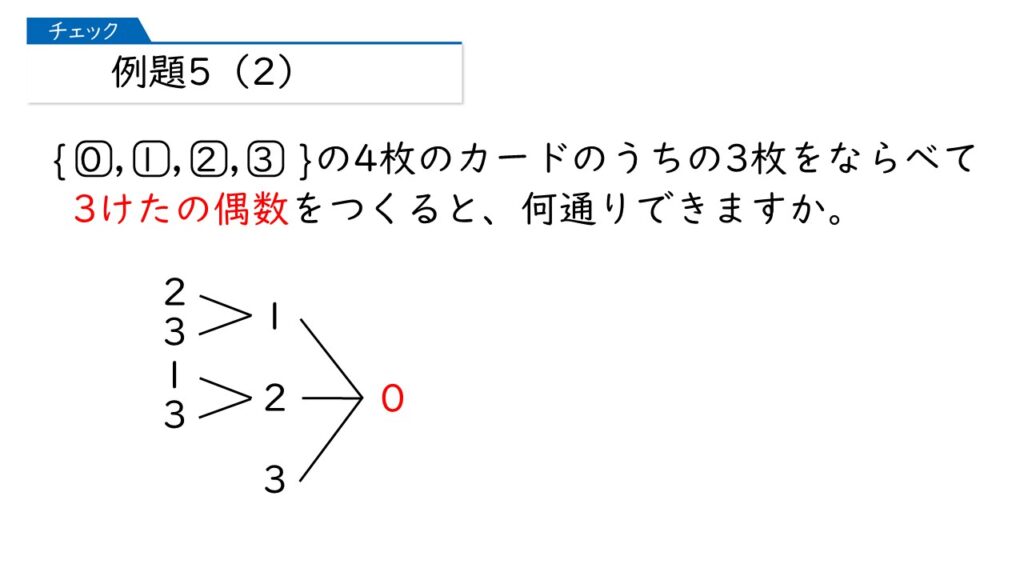
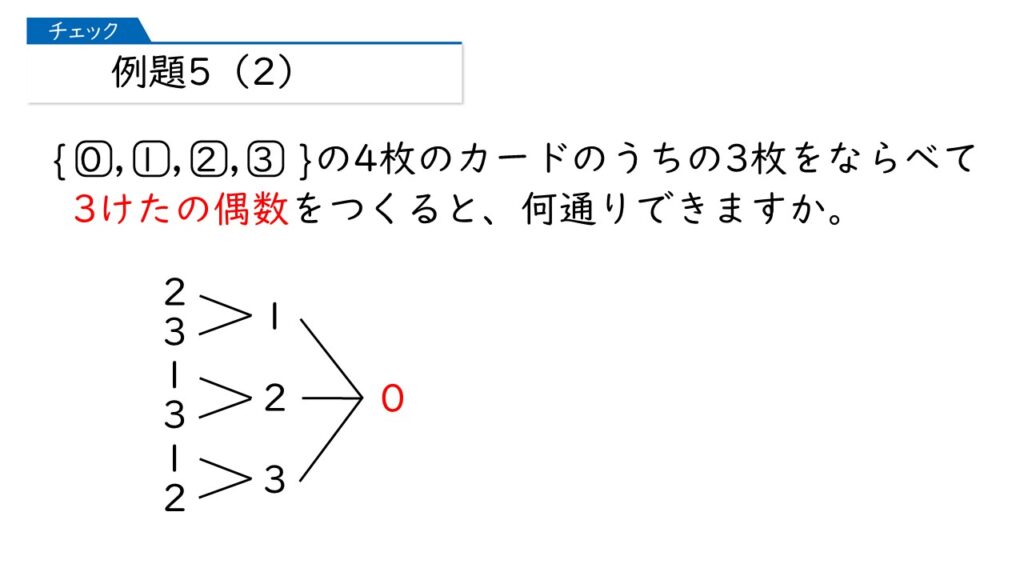
な~んだ、かんたんじゃない? 1の位が0のとき6通りある、だから1の位が2のときも6通り、答えは6×2=12通りでしょ。

いやいや、そうでもないんですよ。1の位が2の場合を書いてみますね。


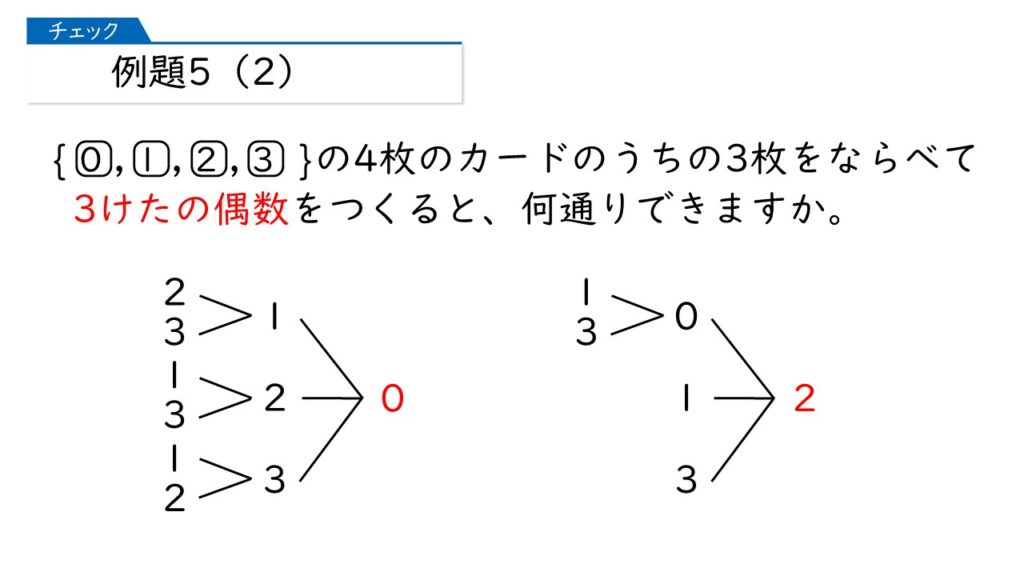

あっ、百の位が0になっちゃうと、2けたになってしまうのね!

そうなんですよ。選択肢に0がある場合は注意を必要なんです。樹形図の続きは次のようになりますね。答えは何通りですか?

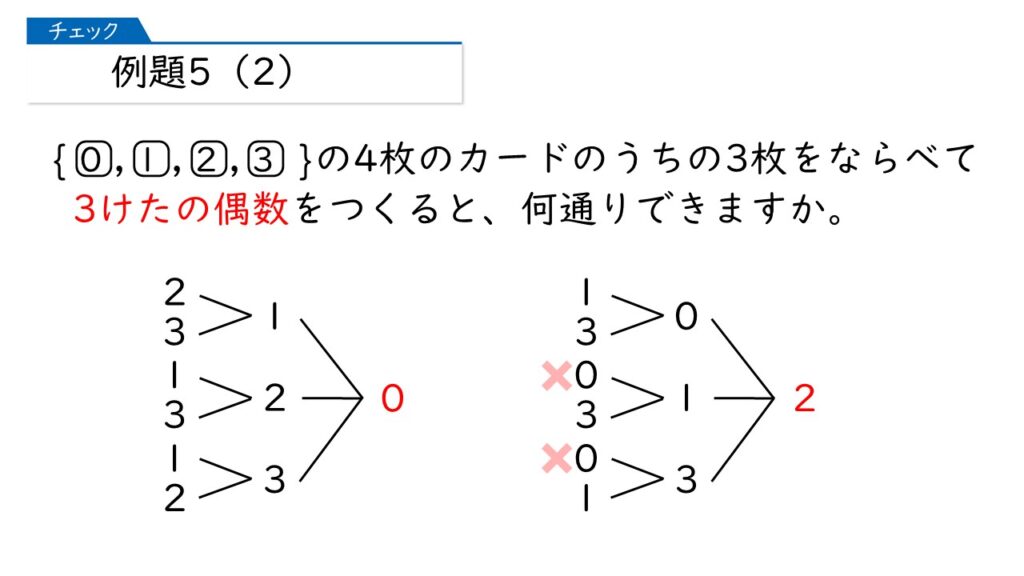
百の位が0になる場合を除いて、10通りが答えだわ。

その通りです。よくできました!

予習シリーズ算数 場合の数(ならべ方) 例題6
例題6(1)の解き方
例題6はぬり分けの問題です。まずは(1)の問題をみてみましょう。


これも樹形図でいけそうね。

はい、その通りです。じゃあ、樹形図を書いていきますね。


一番左のアのところが赤色の場合は、全部で3×2×1=6通りになるのね。なら、答えは、4×3×2×1=24通りね。

その通りです! スラスラ解けましたね。

例題6(2)の解き方
じゃあ、例題6(2)はどうでしょう? (1)とちがって、3色しか使えませんよ。


むむむ…

そんなに怖い顔しなくても…。コツが分かればかんたんですよ! 下の図のように、はなれた2か所が同じ色になればいいんです。


なるほどね~

はなれたところが同じ色になればいいんですけど、ほかにありませんか?

あるわ! アとエが同じ色になればいいのね。


そうです、まだありませんか?

まだあったわ! イとエが同じ色になればいいのね。

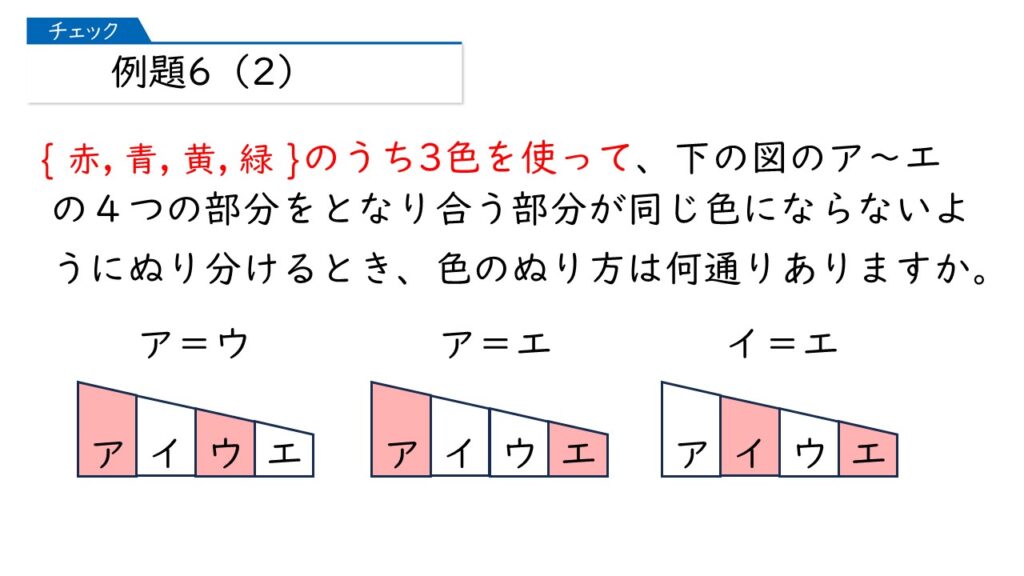
よく見つけましたね。これで、あとは樹形図を書いてオシマイです。赤=A、青=B、黄=C、緑=Dとして書きましょう。

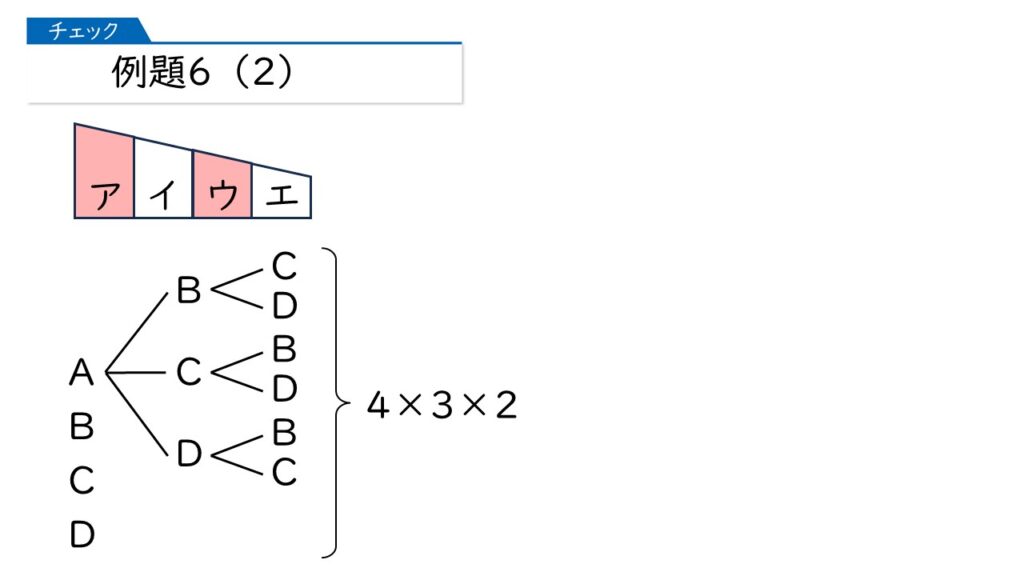
アとウが同じ色になるときは、4×3×2=24通りね。そうすると、ア=エ、イ=エの場合もそれぞれ24通りだから、答えは、3×4×3×2=72通りになるわ。

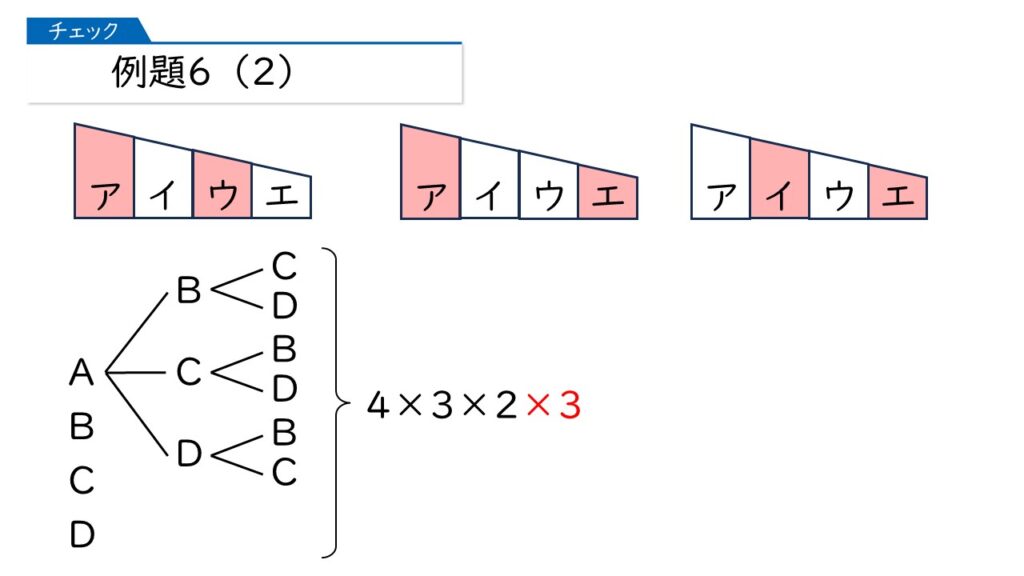
大正解です! おめでとうございます。

場合の数の問題は何となく難しいと思っていたけど、きちんと調べていけば何てことなかったわ。

そう思っていただけるとうれしいです! 次回は、場合の数のうち「組み合わせ方」をやりますね。
ここまでで質問がある方は、下のフォームからお願いします。








第8回.jpg)