四谷大塚 予習シリーズ 算数 徹底解説 5年上第4回 いろいろな差集め算-クイックラーニング

今回は、予習シリーズ算数5年の第4回、いろいろな差集め算を解説しますよ。

「差集め算」って4年のときにやったわ。カンタンそうね!

いやいや、カンタンでもないんですよ、今回は。
でも、予習シリーズにのっている解法のほかに、マルイチ算での解き方も解説しますので、じっくり取り組んでいきましょう!



予習シリーズ算数 いろいろな差集め算 例題1
例題1の解き方
まず、【例題1】から見ていきましょう。これは4年でやったことの復習です。


まず、全体の差「180円」に注目ね!

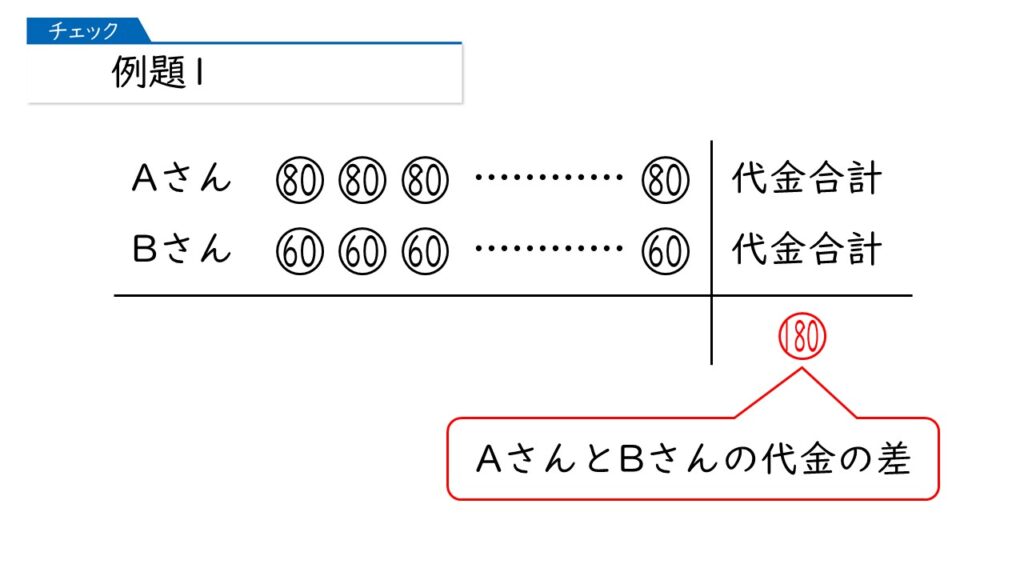
そうですね。次に、一人当たりの差「20円」に注目です。


そうすると、「20×買った個数=180」で、買った個数が分かりますね。


買った個数は、180÷20=9個だから、Aさんが支払ったのは、80円×9個=720円ね。

その通りです!
「差集め算」の核心は、この図にあるように、買った個数が同じということですね。
ただ、小5(上)第3回の「割合の利用」で、マルイチ算をやりましたね。今回は、このマルイチ算でも解いていきます。

例題1をマルイチ算で解く
問題文をもう一度見てみましょう。


この問題では、「同じ数ずつ買った」というところに注目して、この数を①個とおきます。


そうすると、Aさんがはらった代金は、$\maruii{80}$ とおけますね。同じように、Bさんがはらった代金も<マル数字>で表してみましょう。


$\maruii{60}$ になるわ!

そうですね。これらを使って式を立てると次のようになります。


マル数字どうしを計算すると次のようになります。


⑳=180ですから、両辺を20で割って、①を求めます。


そうすると、AさんとBさんはそれぞれ9個ずつ買ったことになりますね。
でも、マルイチ算で解く必要があるのかしら。

「マルイチ算」の重要性
確かに、マルイチ算は一見すると難しいですよね。
今回の差集め算では、マルイチ算を使わないほうが早く解けるものもあれば、マルイチ算を使ったほうが早い場合もあります。
しかし、マルイチ算を使わないほうが早く解けるからといって、マルイチ算をまったく使わないのは賛成できません。理由は4つあります。
- マルイチ算は、差集め算の場合だけでなく、損益算や消去算や仕事算(ニュートン算)や、図形の分野でも使える「万能な武器」です。いろんなパターンを覚えるより、マルイチ算で串刺しにしたほうが思考経済上有利です。
- 難しい問題の中には、マルイチ算を使った方が、反射的に早く解けるものが多くあります。また、マルイチ算の計算方法は慣れてしまうとスラスラできるようになりますので、図を書くより時間短縮になります。
- マルイチ算で方程式の思考方法を身につけておくことは、中学校以降の勉強にプラスになるし、実際、答えが必ず出るので、アタマの回転も速くなります。
- 算数が得意になる鉄則は「5回解くより5通りで解け」です。安易な暗記ではなく、試行錯誤を重ねるからこそ、学力が伸びます。別解としてマルイチ算を使えるときは、積極的に取り組みましょう。

ずいぶんアツくなってますね!

はい。実は、今回の差集め算の問題は、すべてマルイチ算で解けますので、マルイチ算が使えるようになる「大チャンス」なんです。
ここを4年のままの思考でスルーしちゃうと、思考が4年のままになってしまいます。ですので、今回のすべての問題をマルイチ算で解いておくべきだと思います。
【例題2】以降も、マルイチ算の別解を解説しますので、まずは、下の練習問題で、マルイチ算の計算を身につけてください。
マルイチ算練習問題 (1434 ダウンロード )
予習シリーズ算数 いろいろな差集め算 例題2
例題2の解き方
【例題2(1)】の問題を見てみましょう。


これは典型的な「過不足算」ですね。【例題1】と同じ図を書きましょう。

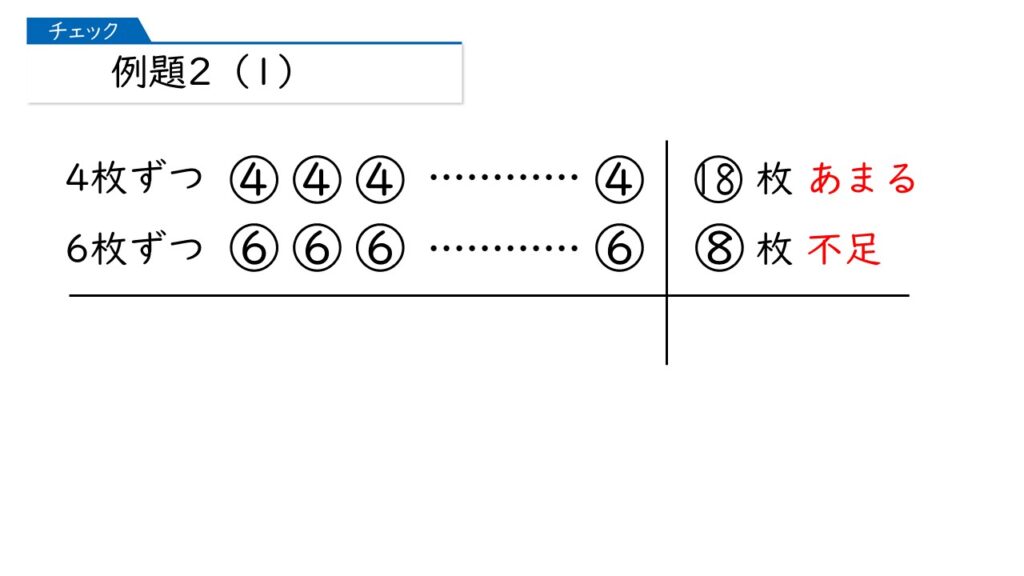
この図では、上が「18枚あまる」、下が「8枚不足」になっています。このように「あまると不足」の場合、全体の差は「あまる数と不足する数の合計」になります。
つまり、「上(実際に配った枚数)は、用意した枚数より18枚少ない」、「下(配ろうとした枚数)は、用意した枚数より8枚多い」ので、用意した枚数を基準にすると、上(実際に配った枚数)は下(配ろうとした枚数)より18+8=26枚少ない、ということです。


全体の差である26枚は、一人ずつの枚数の差が積み上がったものです。


これで解けますね。


子どもの人数は、26÷2=13人だから、用意した折り紙の枚数は 4×13+18=70枚ね。

正解です! では次に、【例題2(2)】の問題を見てみましょう。


例題2(1)と同じく、図で整理してみましょう。


この図では、上が「40個あまる」、下が「8個あまる」になっています。このように「あまるとあまる」の場合、全体の差は「あまる数どうしの差」になります。
つまり、上も下も「実際に配った枚数」を表していますから、残った枚数の差が全体の差になります。


全体の差である32個は、一人ずつの個数の差が積み上がったものです。


これで解けますね。

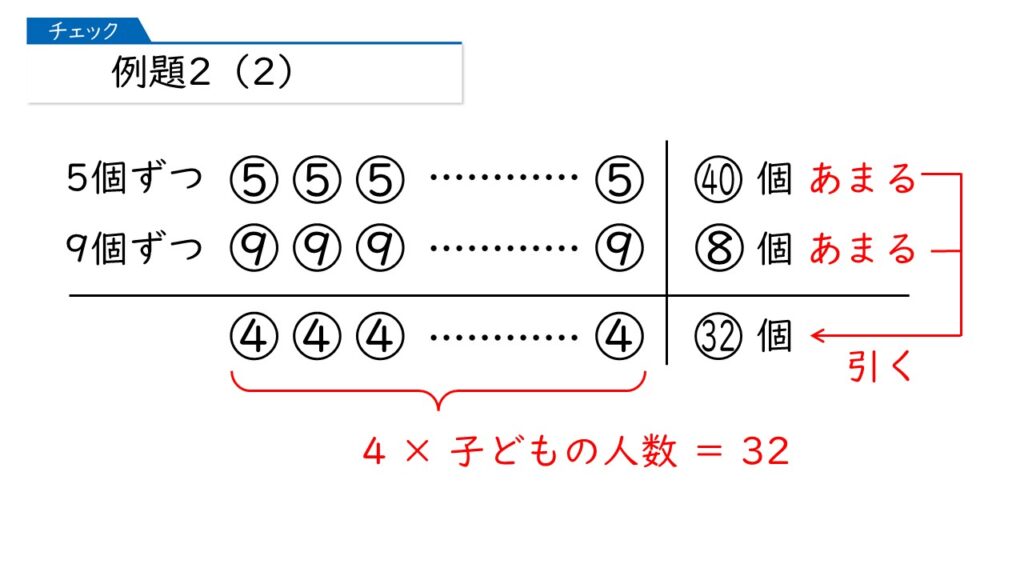
子どもの人数は、32÷4=8人だから、用意したアメの個数は 5×8+40=80個ね。

正解です! では次に、【例題2(3)】の問題を見てみましょう。


例題2(2)と同じく、図で整理してみましょう。

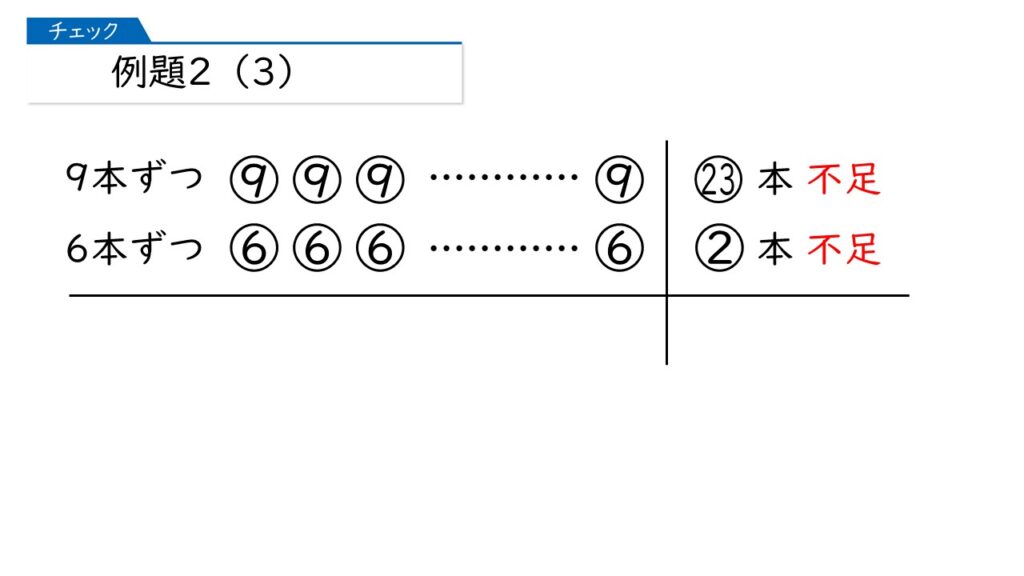
この図では、上が「23本不足」、下が「2本不足」になっています。このように「不足と不足」の場合、全体の差は「不足する数どうしの差」になります。

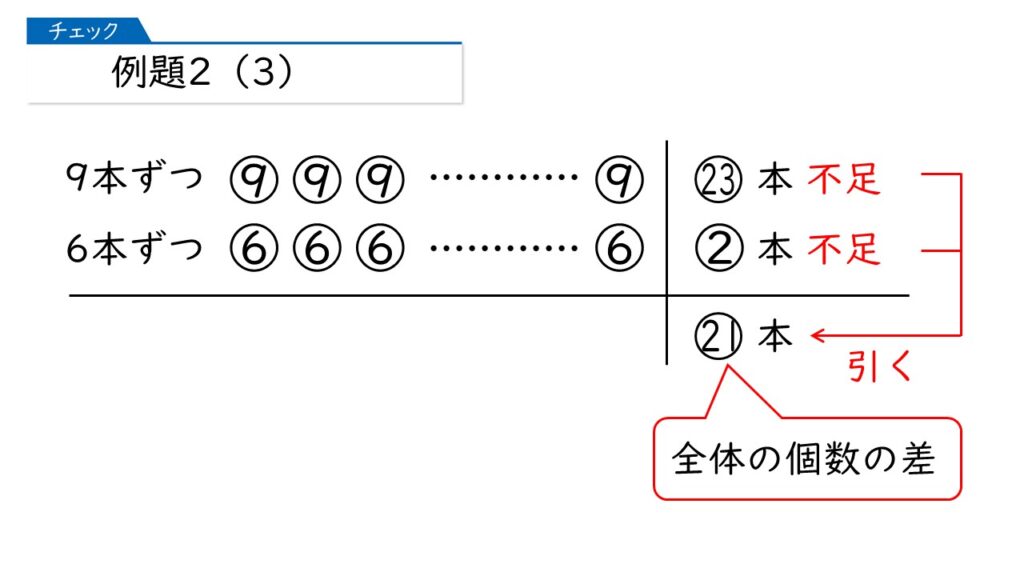
全体の差である21本は、一人ずつの個数の差が積み上がったものです。

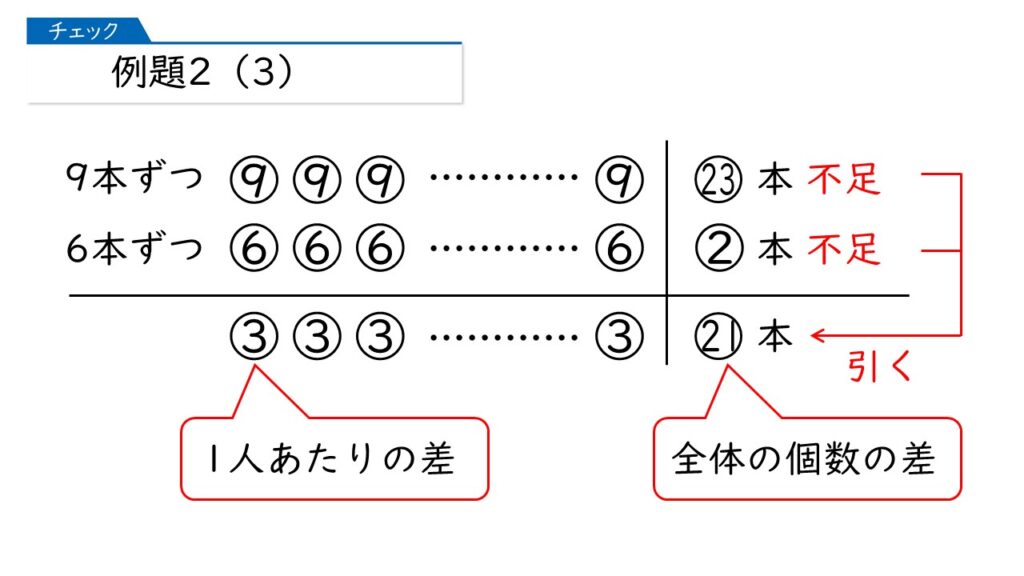
これで解けますね。

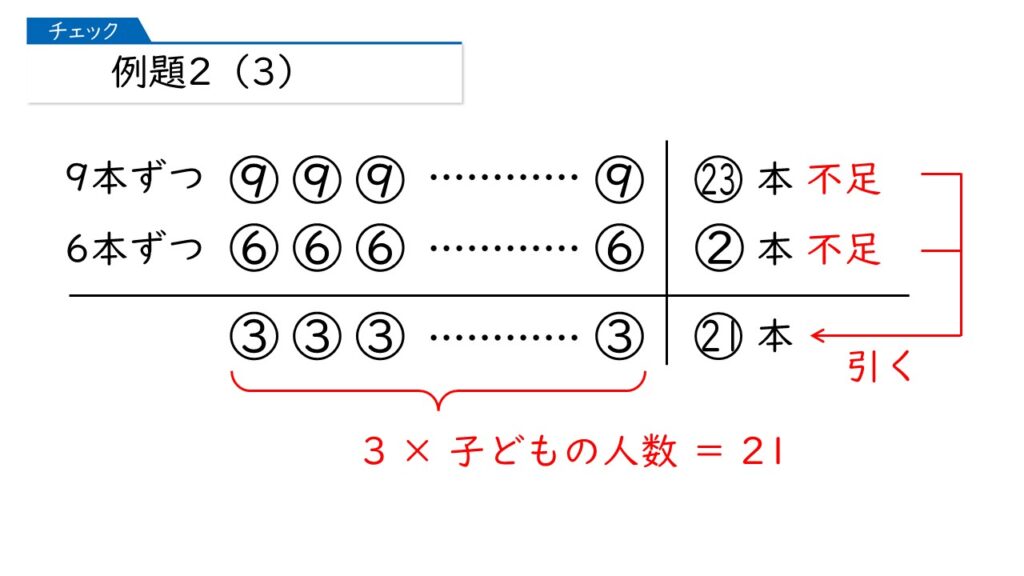
子どもの人数は、21÷3=7人だから、用意したえんぴつの本数は 9×7-23=40本ね。

正解です!

例題1をマルイチ算で解く
さぁ、マルイチ算に挑戦してみましょう! まずは、【例題2(1)】です。例題2では、子どもの人数を①とおきます。


次に、①を使って、用意した折り紙の枚数を表します。


ここで、4×①=④と計算しましょう。


用意した折り紙の枚数を、さらに残りの条件を使って表します。


これで、用意した折り紙の枚数を2通りで表しましたので、これをイコール(=)で結んで解きます。


これをどのようにして解けばいいでしょうか。

ダウンロードした練習問題でやったわ。両辺から「小さい方のマル数字」、この式では④を引けばいいのね。


そうです! すると、何から8を引けば18になるかを考えて、②を求めましょう。


②=26になるわ。

そうですね。そうしたら最後に、両辺を2で割って、①を求めましょう。


なるほど! 確かに、子どもの人数が13人になったわ。

では【例題2(2)】をやってみましょう。ここでも、子どもの人数を①とおきますよ。


では、①を使って式を立ててみましょう。

用意したアメの個数は、「1人に5個ずつ配ると40個あまる」から、「⑤+40」ね。


その通りです! 用意したアメの個数を別の式で表すとどうなりますか。

「1人に9個ずつ配ると8個あまる」から、⑨+8ね。


そうですね! 用意したアメの個数を2通りで表しましたので、これをイコール(=)で結んで解きましょう。


両辺から「小さい方のマル数字」、この式では⑤を引けばいいのね。


よくできました! ここまでくれば、もう大丈夫ですね。


④=32だから、両辺を4で割って、①=8人ね。


慣れてきましたね!

では【例題2(3)】をやってみましょう。ここでも、子どもの人数を①とおきますよ。


では、①を使って式を立ててみましょう。

用意したえんぴつの本数は「⑨-23」と「⑥-2」で表すことができるわ。


そうですね! ではこの2つをイコールで結んで解きましょう。


カンタンだわ。両辺から「小さい方のマル数字」、この式では⑥を引けばいいのね。


あれっ、マイナスが出てきたわ。小学生は負の数を習わないから解けないんじゃないかしら。

いえいえ、次のようにすれば解けますよ。


なるほど! そうすれば、③=21になるのね。


ここまでくれば、もう大丈夫ですね。


確かに、子どもの人数が7人になったわ。慣れれば、そんなに難しくないかも知れませんね。

そうなんです! 【例題3】以降も、マルイチ算で解けるようにすると、問題のいろいろなパターンに振り回されなくなりますよ。

予習シリーズ算数 いろいろな差集め算 例題3
例題3の解き方
下の問題文の赤字のところに注目です。


【例題2】と同じように、図に整理しましょう。上と下で、少ない方の個数にそろえて書くことがポイントです。

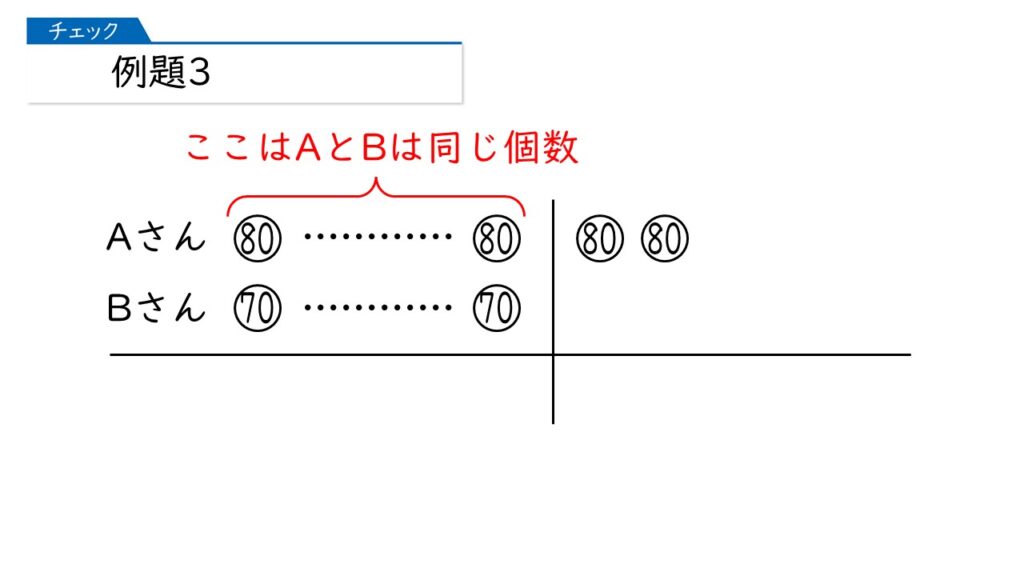
次に、下の問題文の赤字のところに注目してください。


下の図のように整理すると、全体の差と、1個あたりの差が分かりますね。


そうすると、何が求まりますか?

Bさんが買った個数ね。

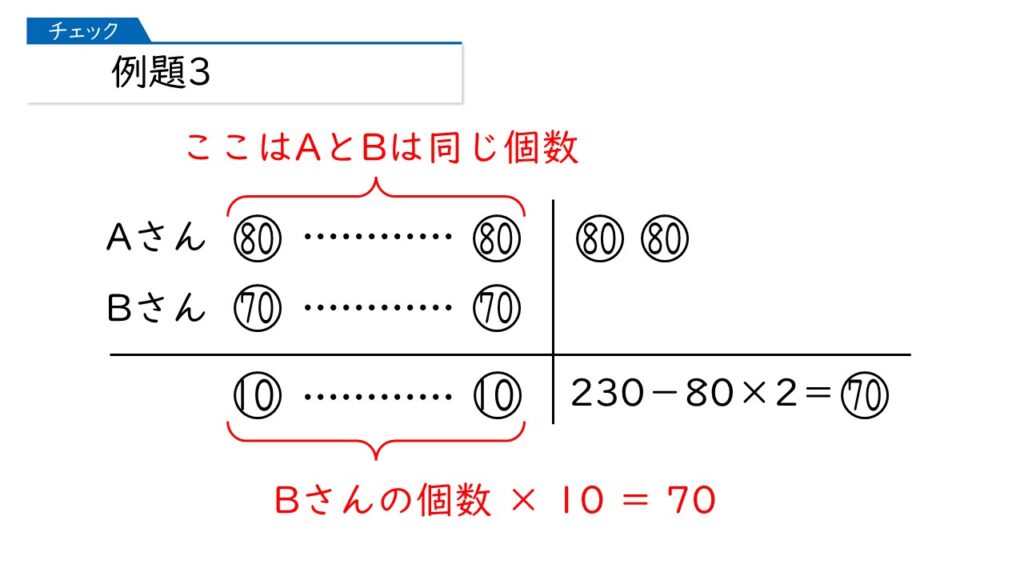
その通りです! Bさんは、70÷10=7個買いましたね。だから、Aさんは7+2=9個買ったことになります。
ここは、別の見方もできます。下の図を見てください。

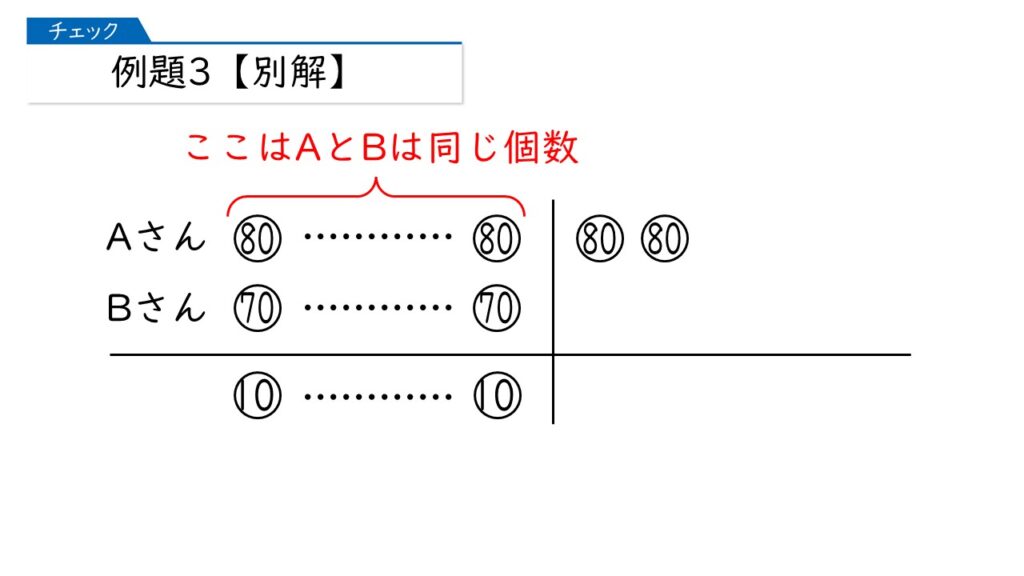
AさんがBさんよりも多くはらった230円は、この図ではどこになりますか? それが分かれば式が立ちます。

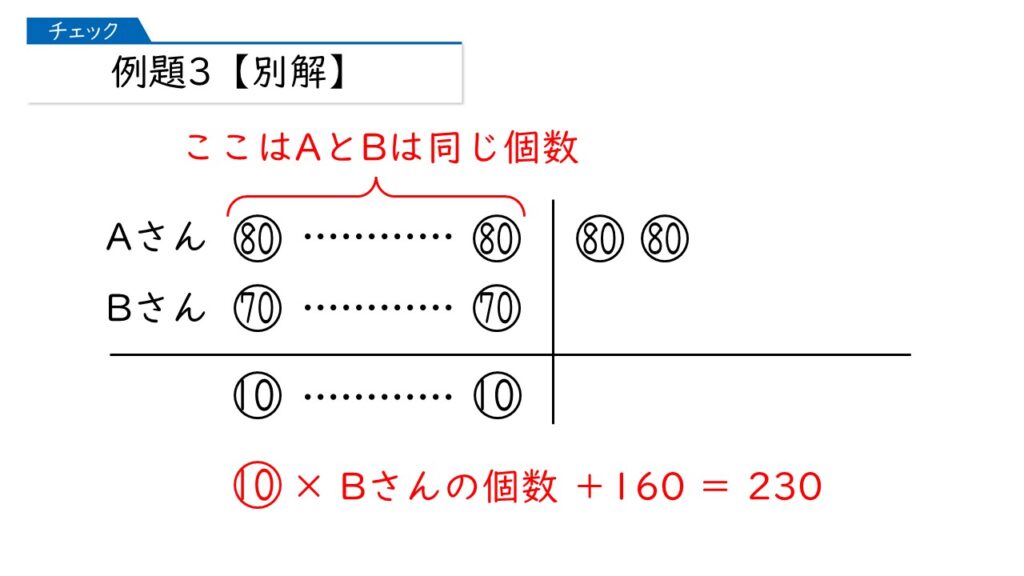
なるほど! この式を解くと、Bさんが買った個数が、(230-160)÷10=7(個)になるわ。

例題3をマルイチ算で解く
問題の赤字のところに注目して、何を①と置くかを考えましょう。


むむむ…、難しいわ。

大丈夫! 初めは難しいくて当然です。まずは、真似てください。
次のように、少なくもらった方、つまりBさんが買った個数を①とおくと、Aさんが買った個数が(①+2)個になります。


次に、問題文に「Aさんがはらった代金はBさんがはらった代金yほりも230円高い」とありますので、①を使って次のように式を立てます。


式の中にカッコがあったら、分配法則を使ってバラします。


分配法則とは、「80×(①+2)=80×①+80×2」のように計算することです。すると、下の図のようになります。


もう解けるわ。両辺から $\maruii{70}$ を引けばいいのね!

その通りです!


予習シリーズ算数 いろいろな差集め算 例題4
例題4の解き方

問題文を読んで、【例題3】と同じ図を書いてみましょう。


これって、【例題2】でやったものですよね!

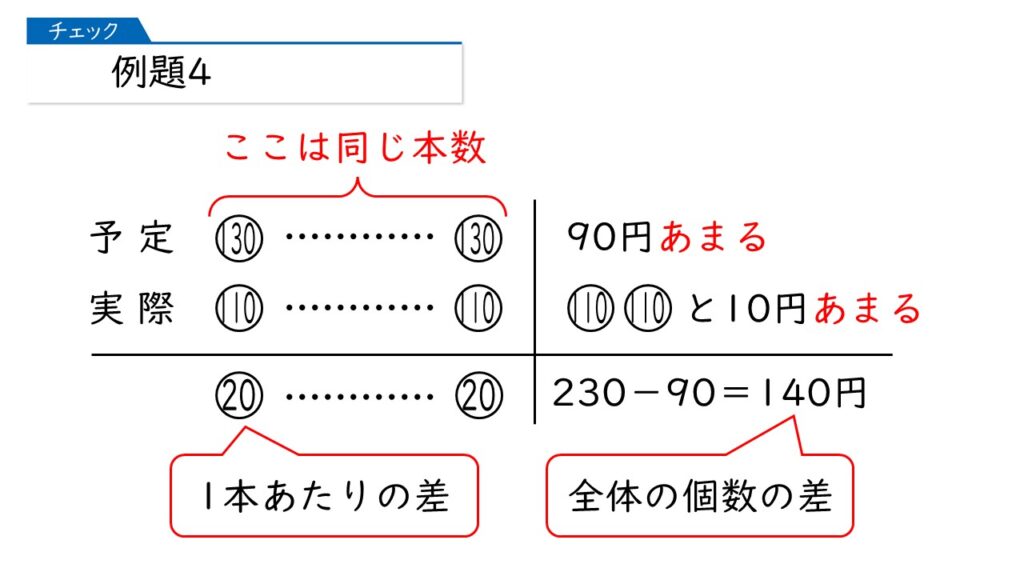
そうだんです。だから、【例題2】と同じように解けばいいんですね。

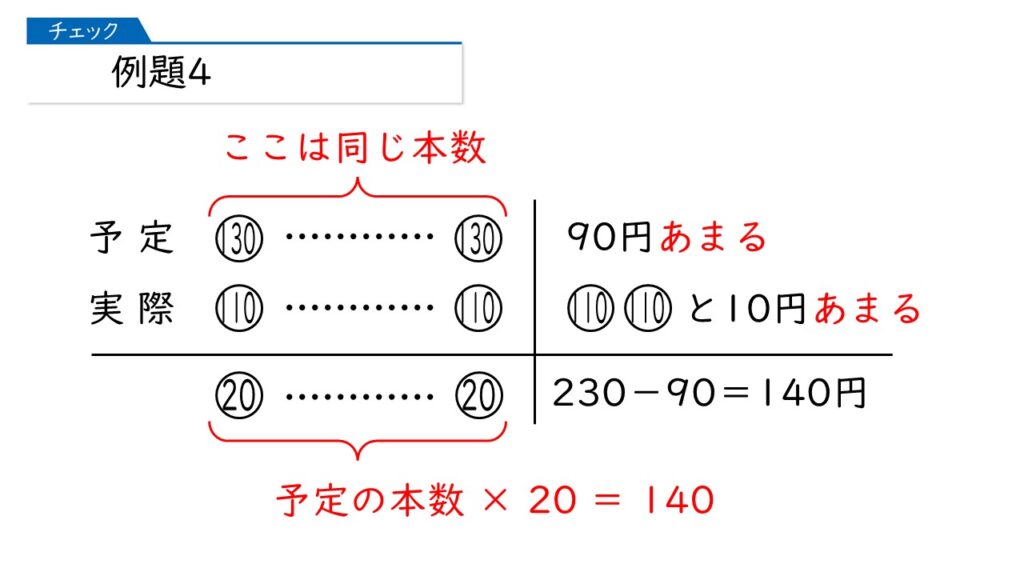
そうすると、予定していた個数は、140÷20=7本ね。そうすると、Aさんがはじめに持っていたお金は、130×7+90=1000円!

正解です!

例題4をマルイチ算で解く
では、【例題4】をマルイチ算で解いてみましょう。問題文の赤字のところに注意すると、何を①とおけばいいでしょうか。


予定していた本数を①とおけばいいのね。

はい、その通りです! 慣れてきましたね。


では、問題文にしたがって、式を立てましょう。


ここで、「分配法則」を使って、カッコを取ります。


220+10は計算できますね。

はい、できます。


両辺から $\maruiii{110}$ を引けば、⑳+90=230 になるから、⑳=140 ね。すると ①=7、つまり、予定していた本数が7本になるわ!

良かったです! マルイチ算に慣れると、必ず答えがでますね。

予習シリーズ算数 いろいろな差集め算 例題5
例題5の解き方

これは【例題3】と同じ問題ですので、同じ図を書きましょう。「少ない方の個数にそろえる」のがコツですよ。


この問題のポイントは、Aさんの所持金変わらないから、「上の段のお金の合計」と「下の段のお金の合計」は等しい、ということです。


なるほど。50×8+20=420円が、ミカン7個分の値段と同じになるのね! (1)の答えは420円だわ。

その通りです! これで(2)の答えもでますね。

ミカンで考えて、(420÷7)×15=900円ね。

大正解です!

例題5をマルイチ算で解く
では、マルイチ算に挑戦してみましょう。問題文の赤字のところに注意すると、何を①とおけばいいでしょうか。


ミカン1個の値段か、リンゴ1個の値段ですね。ミカン1個の値段のほうがリンゴ1個の値段より安いから、ミカン1個の値段を①とおくのがいいのね。

コツがつかめてきましたね! まったくその通りです。


では、式を書いて解いていきましょう!


⑦=420だから、①=60ね。つまり、ミカン1個の値段が60円ね。そうすると、(2)が60×15=900円って、カンタンに求まるわ。

大正解です、おめでとうございます!

サラサラ解けるとうれしいわ!

予習シリーズ算数 いろいろな差集め算 例題6
例題6の解き方
あと2題です、がんばりましょう!
【例題6】は特徴的な問題ですね。問題文の赤字のところから、何が分かりますか?


買う枚数を逆にすると、合計の金額が変わるってことね。

するどい、その通りです! 合計金額が安くなったということは、「予定では80円切手の枚数の方が多かった」わけです。


このことを前提に、図を書いてみましょう。


予定では、50円切手と80円切手のどちらかの枚数が多いはずね。その多かった分の枚数が、この図の真ん中の部分ということですね。

そうです。だから、この図の真ん中の枚数分の差を集めたものが180円ということになります。


なるほど。予定では80円切手の枚数の方が50円切手の枚数が多かったので、その多かった分の枚数が6枚になるのね。

その通りです! では、この図の左と右の部分の枚数は何枚になりますか?


「予定と実際の合計の枚数は同じ」で「差がでないところの枚数は同じ」だから、この図の左と右の部分の枚数は同じになるのね。
だから、実際に買った50円切手は13枚、80円切手は7枚になるわ。

そうですね、よくできました!

例題6をマルイチ算で解く
では、マルイチ算でも解いてみましょう。
実際買った50円切手を①枚、80円切手を(20-①)枚として、予定していた代金の合計と、実際にかかった代金の合計を表してみましょう。


次に、問題文にこれらの式をあてはめます。

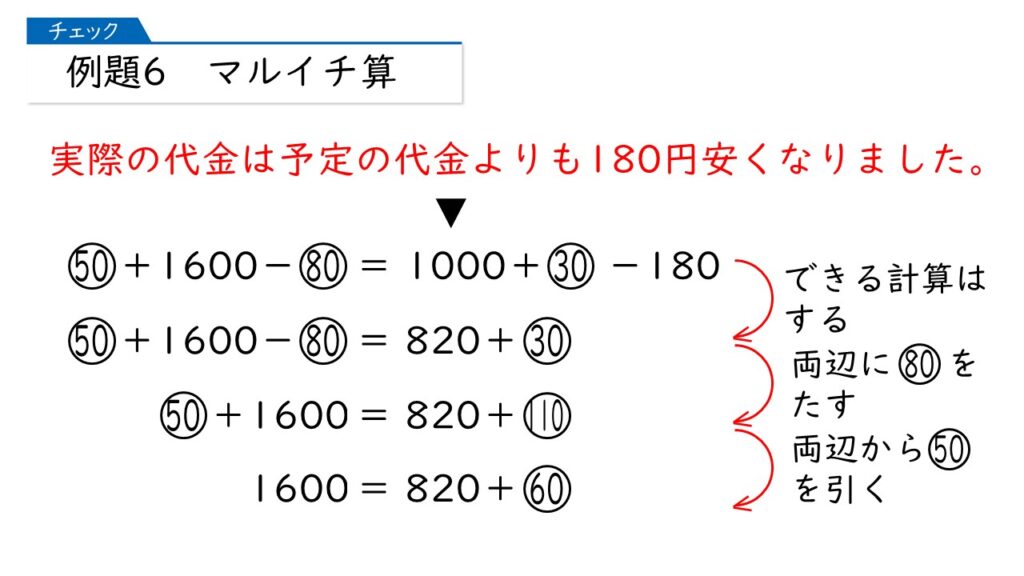
そうすると、①=13枚って求まるのね。でも、これは相当めんどくさくないですか?

確かに、かなりめんどくさいです。この問題は、かんたんな解法が分かっていればそれでやった方がいいですね。
ただ、差集め算にはいろんなパターンがあって、それらのパターンをいちいち覚えるというのは現実的ではありません。
特に、この【例題6】は、四谷大塚の模試には出るかもしれませんが、入試に出ることはほとんど考えられません。化石のような問題ですから。
ですので、入試本番での変化球に対応するという意味で、マルイチ算のトレーニングをしてください。

分かったわ。暗記ではなくて、実力で勝負すべきということね!

予習シリーズ算数 いろいろな差集め算 例題7
例題7の解き方

まず、上の問題文の赤字のところに注目して、図に表してみましょう。


「少ない人数でそろえる」のがポイントですね。さらに、まず、下の問題文の赤字のところに注目して、同じように図に表してみましょう。



そすると、次のことが分かります。

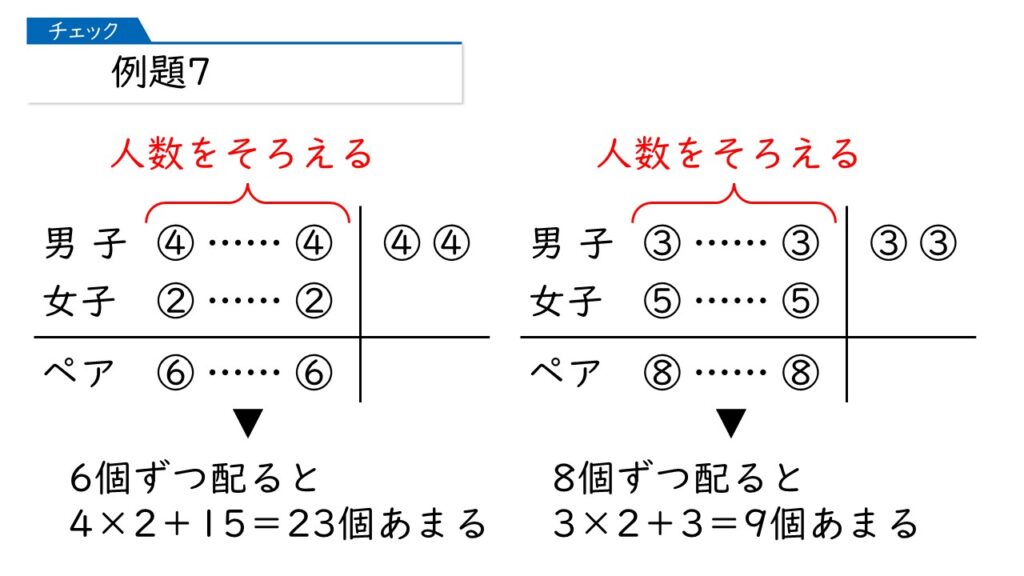
なるほど。そうすれば【例題2】と同じように解けるんですね!

よく気づきました。その通りです!「男子4人と女子2人のペアをペアにして配った場合」と、「男子3人と女子5人をペアにして配った場合」として考えるわけです。


そうすると、ペアの数は、14÷2=7(組)ね。そうすると、アメの個数は、6×7+23=65個になるわ。

その通りです、正解です!

例題7をマルイチ算で解く
さぁ、次はマルイチ算で解いてみましょう。問題文の赤字のところに注目すると、何を①とおけますか。


女子の人数が男子の人数より少ないから、女子の人数を①とおくといいわ。


さすがです! 女子の人数を①人、男子の人数を(①+2)人とおいて、式を立てましょう。


そうすると、②=14だから、①=7、女子が7人ということね。男子は女子より2人多いから、9人。
すると、アメの個数は、4×9+2×7+15=65個になったわ。
マルイチ算で解けば、男女をペアにする必要もないわ。

そうなんです。
問題文を見たときに解き方がひらめかなかったときは、マルイチ算に持ち込んで答えをひねり出す、というスタンスをとるのがいいですね。
サピックスの上位生は、図ではなくマルイチ算で解いていますので、マルイチ算でも解けるようにして欲しいところです。

わかったわ、そうしてみます。

マルイチ算のいろいろなパターンの練習問題<ダウンロード>
予習シリーズの差集め算の例題をみてきましたが、差集め算にはもっとたくさんのバリエーションがありますので、ここまでの練習では本番で太刀打ちできません。

えっ、そうなの!

はい。ですので、入試を意識した練習問題を27題用意しました。ダウンロードして挑戦してみてください。マルイチ算での解法をつけてありますよ。
マルイチ算の応用問題 (1196 ダウンロード )
解法がのっていればできそうね。今日もありがとうございました!

いえいえ、こちらこそいつもお付き合いいただいてありがとうございます。ギモンや質問がありましたら、下のフォームからお願いします!



第8回.jpg)





[…] 四谷大塚 予習シリーズ 算数 徹底解説 5年上第4回 いろいろな差集め算-ア… […]