四谷大塚 予習シリーズ 算数 徹底解説 5年上第8回 多角形の回転・転がり移動－クイックラーニング
yamada
中学受験マスターガイド
四谷大塚 予習シリーズ 算数 徹底解説 5年上第9回 円の回転・転がり移動－クイックラーニング
yamada
記事内に商品プロモーションを含む場合があります
前回は「多角形」の回転・転がり移動でしたね。今回は「円」の回転・転がり移動です。
前回は「自分の手を使って、途中の過程を書く」ことがポイントだったわ。今回も同じなの？
はい、その通りです。予習シリーズは最後の結果だけが書かれた図をのせていますが、その図を覚えたとしても応用がききません。途中の図をしっかり書いていきましょう！
この記事の目次
予習シリーズ算数 円の回転・転がり移動 例題1
まず、例題1です。下の図1のように、直線ABを直径とする半円を、点Aを中心にして反時計回りに30度回転させました。
このとき、弧ABが動いたあとの図形を表したものが図2のぬられた部分です。このぬられた部分の面積は何cm2になりますか。
初めて見る形だわ…。どう解けばいいのかしら？
初めて見ると難しいですよね。下の図3と比べるとどうですか？
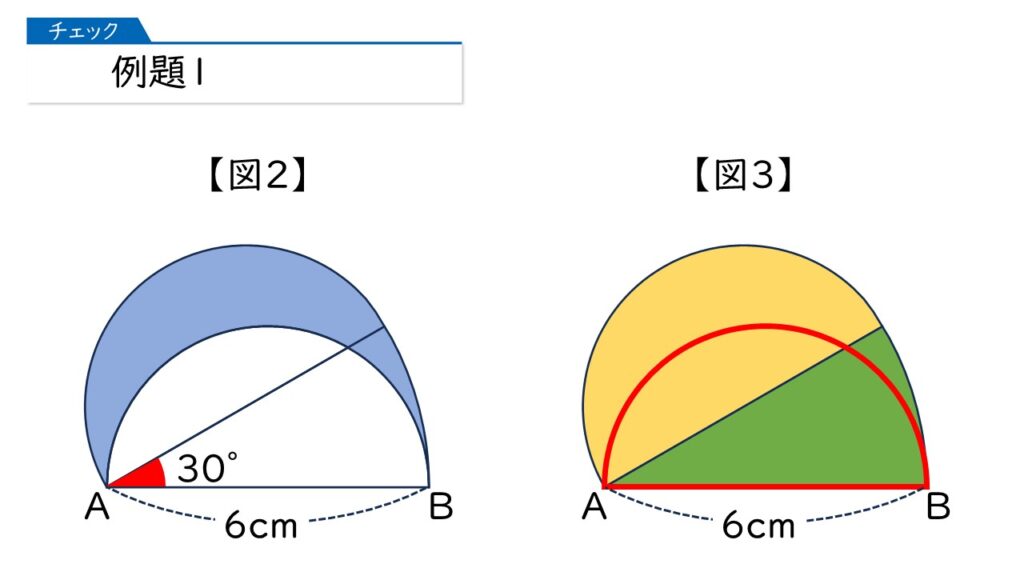
分かったわ。黄色の半円の面積と緑のおうぎ形の面積をたして、そこから赤の半円の面積を引けばいいのね！
その通りです！ 気づくのが早かったですね。黄色の半円と赤の半円の面積は同じですから、結局、緑のおうぎ形の面積を求めればそれが答えになります。
6×6×$\dfrac{30}{360}$×3.14＝9.42（cm2）が答えね。
はい、その通りです。では、30度ではなく、90°回転させたらどうなりますか？
これも同じことね。答えは、6×6×$\dfrac{90}{360}$×3.14＝28.26（cm2）ね。
その通りです。カンペキに理解しましたね！
予習シリーズ算数 円の回転・転がり移動 例題2
例題2（1）の解き方
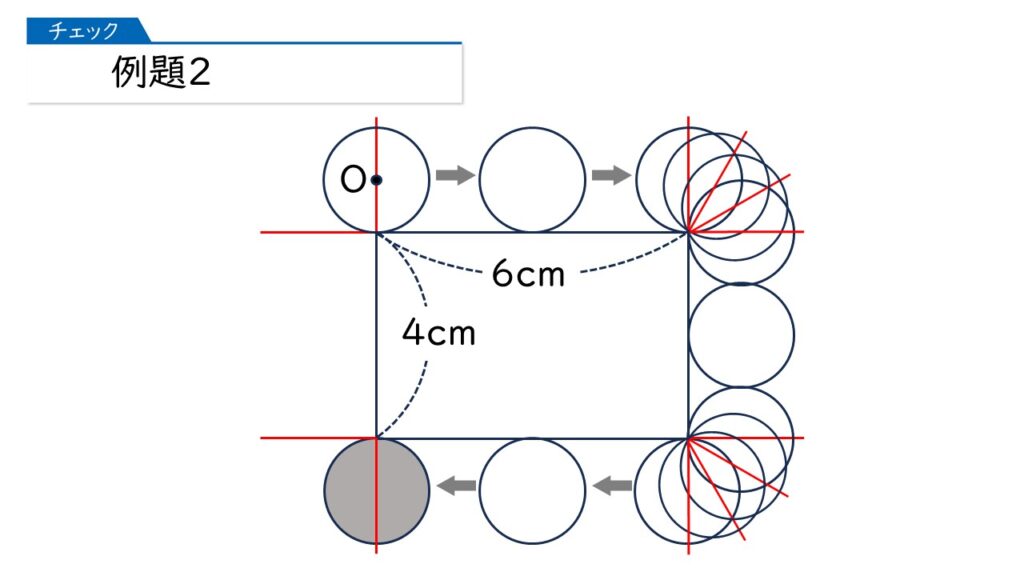
例題2に進みましょう。下の図のように、半径1cmの円が、長方形のまわりにそって転がりながら1周してもとの位置にもどります。このとき、円の中心Oが動いたあとの線の長さは何cmですか。
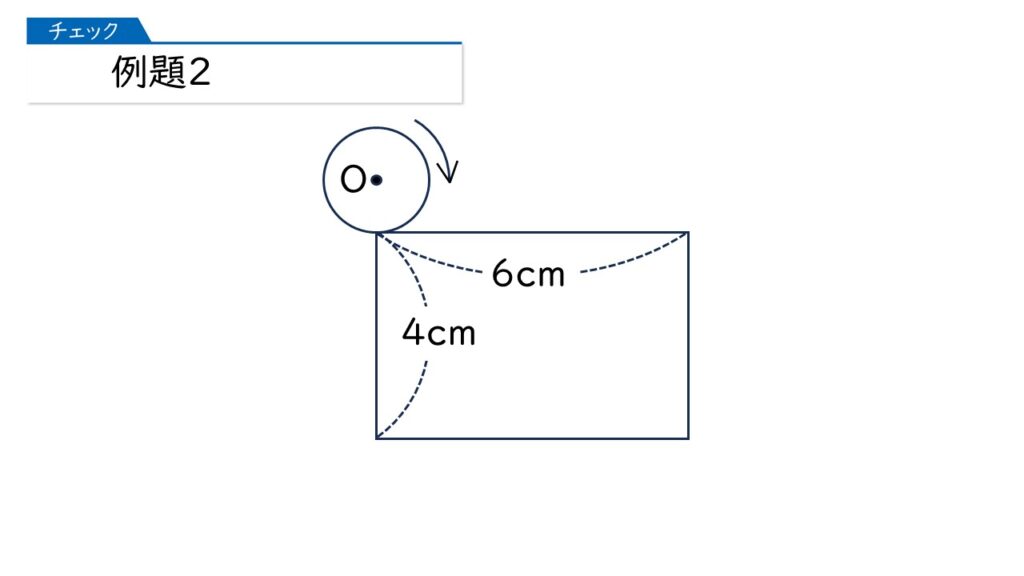
この問題を解くときには、ちょっとしたコツがあります。
円が1周するあいだに、「転がるところ」と「円周上の1点を中心に回転するところ」があります。この2つの部分の境目に、下の図のような補助線を書きます。
このような補助線を引いたあと、円をどんどん転がしていきます。
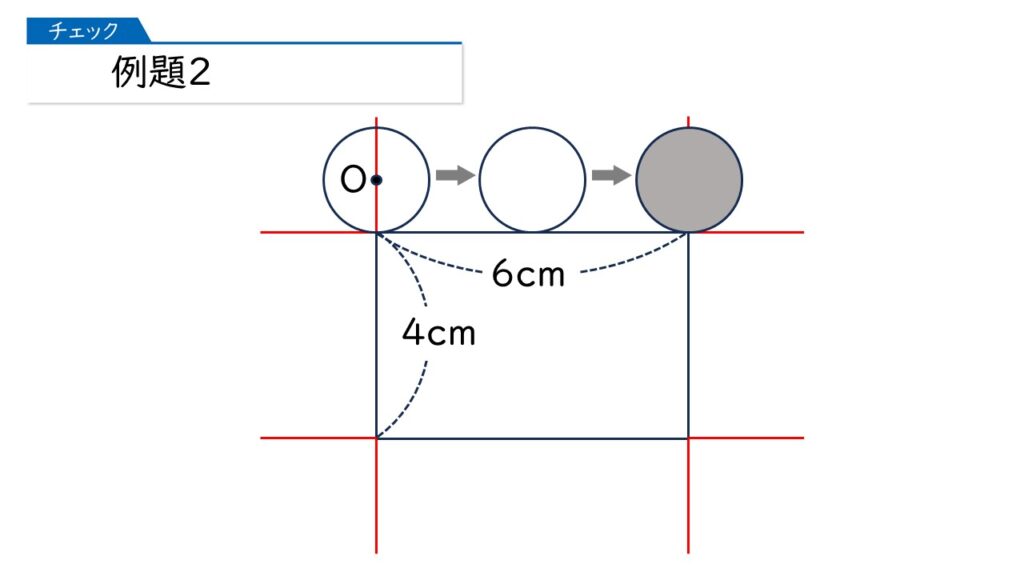
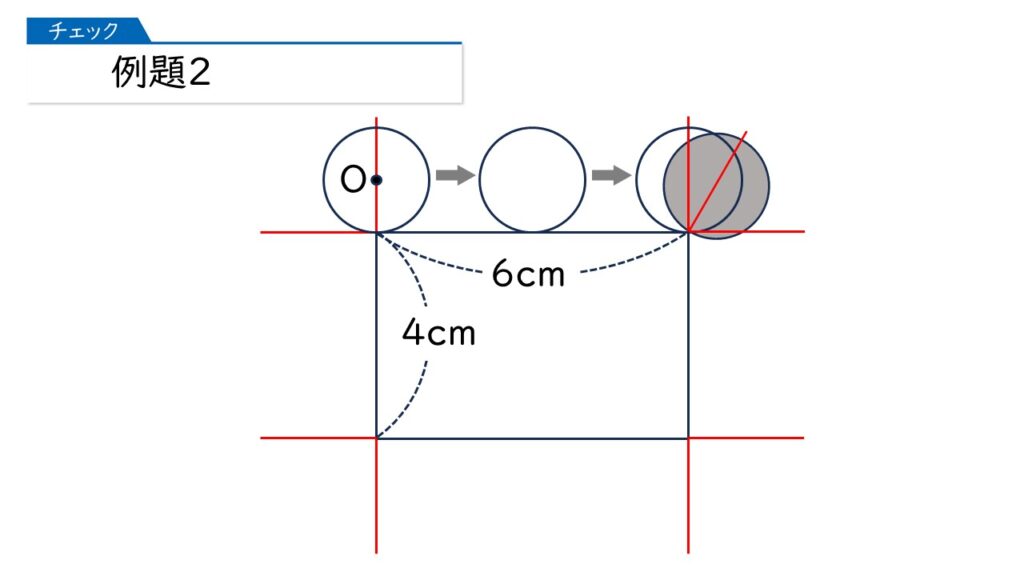
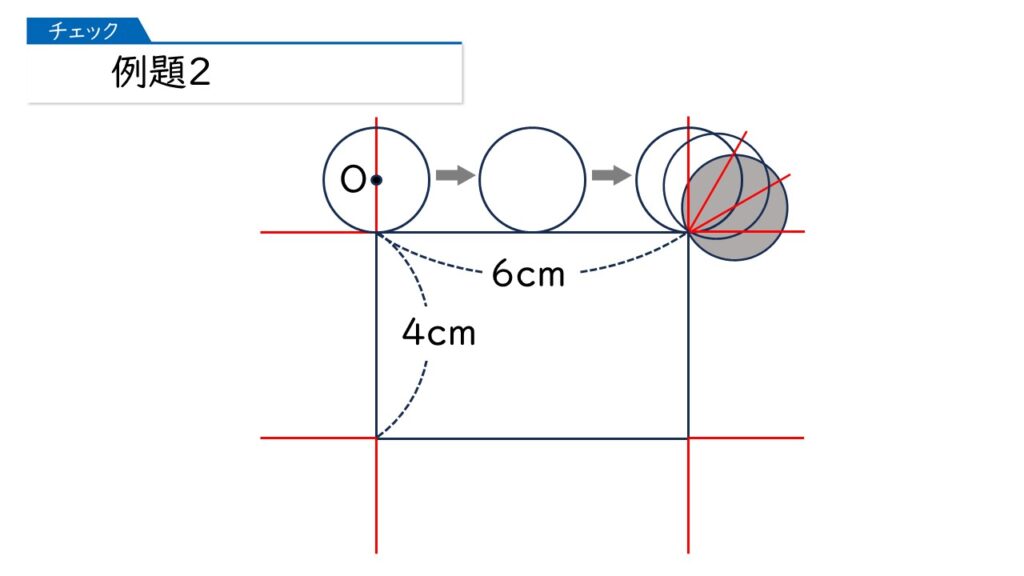
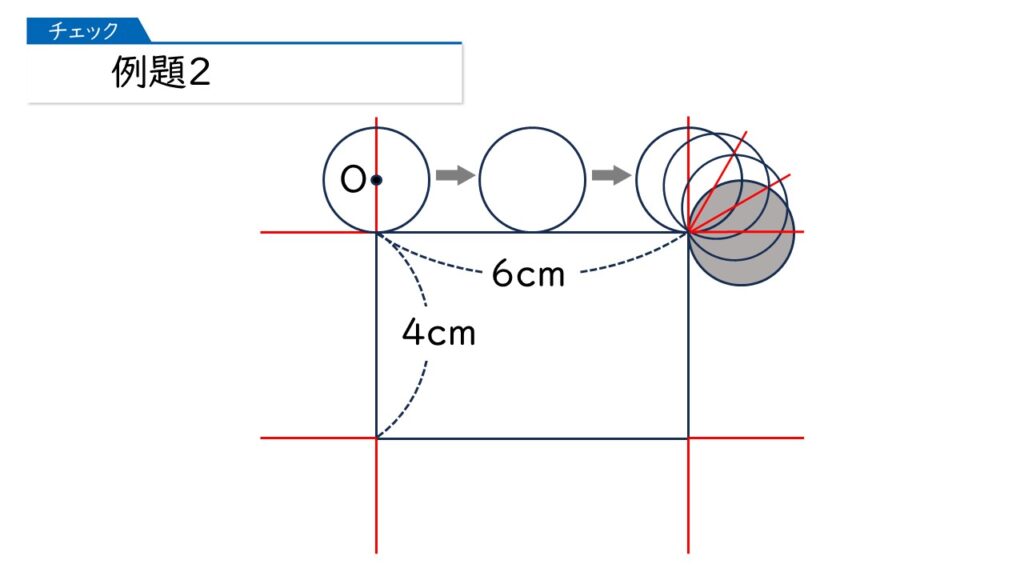
なるほど。長方形の直線部分では円は転がっていて、長方形の頂点のところで円は回転しているのね。
よく気づきました、その通りです。では、最後まで動かしてみましょう。
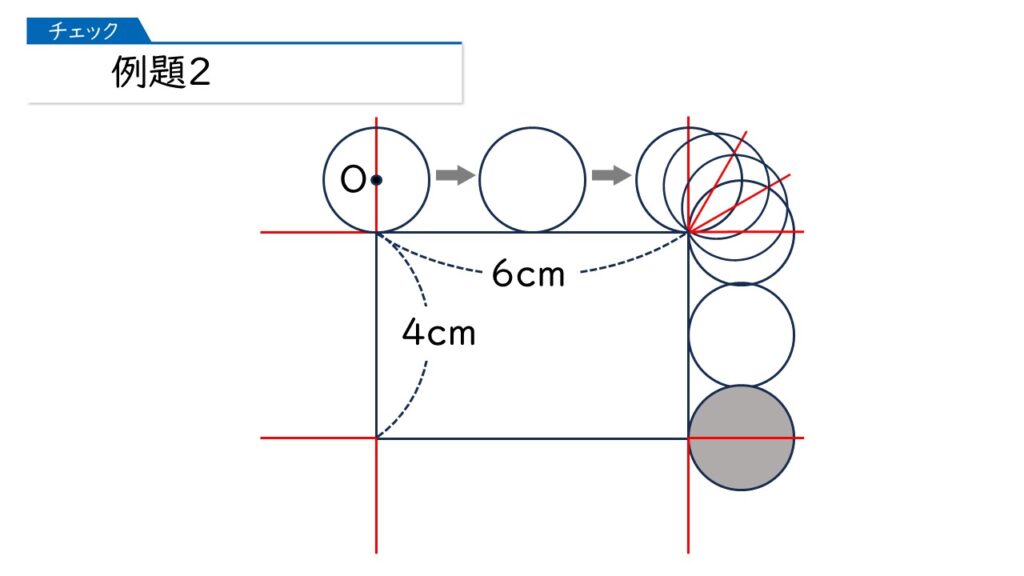
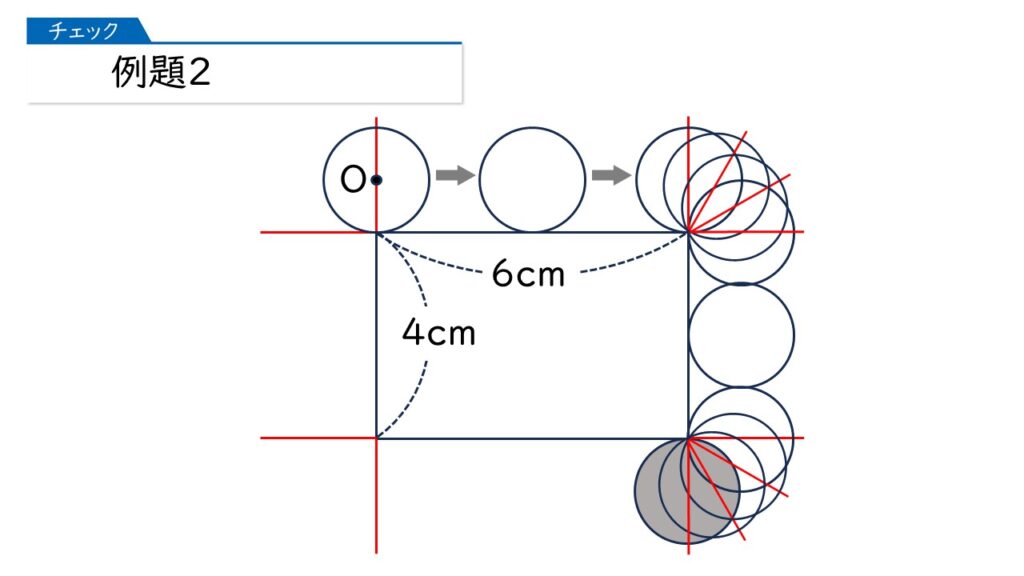
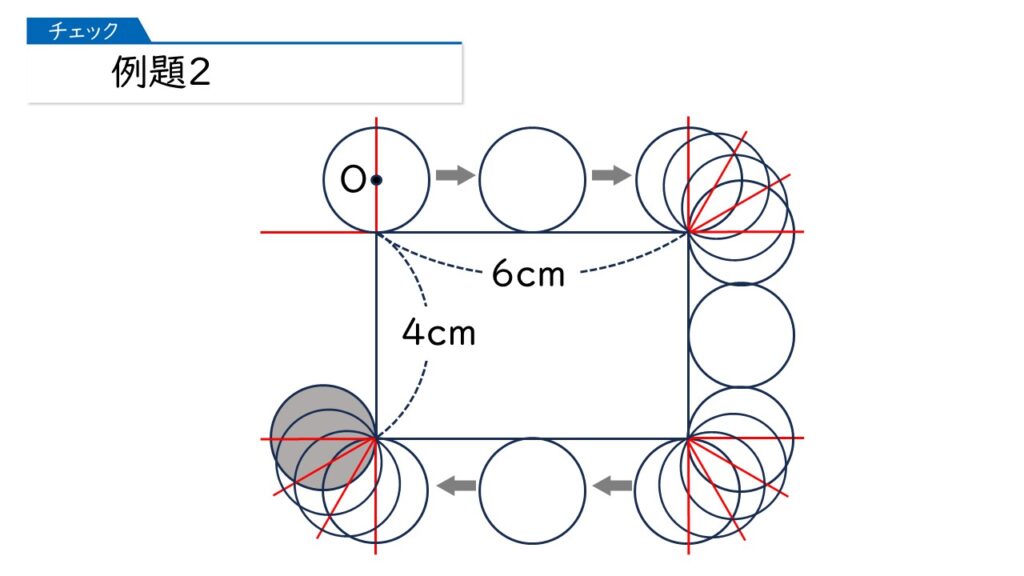
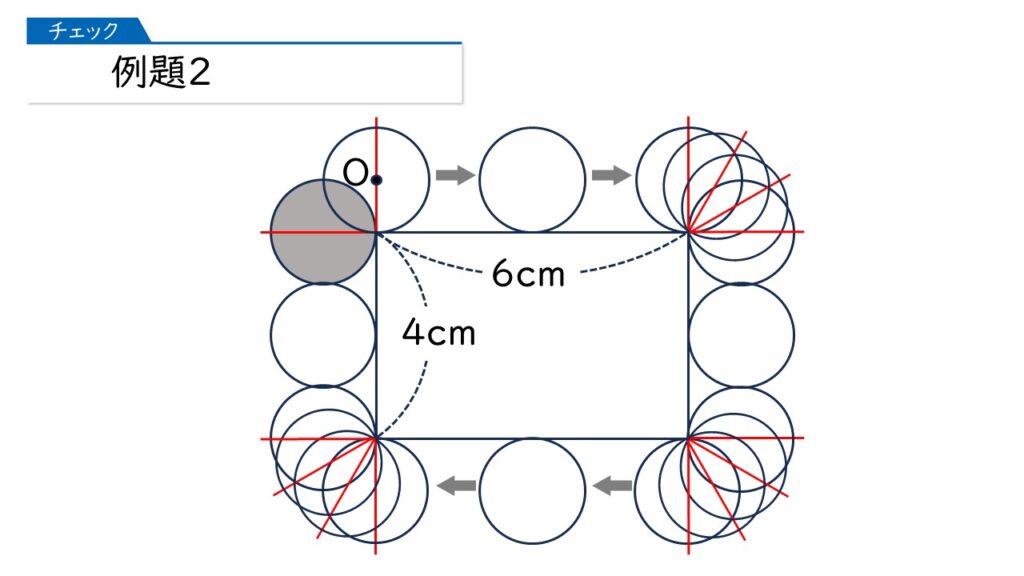
さあ、では（1）です。円の中心Oが動いたあとの線の長さは何cmになりますか？
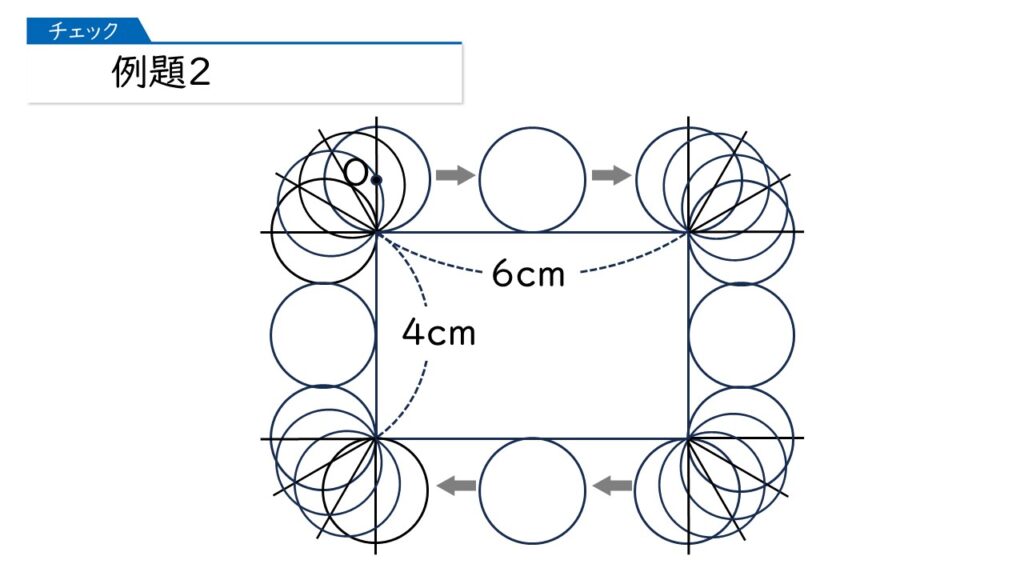
直線部分と曲線部分を合わせたものになるのね！
その通りです！ 上の図で、赤い曲線を全部つなげると円になることに気づけば、かんたんな式がたちますね。
1×2×3.14＋20＝26.28（cm）が答えね。
その通りです！
例題2（2）の解き方
次に（2）です。円が動いたあとの図形の面積は何cm2になりますか？
もう分かったわ。4つのおうぎ形の面積と4つの長方形の面積の和になるわ。
そうです！ 4つのおうぎ形をつなぎ合わせると1つの円になりますから、答えは次のようになります。
2×2×3.14＋2×20＝52.56（cm2）
1×1×3.14＋2×20にしちゃったわ。
よくあるまちがいですよ。（1）と（2）では、円の半径の長さがちがうところに注意が必要ですね。
予習シリーズ算数 円の回転・転がり移動 例題3
例題3（1）の解き方
例題3に進みましょう。下の図のように、半径2cmの円が、四分円のまわりにそって転がりながら1周してもとの位置にもどります。このとき、円の中心Oが動いたあとの線の長さは何cmですか。
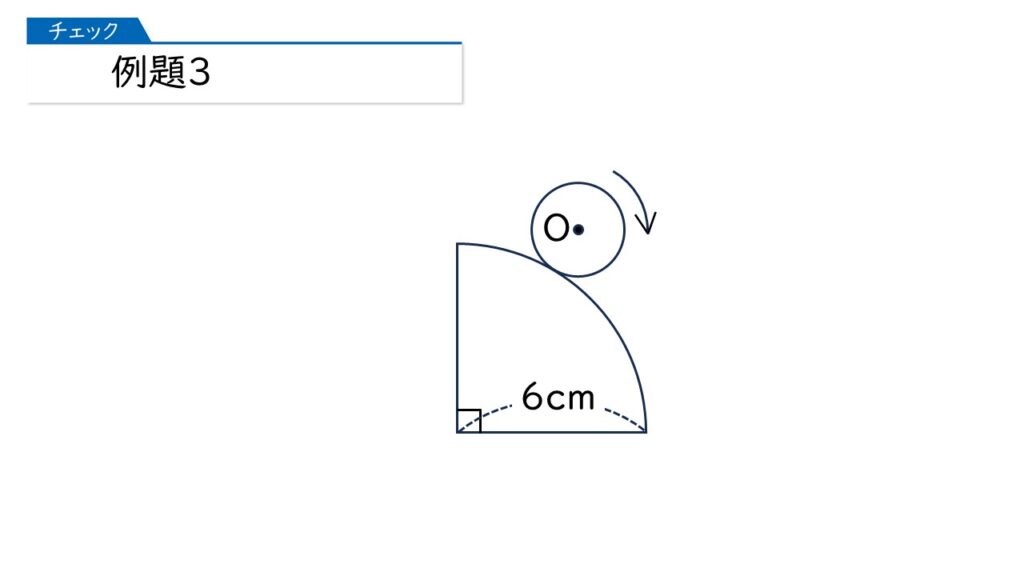
例題2で使ったコツをここでも使いましょう。
円が1周するあいだに、「転がるところ」と「円周上の1点を中心に回転するところ」があります。この2つの部分の境目に、下の図のような補助線を書きます。
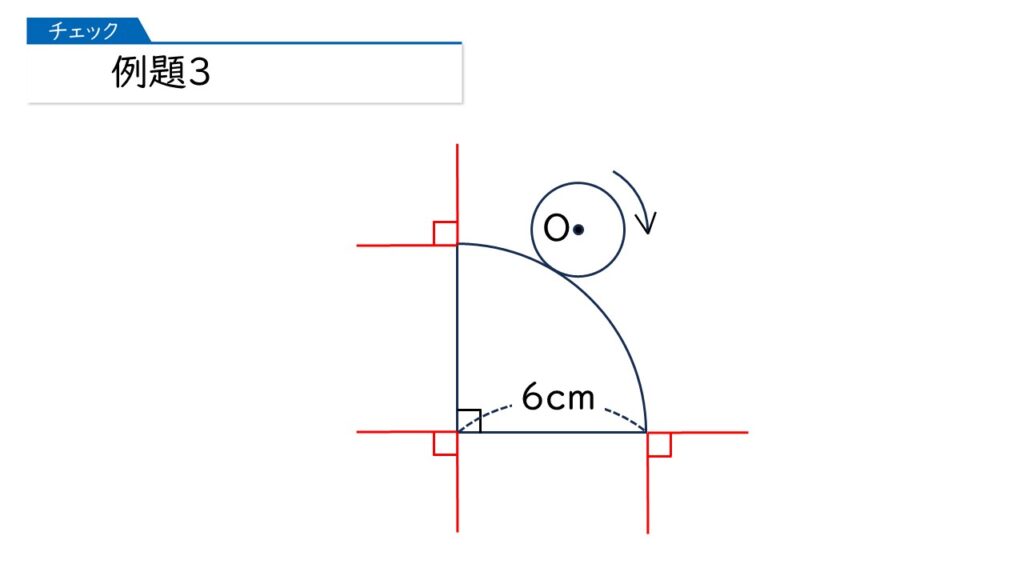
このような補助線を引いたあと、円をどんどん転がしていきます。
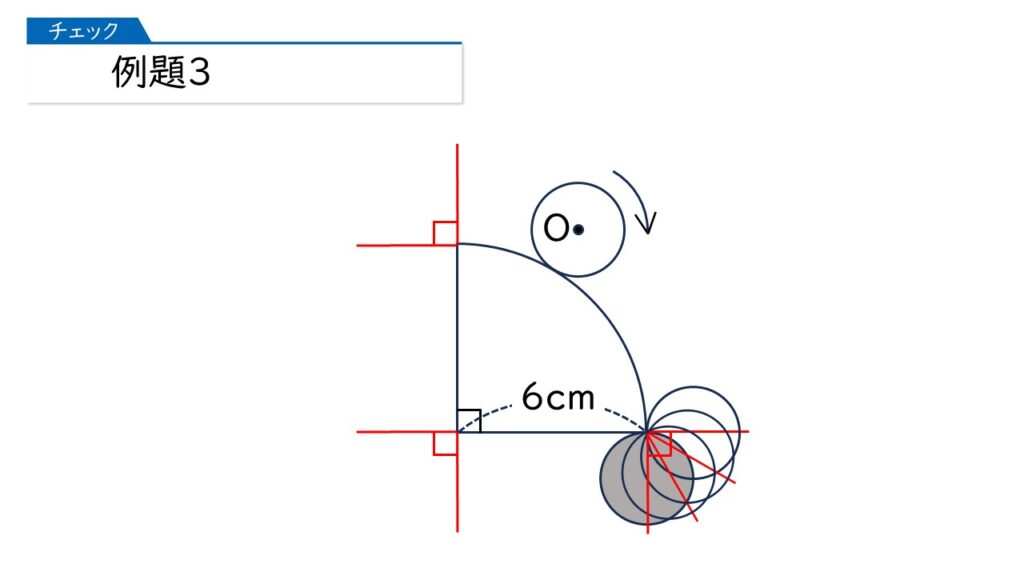
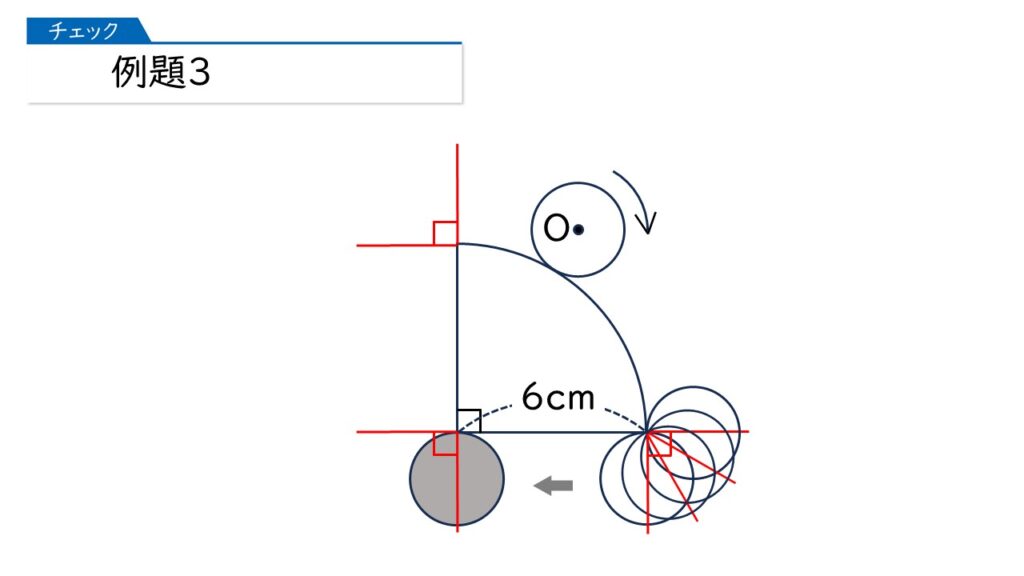
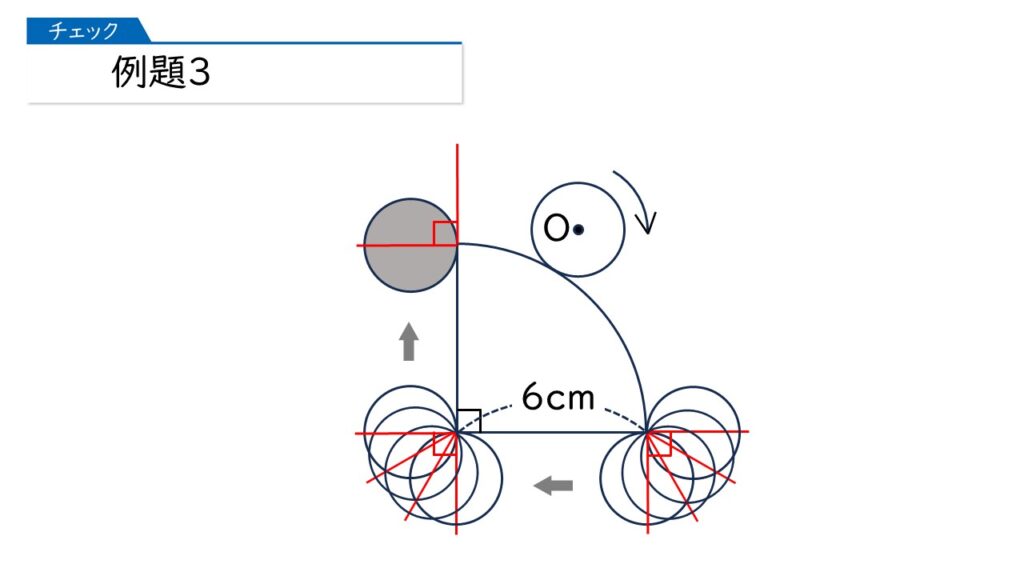
さあ、では（1）です。円の中心Oが動いたあとの線の長さは何cmになりますか？
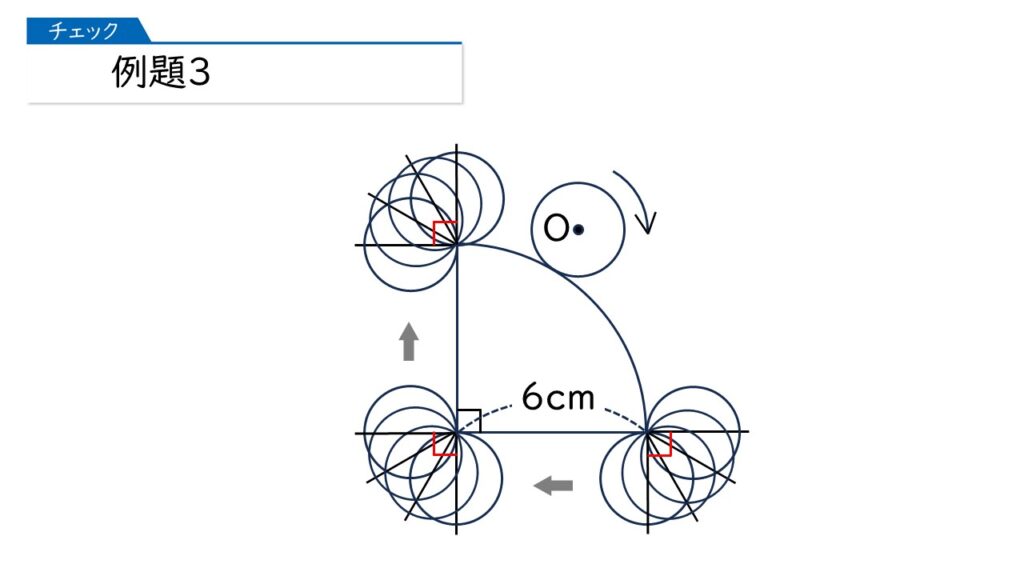
4つのおうぎ形の弧の長さと、2つの直線の長さの和になるのね。
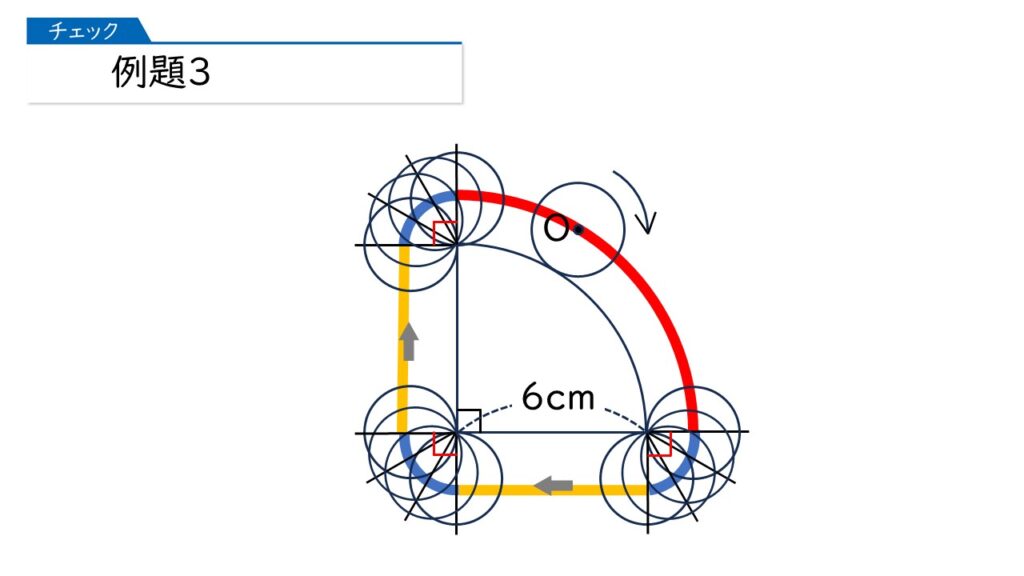
その通りです！ 赤の弧の長さと、青の弧の長さ×3と、黄色の長さ×2をたせばいいんですね。このとき、おうぎ形の半径の長さに注意が必要です。
今度はまちがえないわ。
16×$\dfrac{1}{4}$×3.14＋4×$\dfrac{3}{4}$×3.14＋12
＝(4＋3)×3.14＋12
＝33.98（cm）
これが答えね。
ご名答です！
例題3（2）の解き方
次に（2）です。円が動いたあとの図形の面積は何cm2になりますか？
おうぎ形の部分と長方形の部分は分かるわ。でも、右上の曲がっているところは難しいわ。
そうですよね。下の図を見てください。
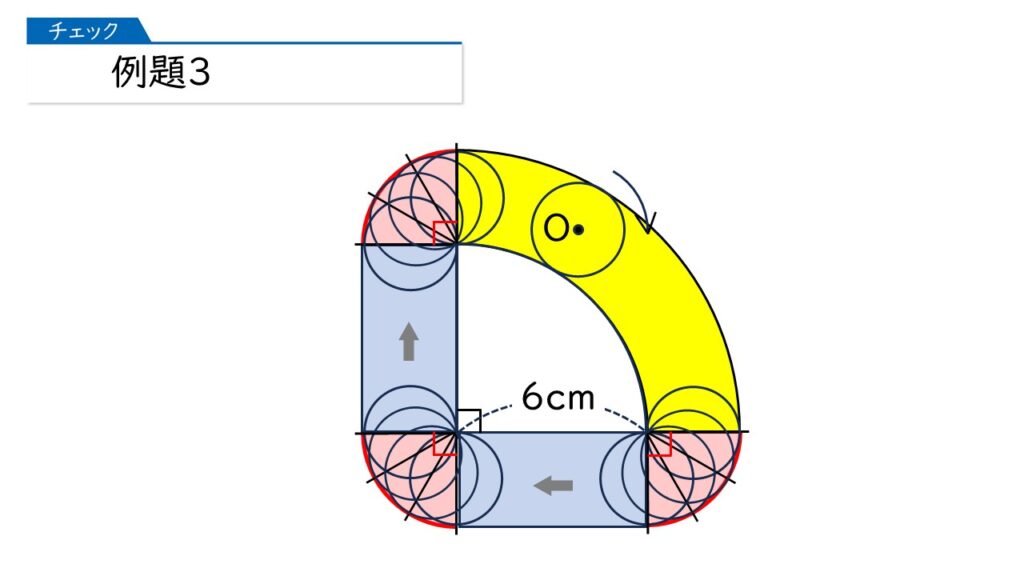
あっ、なるほど。黄色の部分は、大きいおうぎ形の面積から小さいおうぎ形の面積を引けばいいのね。すると、次のように求まるわ。
10×10×$\dfrac{1}{4}$×3.14－6×6×$\dfrac{1}{4}$×3.14＋4×4×$\dfrac{3}{4}$×3.14＋48
＝(25－9＋12)×3.14＋48
＝135.92（cm2）
大正解です、おめでとうございます！
予習シリーズ算数 円の回転・転がり移動 例題4
例題4（1）の解き方
例題4に進みましょう。まずは（1）です。
下の図のように、半径2cmの円が、折れ線にそって、アの位置からイの位置まで転がります。このとき、円の中心Oが動いたあとの線の長さは何cmですか。
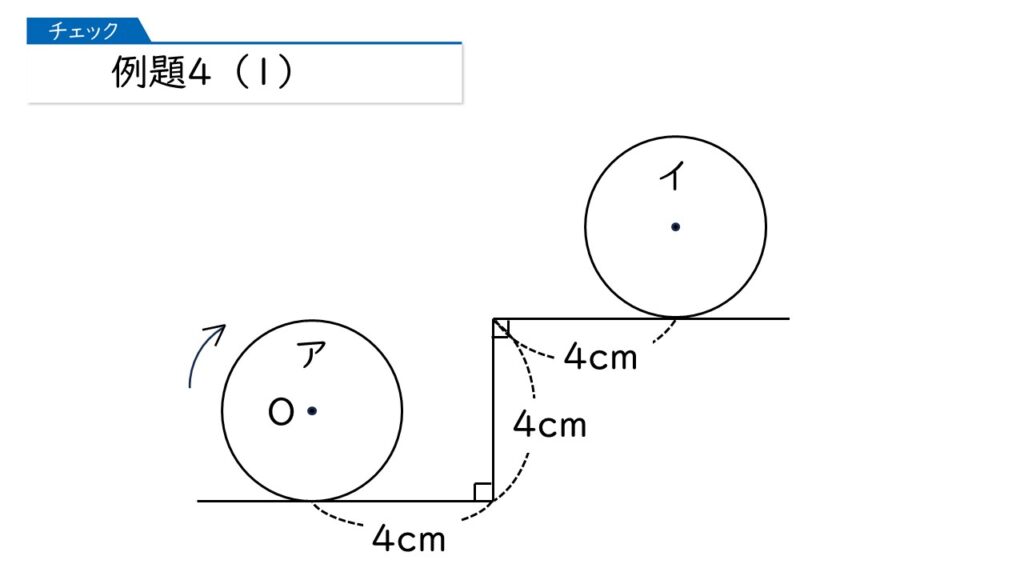
例題2や、例題3で使ったコツをここでも使いましょう。
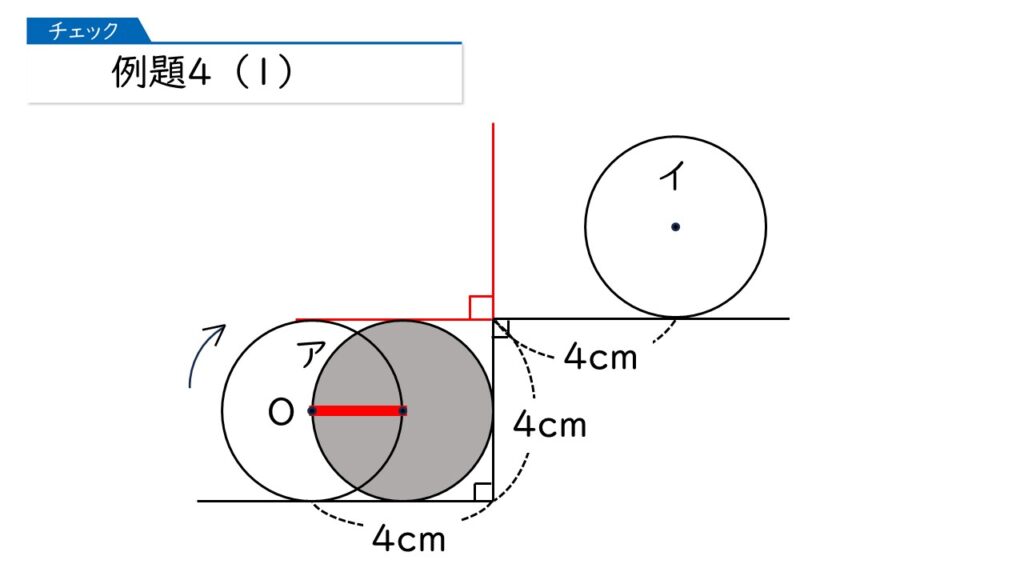
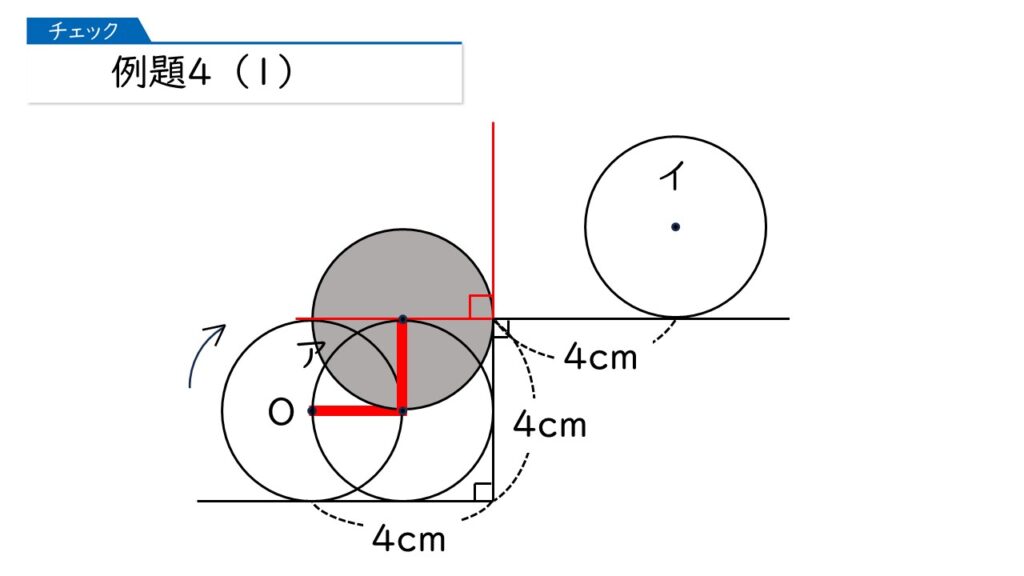
円が1周するあいだに、「転がるところ」と「円周上の1点を中心に回転するところ」があります。この2つの部分の境目に、下の図のような補助線を書きます。
このような補助線を引いたあと、円をどんどん転がしていきます。ここでは、中心Oが動くようすも同時に書いていきますよ（赤い線）。
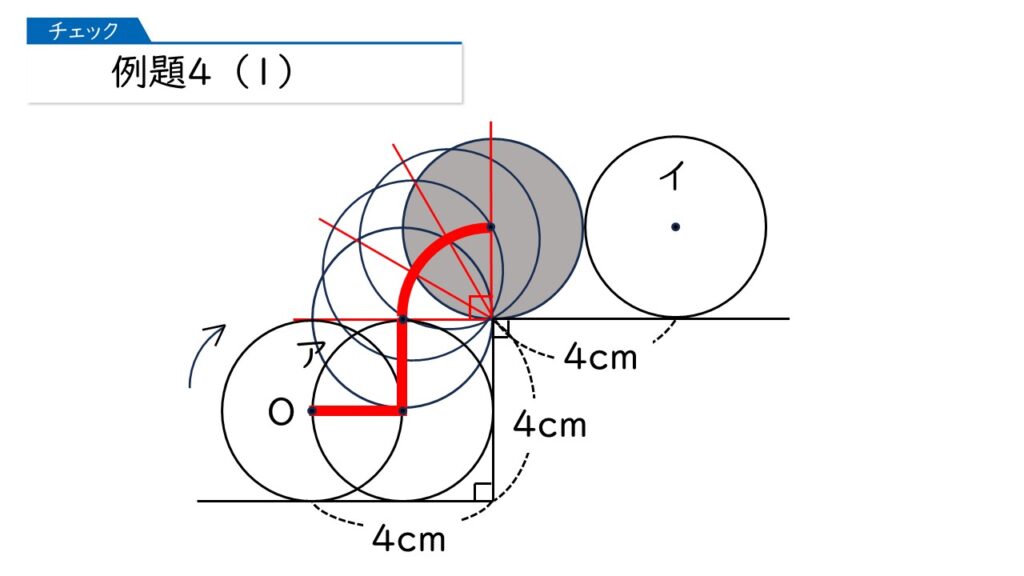
これはカンタンね。次のようにして答えが出るわ。
2＋2＋4×3.14×$\dfrac{1}{4}$＋4＝11.14（cm）
そうです、正解です！
例題4（2）の解き方
次に（2）です。円が動いたあとの図形の面積は何cm2になりますか？
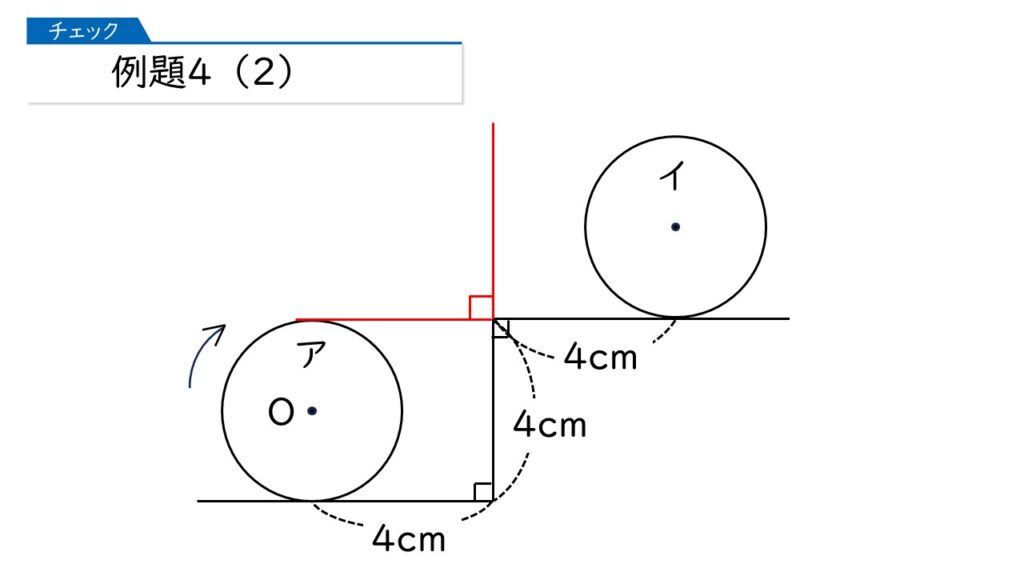
円をどんどん転がしていきますよ。
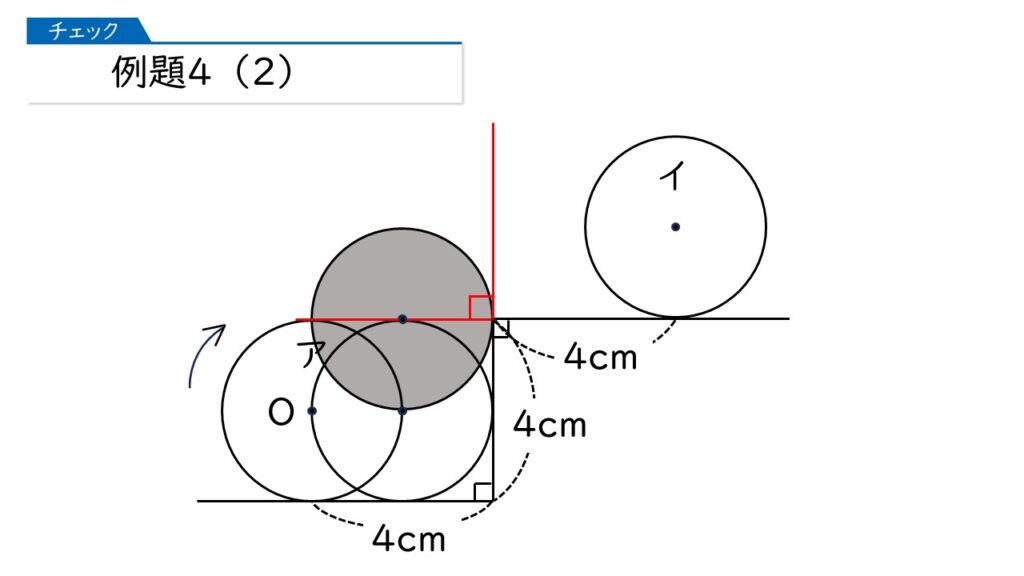
さあ、ここまでで、円が動いたあとの図形はどの部分になりますか？
下の図の黄色と青色の部分じゃないかしら。
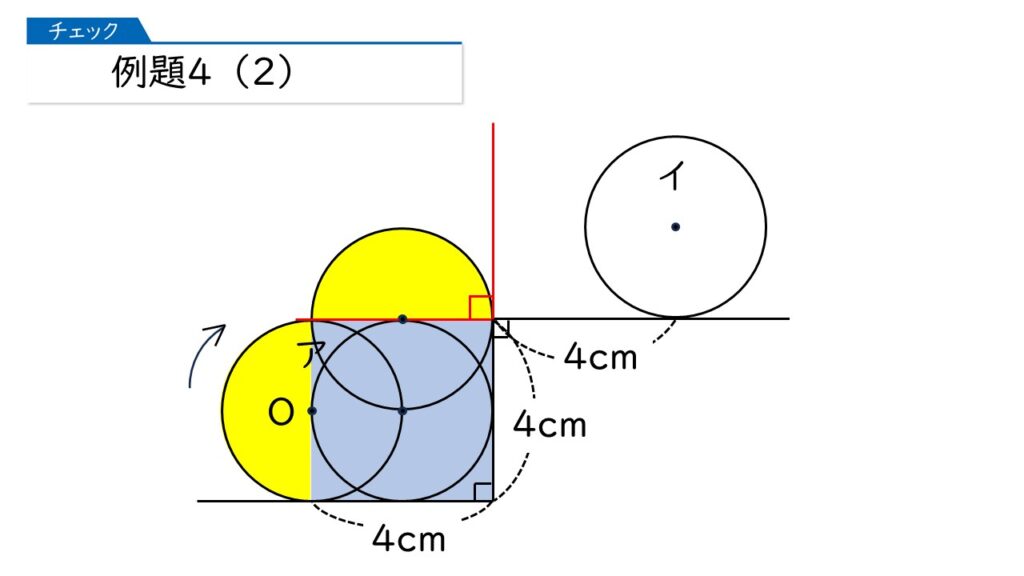
惜しいです。右下の赤色の部分は通っていないんです。
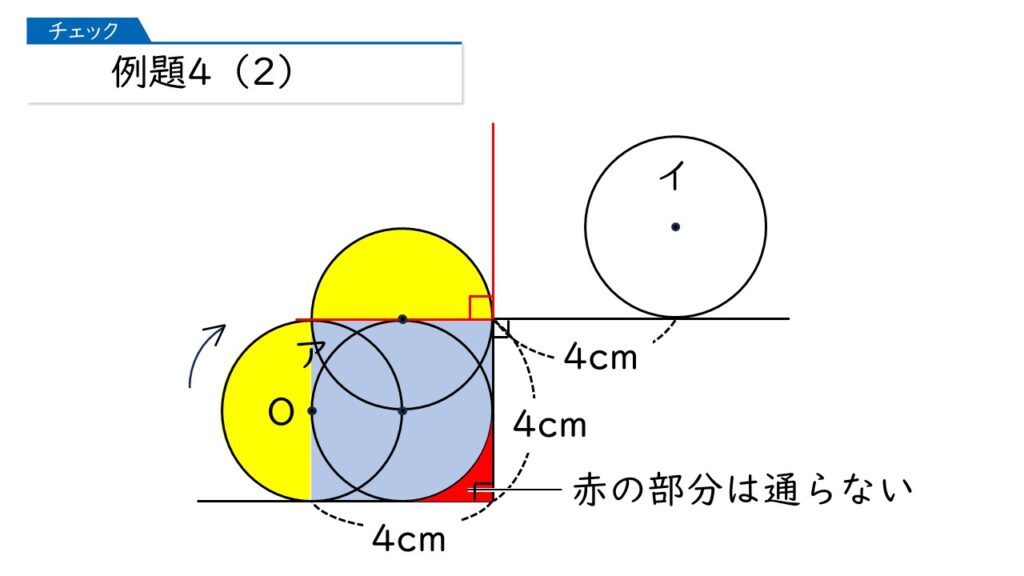
言われてみればそうだわ！
では、先に進めますね。
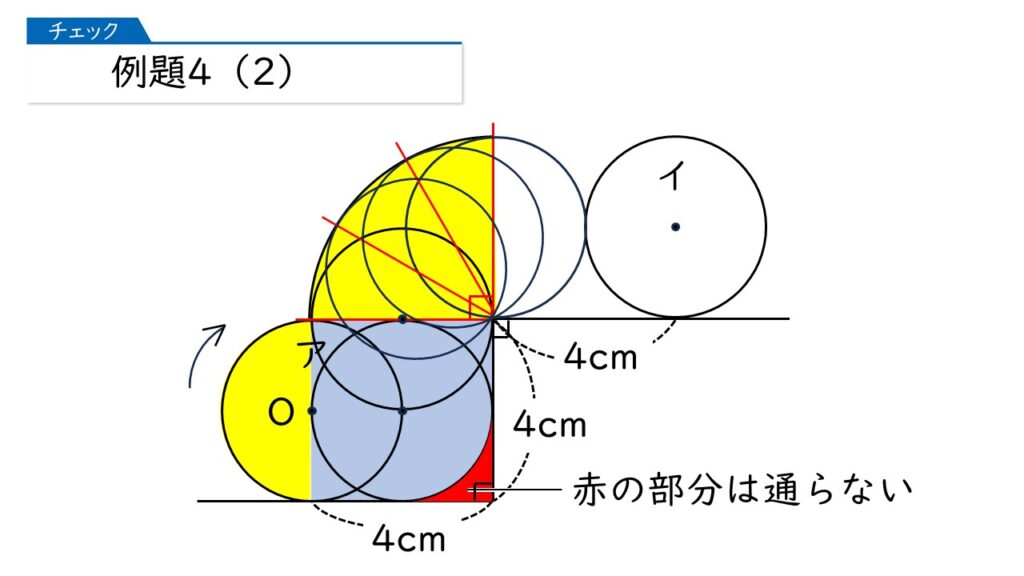
これで求められそうですね。
そうね。両はしの半円はくっつけて1つの円にできるわ。すると、下の式で答えを求めることができるわね。
2×2×3.14＋4×4×3.14×$\dfrac{1}{4}$＋32－(2×2－2×2×3.14×$\dfrac{1}{4}$)
＝57.12－0.86
＝56.26（cm2）
よくできました、さすがです！
予習シリーズ算数 円の回転・転がり移動 例題5
例題5の解き方
これで最後。例題5に進みましょう。
下の図のように、点A、Bをそれぞれ中心とする半径3cmの円が、くっついています。この2つの円のまわりにそって、点Oを中心とする半径3cmの円が転がりながら1周してもとの位置にもどります。このとき、点Oが動いたあとの線の長さは何cmですか。
この問題も、途中をしっかり書くことが大事ね。
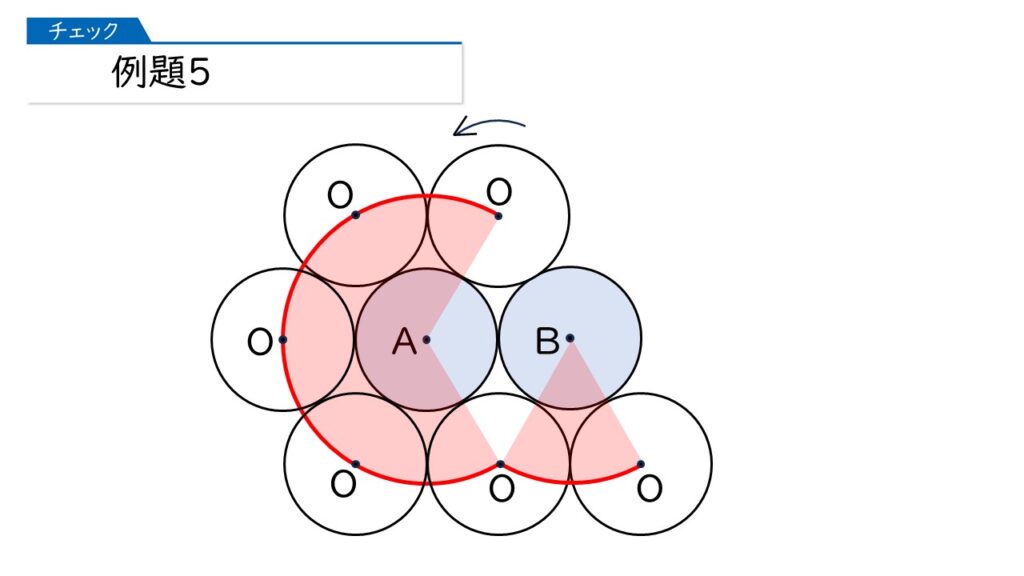
その通りです。さっそく、動かしてみましょう。点A、点Bを中心とする円の真ん中から動かし始めますね。
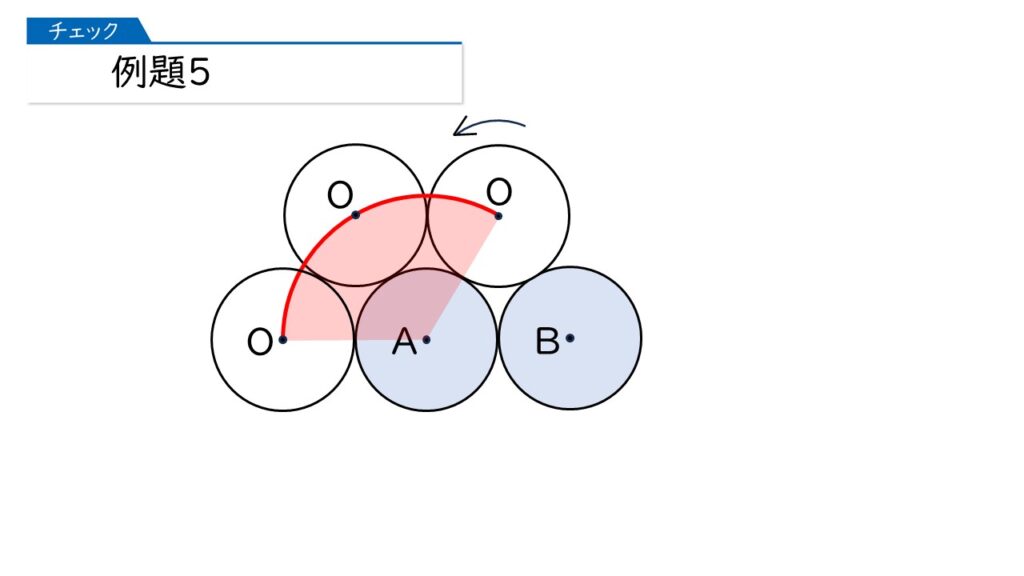
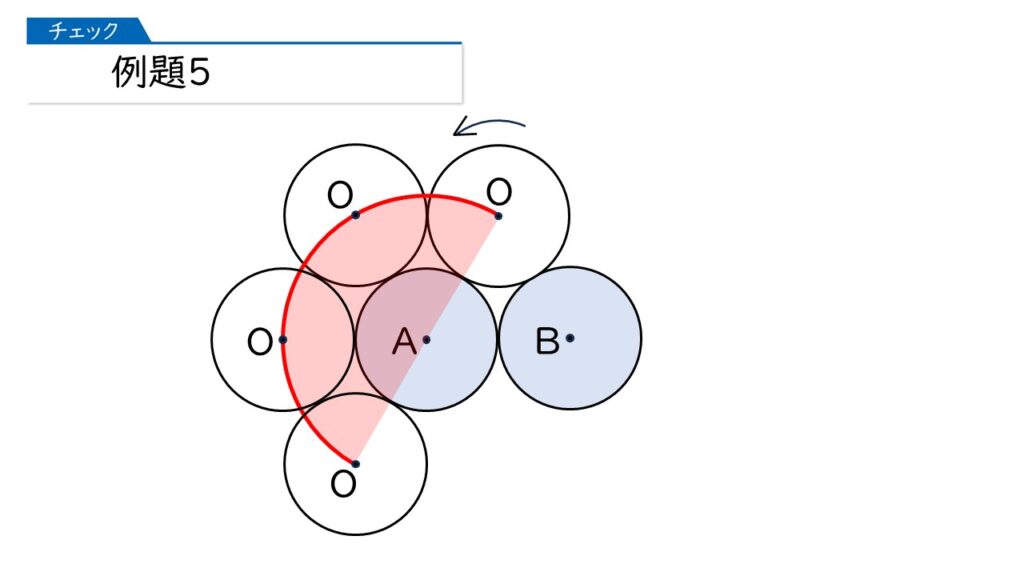
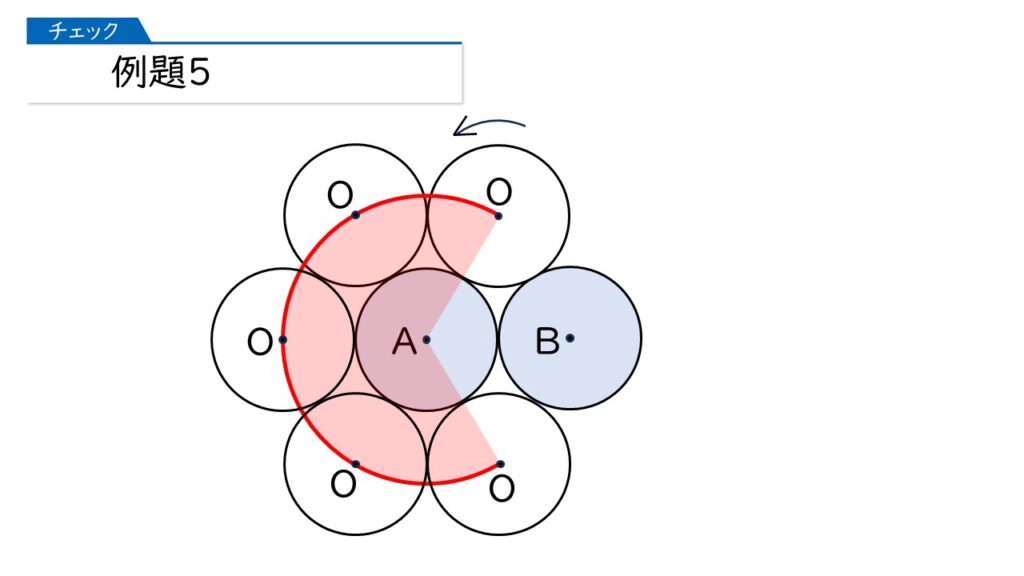
このあと、どのように動きますか？これまでは、点Aを中心にして動いていましたが、ここから変化します。
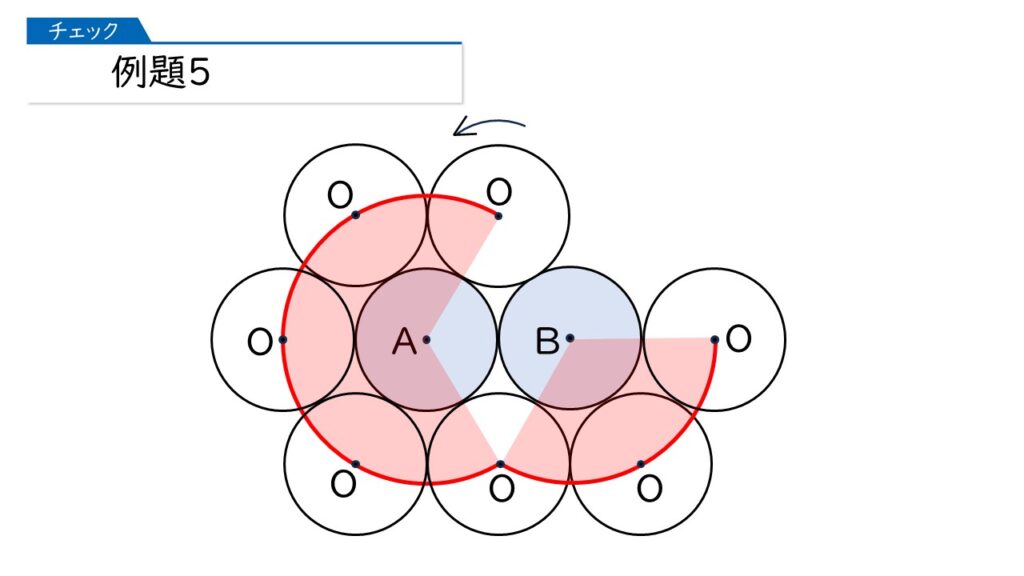
ここからは、点Bを中心にして動くのね！
すばらしいです、その通りです！ 勉強して慣れてくると、先を読めるようになりますね。
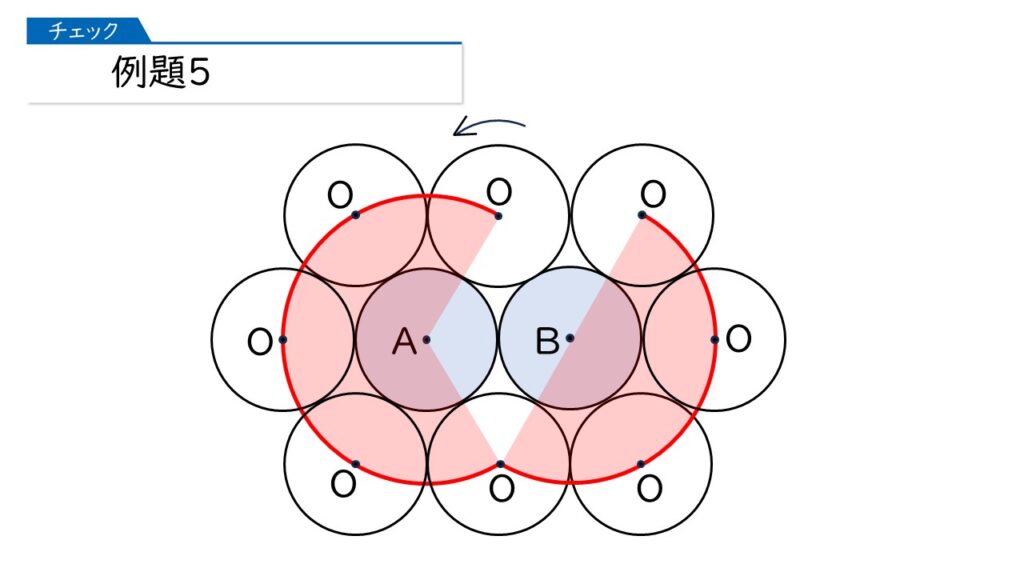
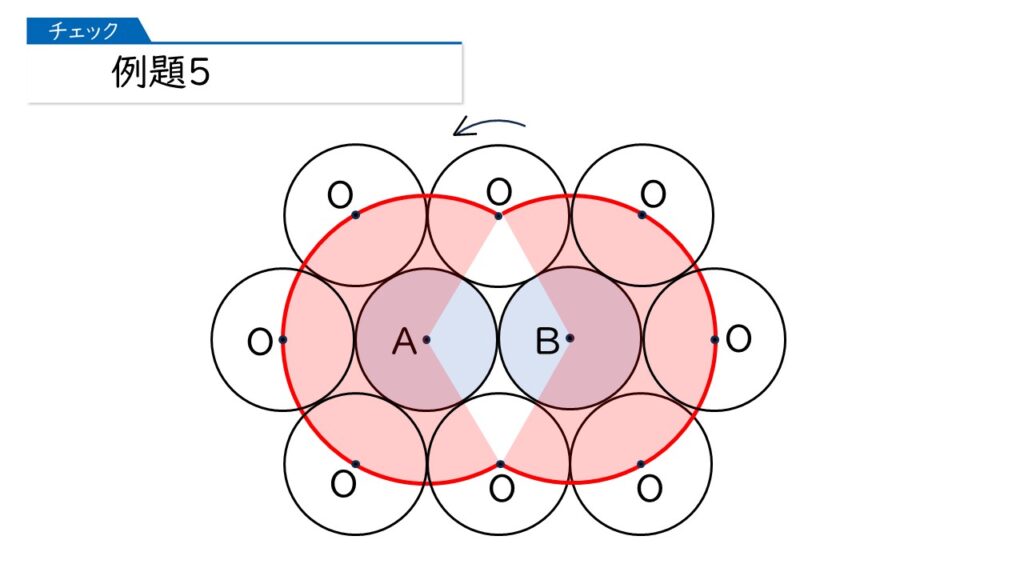
分かったわ！ 中心角240°のおうぎ形の弧の長さの2倍、ってことね。
だから、6×2×3.14×$\dfrac{240}{360}$×2＝50.24（cm）が正解ね。
その通りです！
途中の経過をしっかり書くと、自信をもって答えられるわ。
例題5は、実は別の観点で出題される
一つ注意なのは、例題5はこのまま入試で出題されることはありません。実際の入試では、「円Oが1周まわって元の位置にもどるまで、何回転しますか。」というふうに聞かれます。
えっ、何か難しそう…
慣れない人には難しいですけど、一度理解してしまえば簡単ですよ。下の動画で理解してくださいね。
分かった、やってみるわ。
予習シリーズ算数 小5前期 多角形・円の回転・転がり移動 まとめ動画
前回と今回で、図形の回転・転がり運動を見てきました。復習として、まとめ動画を用意しましたので、ぜひご覧ください。
スポンサーリンク
ABOUT ME
YouTube「クイックラーニング」、学習塾「アカデミーワン」をやっています。中学受験で疑問や不安を抱えている方に、中学受験の本質にさかのぼって、ゆるぎない受験対策ができるようにお手伝いしています。
【著書】「中学受験は親で決まる」（2008年）「優秀な子どもが中学受験で失敗する9の理由」（2010年）
【AERA Kids取材】「9歳10歳の危機」（1012年夏号）、「学力の差は夏で決まる」（2013年秋号）
【著書】「中学受験は親で決まる」（2008年）「優秀な子どもが中学受験で失敗する9の理由」（2010年）
【AERA Kids取材】「9歳10歳の危機」（1012年夏号）、「学力の差は夏で決まる」（2013年秋号）
