四谷大塚 予習シリーズ 算数 徹底解説 5年上第2回 いろいろな図形の面積-クイックラーニング
第2回.jpg)
今回は、予習シリーズ算数の小5前期、「いろいろな図形の面積」を見ていきますね。

図形は難しそうでイヤだわ…

少しずつ、段階をふんでいけば大丈夫ですよ! まずは、面積の公式から確認しましょう!



予習シリーズ算数 図形の面積の復習
長方形の面積の求め方
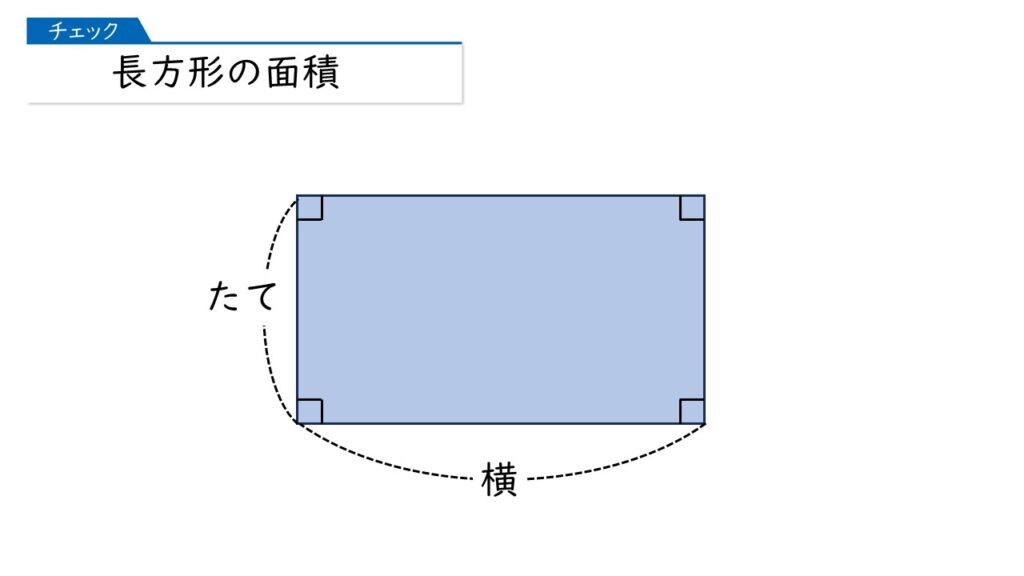
長方形の面積は「たて×横」ですね!

それくらいわかるわ!

ですね。では、平行四辺形の面積はどのように求めますか?

平行四辺形の面積の求め方
長方形の一部分である直角三角形(斜線部分)を左に動かしますね。

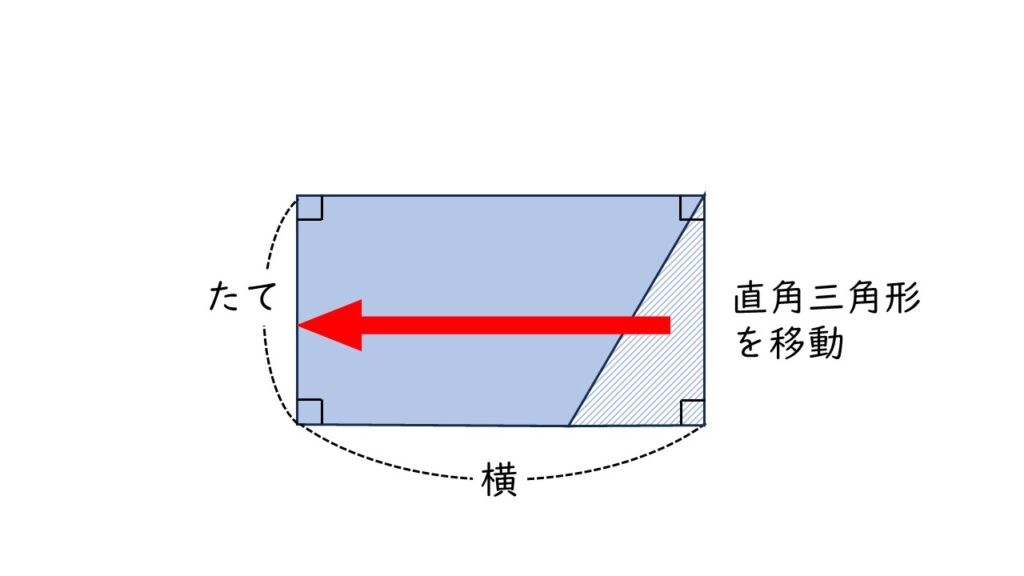
そうすると、平行四辺形ができます。さて、この平行四辺形の面積はどのように求めますか?


長方形と同じになるのね。平行四辺形の面積は「底辺×高さ」で求まるわ!

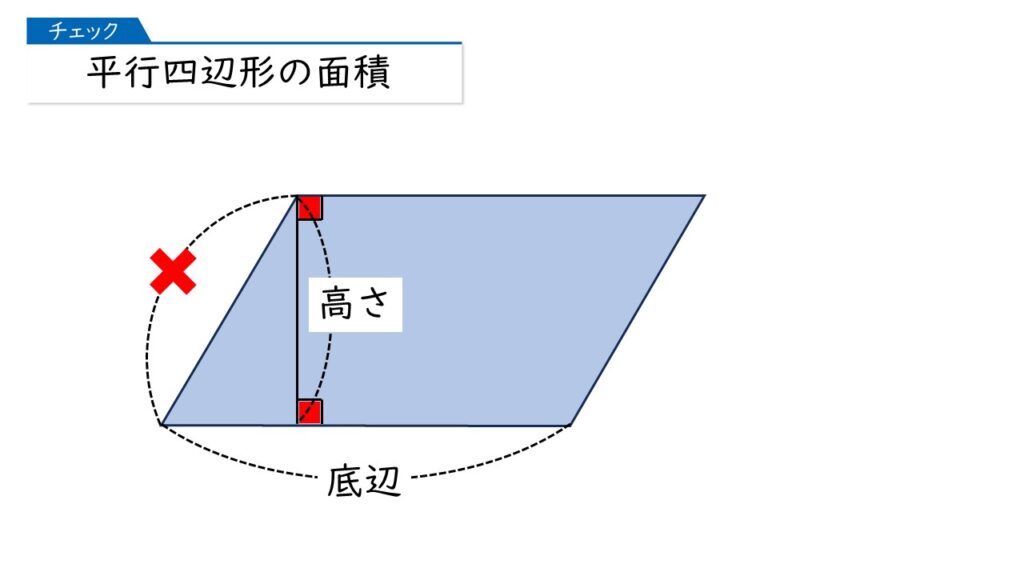
その通りです! くれぐれも、「赤の×」(直角三角形の斜辺)の部分を「高さ」にしないことが大事ですね。「赤の×」のところは、底辺と直角になっていませんから。

台形の面積の求め方
次に、台形の面積はどのように求めることができますか?
ポイントは、元の台形をコピーして、180°回転させて、元の台形につないでみることです。

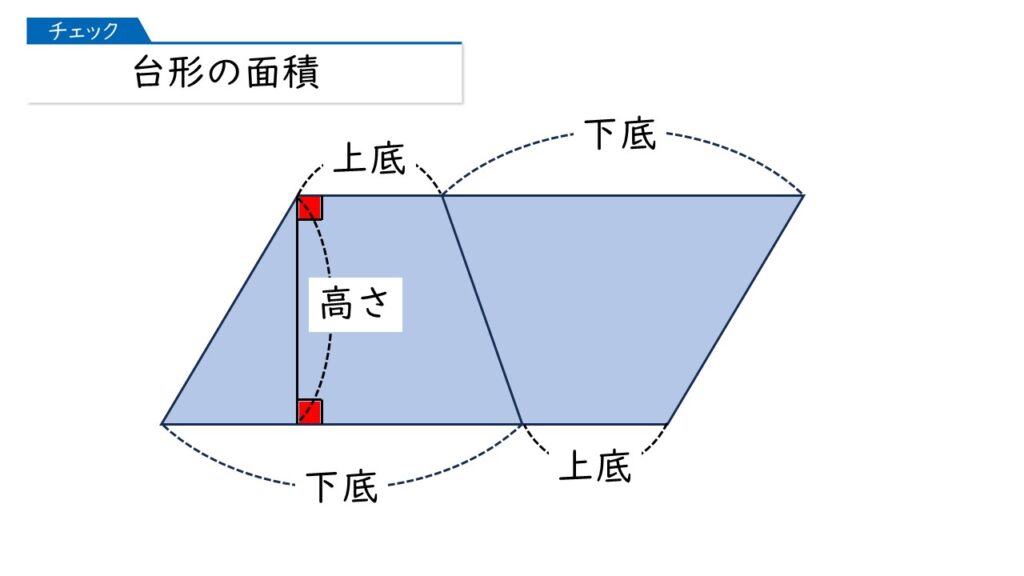
平行四辺形になるわ!つまり、平行四辺形の面積の出し方を利用すればいいのね。

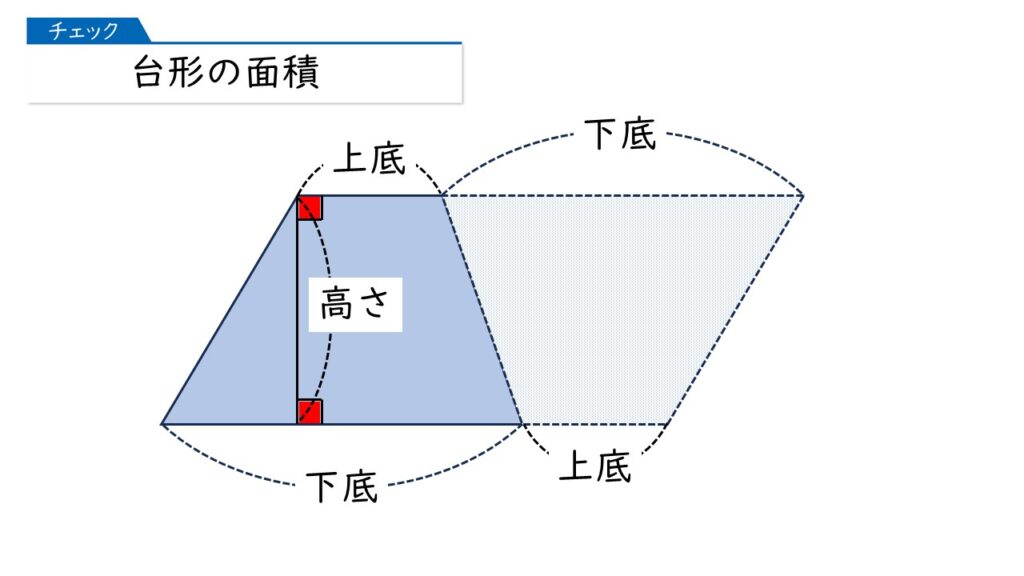
そうですね!台形の面積は次のように求まります。
(上底+下底)×高さ×$\dfrac{1}{2}$
次にひし形の面積をみていきましょう。

ひし形の面積の求め方
まず、ひし形の2本の対角線が直角に交わっていることに注意しましょう。これを使えば、ひし形の面積を求めることができます。


つまり、ひし形の面積は「対角線×対角線」ってこと?

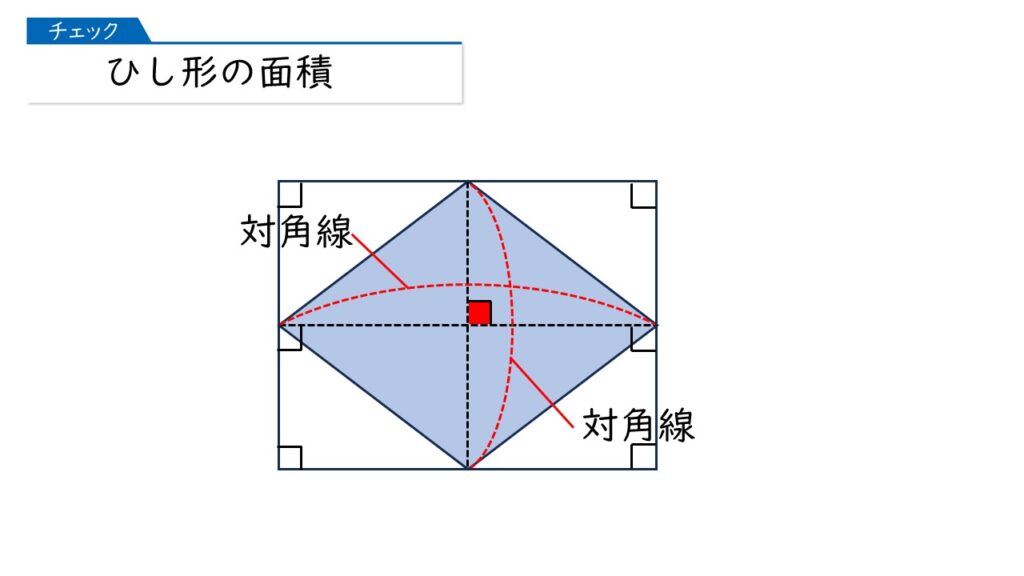
おしいです!「対角線×対角線」をすると、もとのひし形の面積の2倍になってしまいます。

なるほど。そうすると、ひし形の面積は「対角線×対角線×$\dfrac{1}{2}$」ですね。

すばらしいです!
では面積の確認はここまでにして、次は例題に進みましょう。

予習シリーズ算数 図形の面積 例題1
予習シリーズ算数 図形の面積 例題1(1)
下の図で、ぬられている図形の面積を求めます。この図形は何ですか?


台形!

その通りです! そうると、面積は…

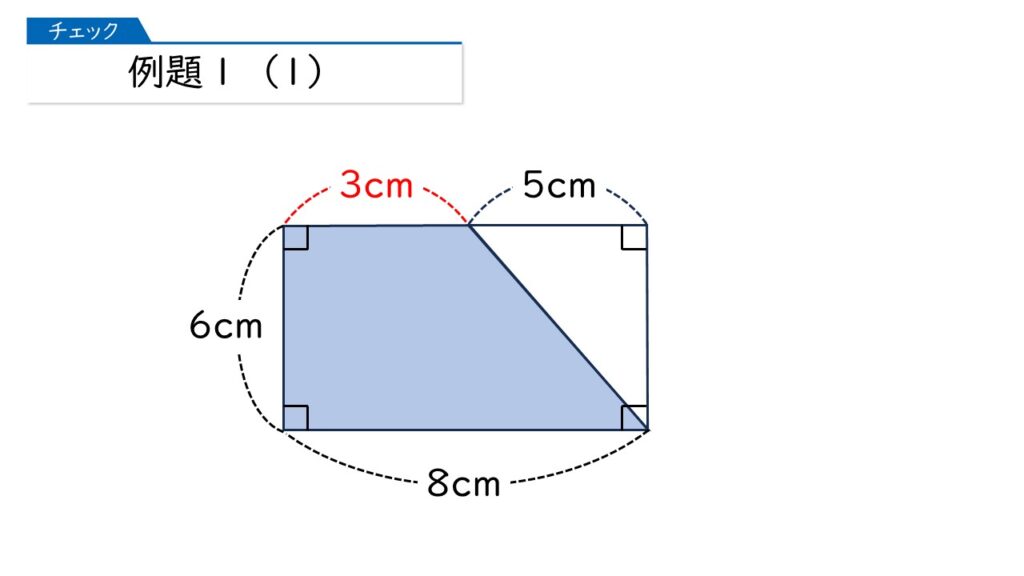

そうです!では(2)を見てみましょう。ここでも、ぬられた図形の面積を求めます。

予習シリーズ算数 図形の面積 例題1(2)
下の図で、ぬられている図形の面積を求めます。この図形はどのようにすれば求まりますか?


この四角形は、どの公式にもあてはまりそうにないんですけど、2つの直角(赤の部分)に注目して、2つの三角形に分けて求めることができます。

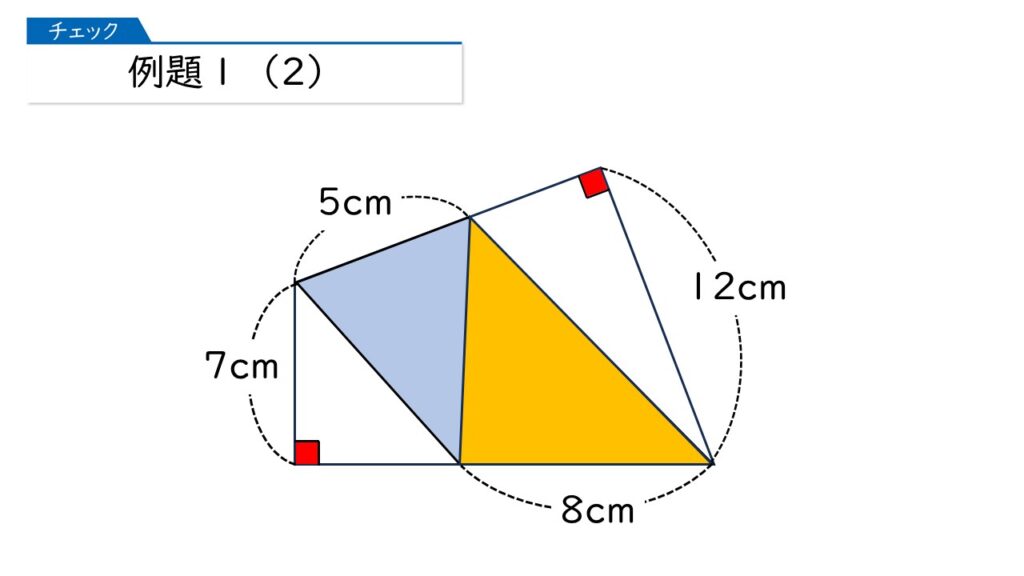
このように、青と黄色の三角形に分けました。それぞれの面積を求めることはできますか?


青の三角形では、底辺の長さが分かってるけど、高さが分かっていないわ。

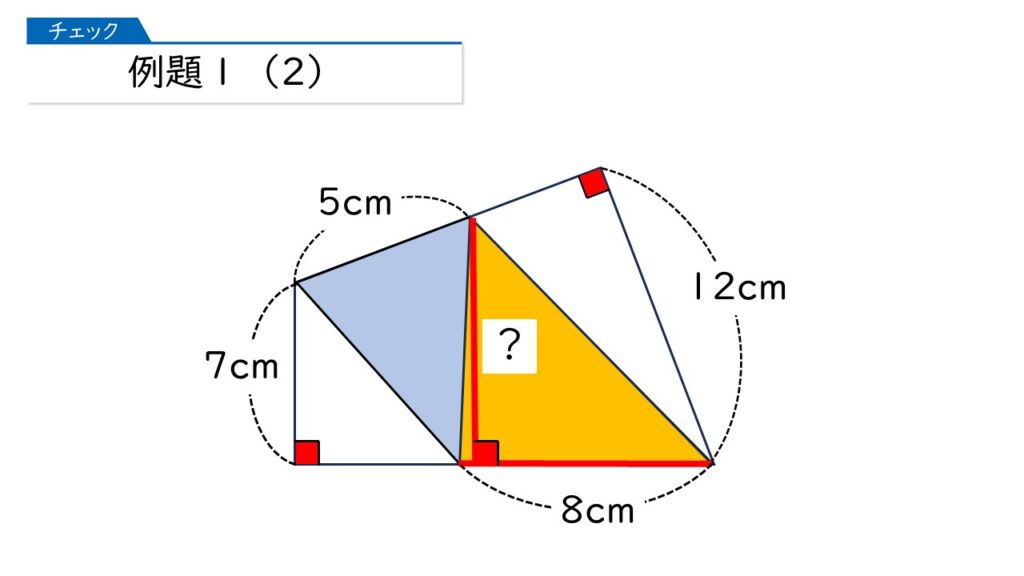
黄色の三角形も、底辺の長さが分かってるけど、高さが分かっていないわ。

そうですね。じゃぁ、下の図のように2つに分けたらどうでしょう?

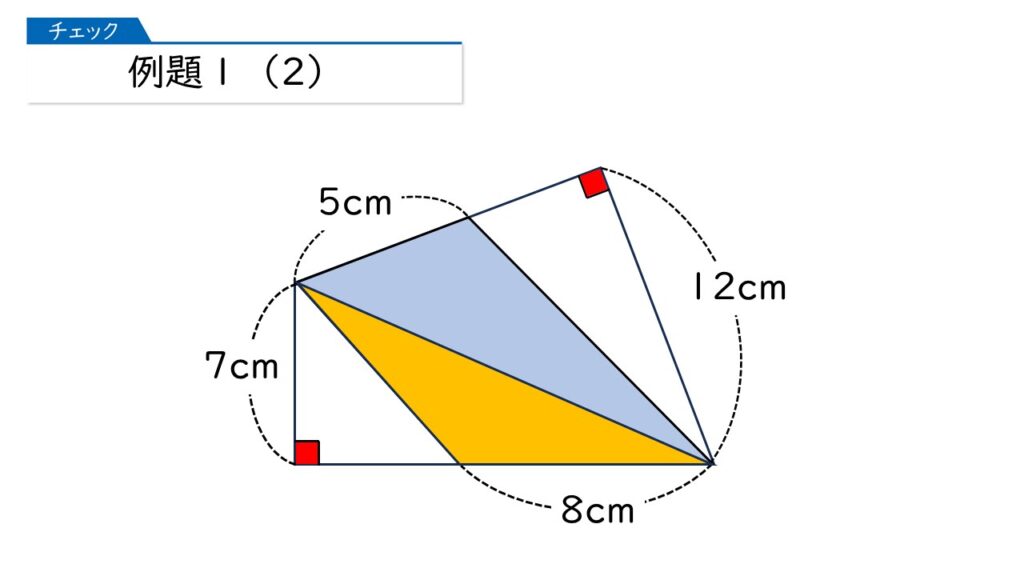
なるほど、黄色の三角形も、青の三角形も、底辺と高さの長さが分かるのね!

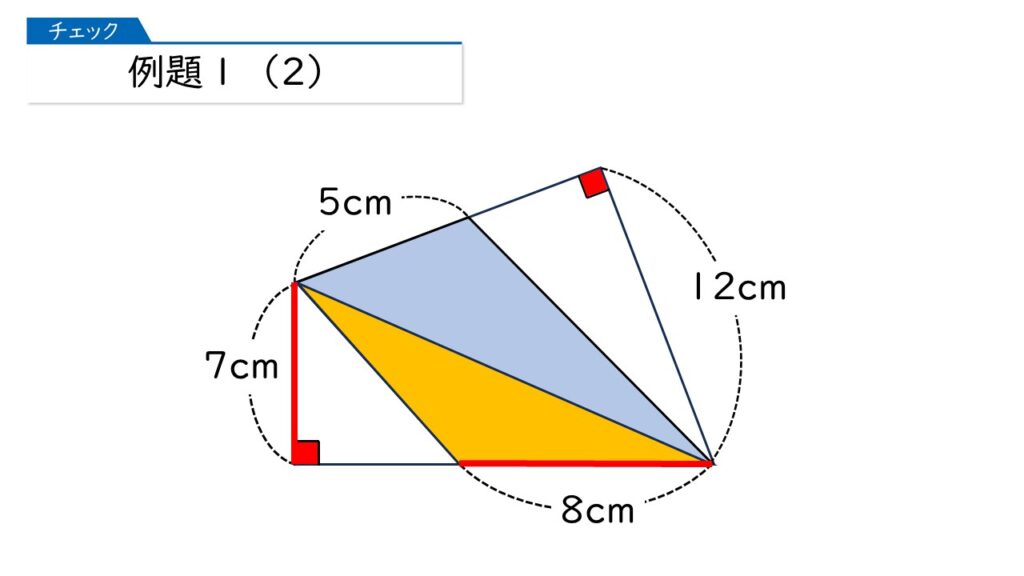
そうです! 底辺と高さは垂直の関係にあるってことが重要ですね。
黄色の三角形の面積は、8×7×$\dfrac{1}{2}$=28(cm2)です。

したがって、正解は、28+30=58(cm2)。

できました! それでは、例題2に進みましょう! 円がからんだ図形のぬられた部分の面積を求めます。

予習シリーズ算数 図形の面積 例題2
おうぎ形の面積の復習
おうぎ形の面積はどのようにして求めますか?


おうぎ形は円の一部だから、円の面積の求め方を利用すればいいのね。

そうです。半径×半径×3.14×$\dfrac{中心角}{360}$ で求めることができます。

予習シリーズ算数 図形の面積 例題2(1)
例題2(1)は、おうぎ形の中に直線を1本引いた図で、中の三角形は正三角形です。ぬられた部分の面積を求めましょう。

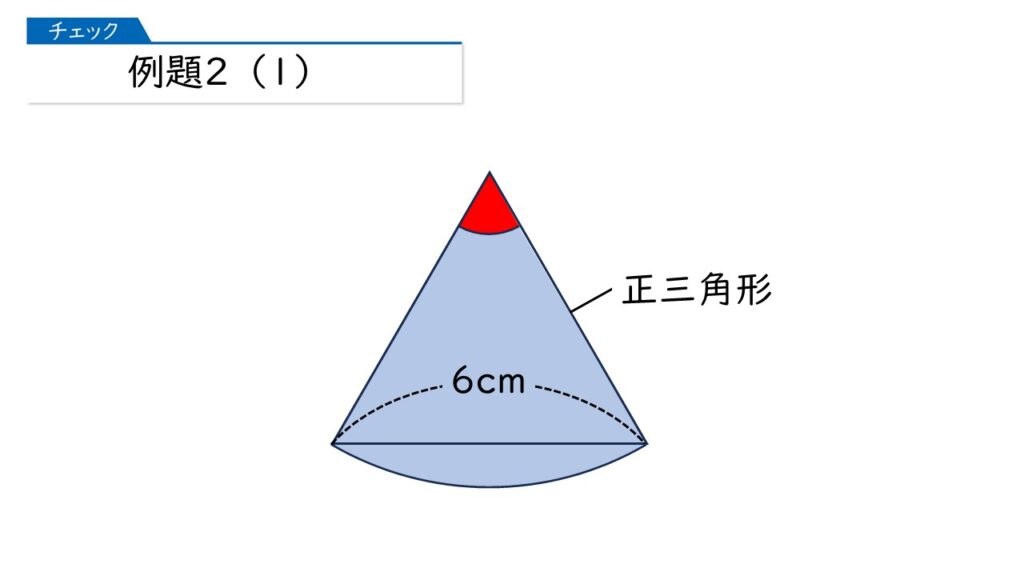
中心角の大きさと、半径の長さは分かりますか?


中の三角形が「正三角形」だから、半径も中心角も分かるわね。

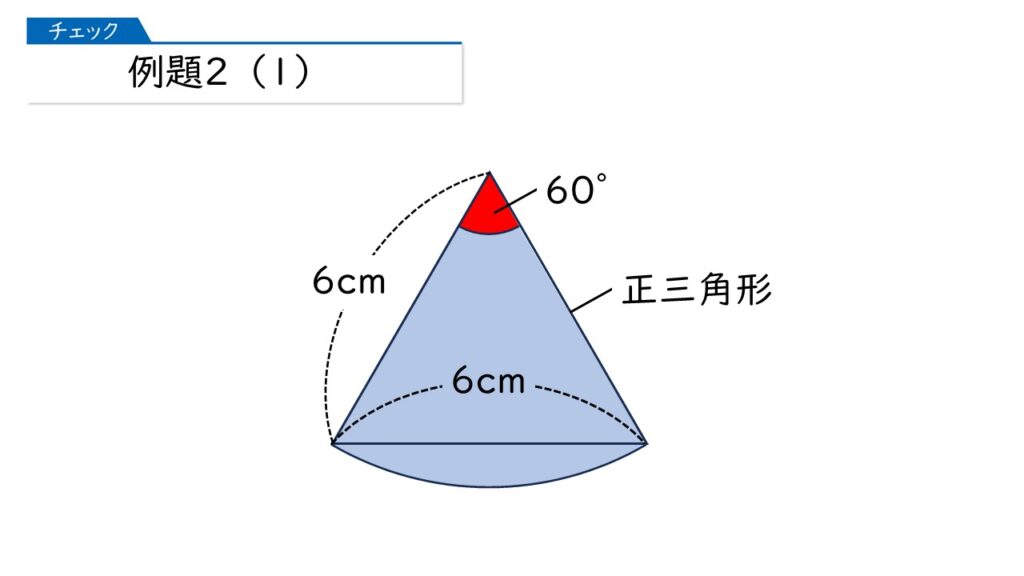
そうすると、ぬられた部分の面積は、おうぎ形面積だから、6×6×3.14×$\dfrac{60}{360}$ を計算すればいいわね。


予習シリーズ算数 図形の面積 例題2(2)
例題2(2)は、正方形と半円を組み合わせた図形の中に直線を1本引いたものです。点Mが半円の弧の真ん中であるとき、ぬられた面積を求めます。

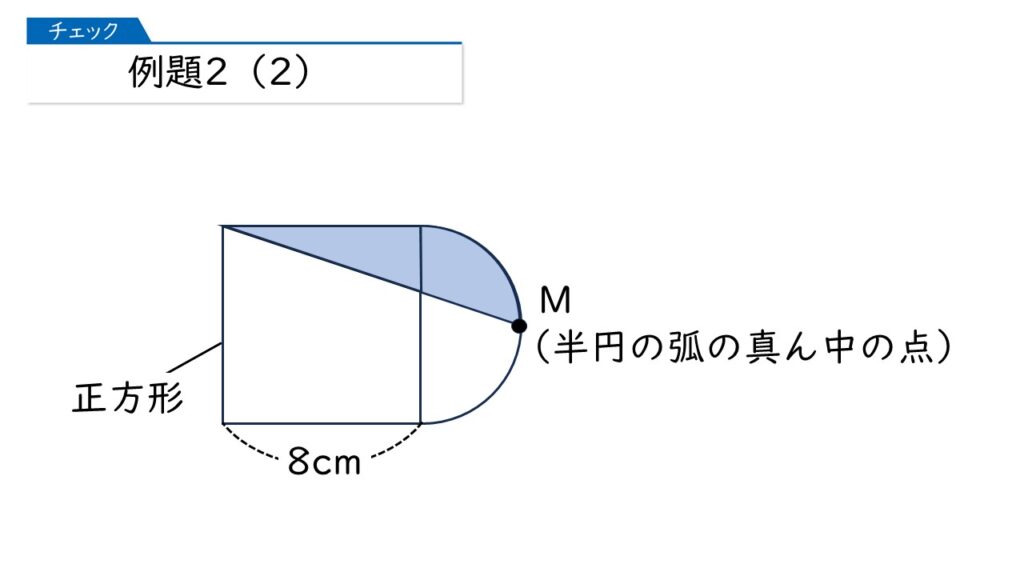
やっぱり出てきたわ。こんな形の図形の面積なんて出せるのかしら?

確かに難しいですね。ヒントを出しますね。

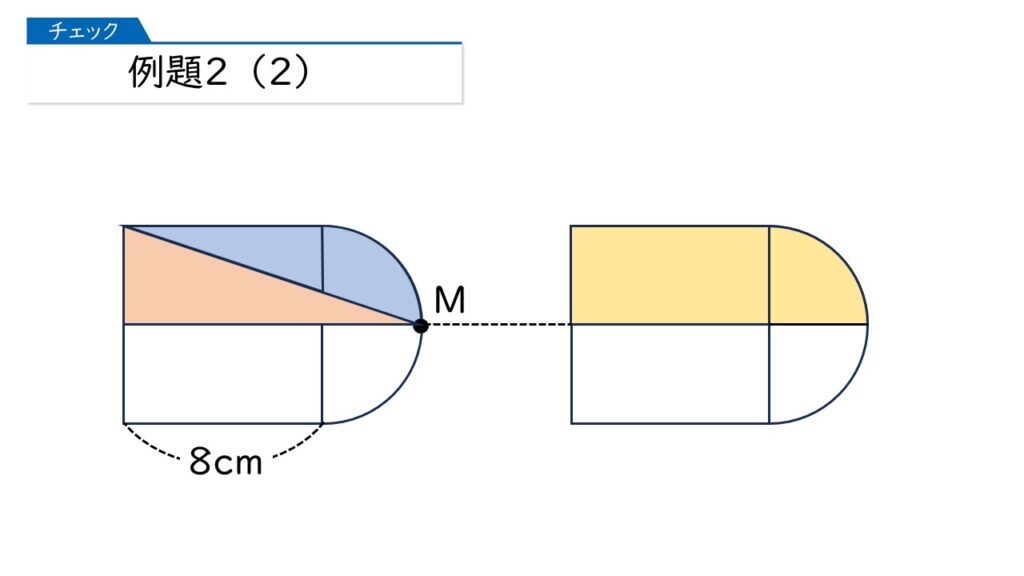
あっ、黄色の部分の面積から、赤の部分の面積を引けばいいのね!

その通りです!


もうできるわ。
Aの部分の面積は、4×8=32(cm2)。Bの部分の面積は、4×4×3.14×$\dfrac{90}{360}$=12.56(cm2)。 Cの部分の面積は、12×4×$\dfrac{1}{2}$=24(cm2)。 求める面積はA+B-Cだから、32+12.56-24=20.56(cm2)が答えね。

正解です、おつかれさまでした!

予習シリーズ算数 図形の面積 例題3
さあ、次は例題3です。下の図は、長方形の中に三角形をかいたものです。色のついた部分の面積を求めましょう。

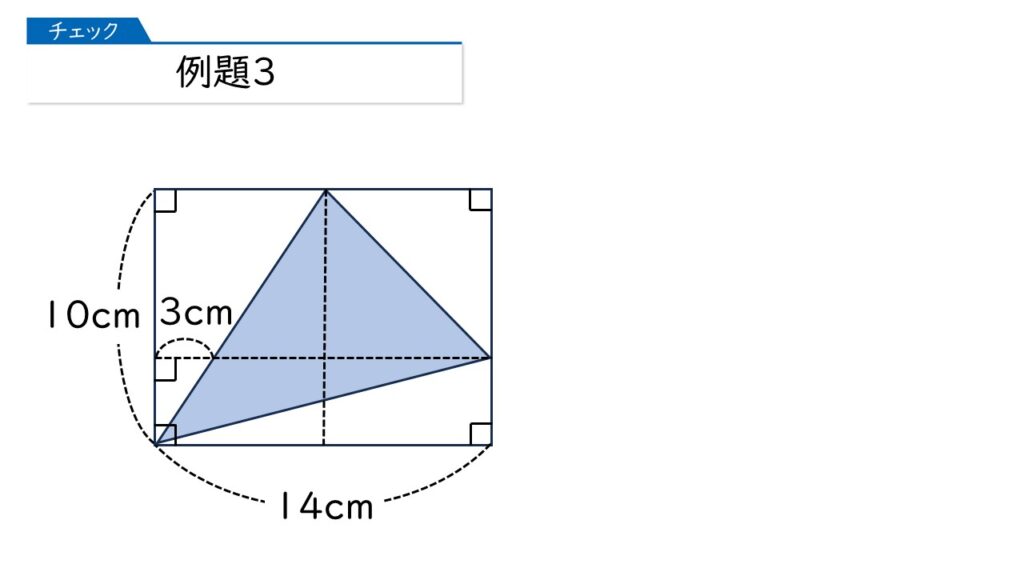
ん~、どうやって求めるのかしら…

上半分の三角形と、下半分の三角形に分けるといいですよ。

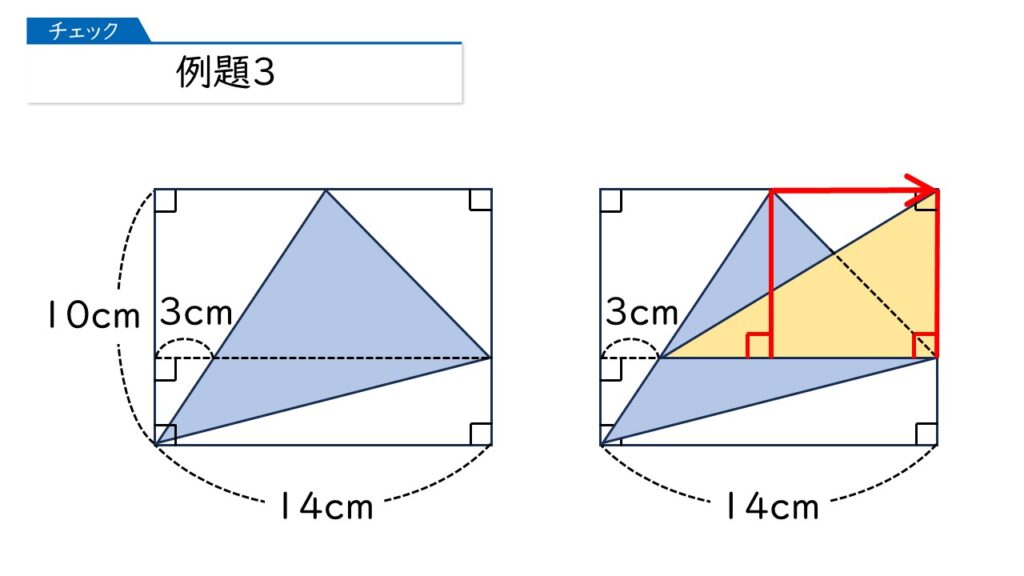
上半分の三角形の面積は、黄色の直角三角形の面積と同じになります。なぜかというと、底辺と高さの長さが同じになるからです。

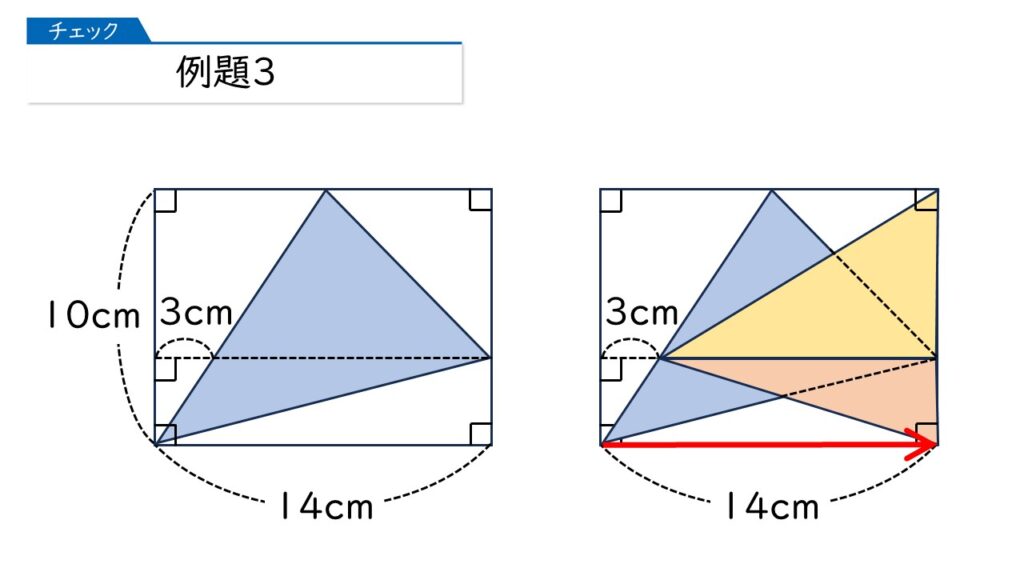
同じようにして、下半分の三角形の面積は赤の直角三角形の面積と同じになります。
このように、面積を変えずに三角形の形を変えることを「等積変形」といいます。

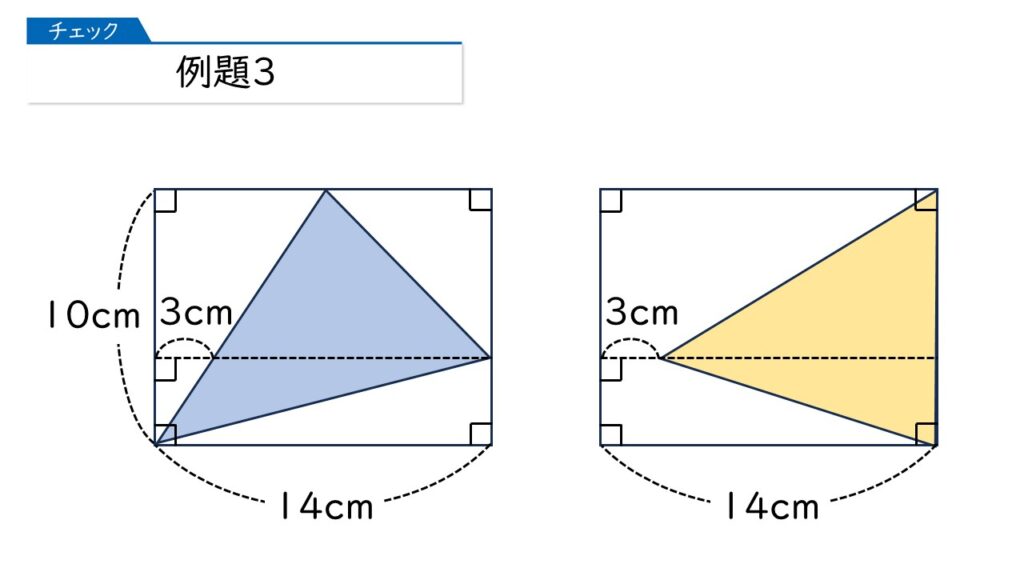
そうすると、求める図形の面積は、上の右の黄色い三角形の面積と同じになるんですね。
だから答えは、10×(14-3)×$\dfrac{1}{2}$=55(cm2)になります。もう一つ、別の方法でやってみましょう。


問題に、たての点線を入れました。これを利用することでも解くことができます。

やはり「等積変形」を使うのね。

そうです。下の図を見てください。

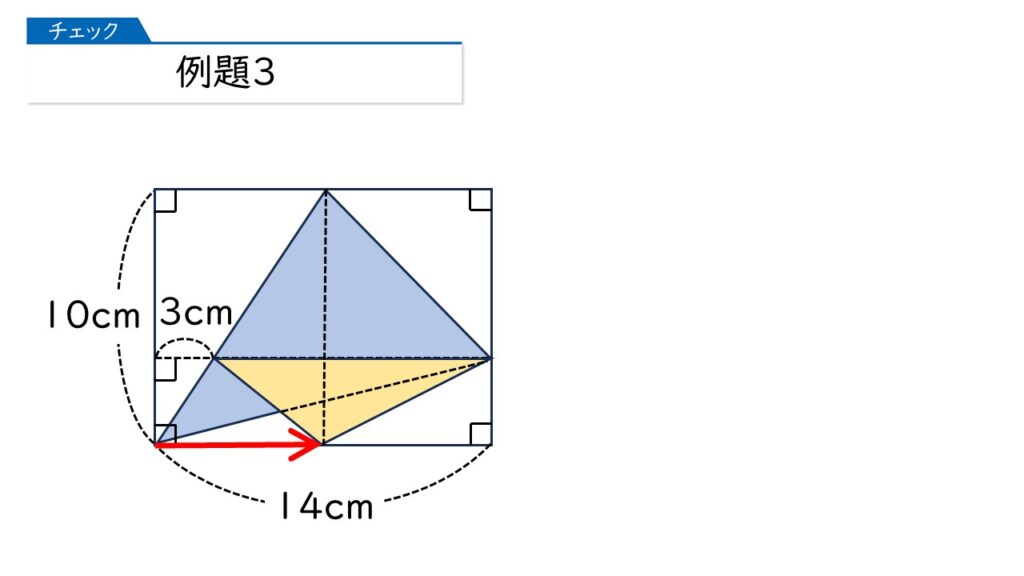
下半分だけ等積変形します。そうすると…


なるほど、右の黄色い図形の面積を求めればいいのね!
この黄色い図形の面積は、「ひし形の面積=対角線×対角線×$\dfrac{1}{2}$」を使って求めることができるわ。つまり、10×11×$\dfrac{1}{2}$=55(cm2)になるのね。

ご名答です!
算数の勉強で大事なことですが、カンタンな問題を何回も解いても、算数の実力は上がりません。
算数の問題を解くときは、ぜひ、いろいろな解き方を考えて欲しいんです。そうすることによって、いろいろな見方が身につくんですね。
算数の力を伸ばす勉強法は「5回解くより、5通りで解け」です!

予習シリーズ算数 図形の面積 例題4
予習シリーズ算数 図形の面積 例題4(1)
例題4(1)です。下の図は、対角線の長さが20cmの正方形です。この正方形の面積を求めましょう。

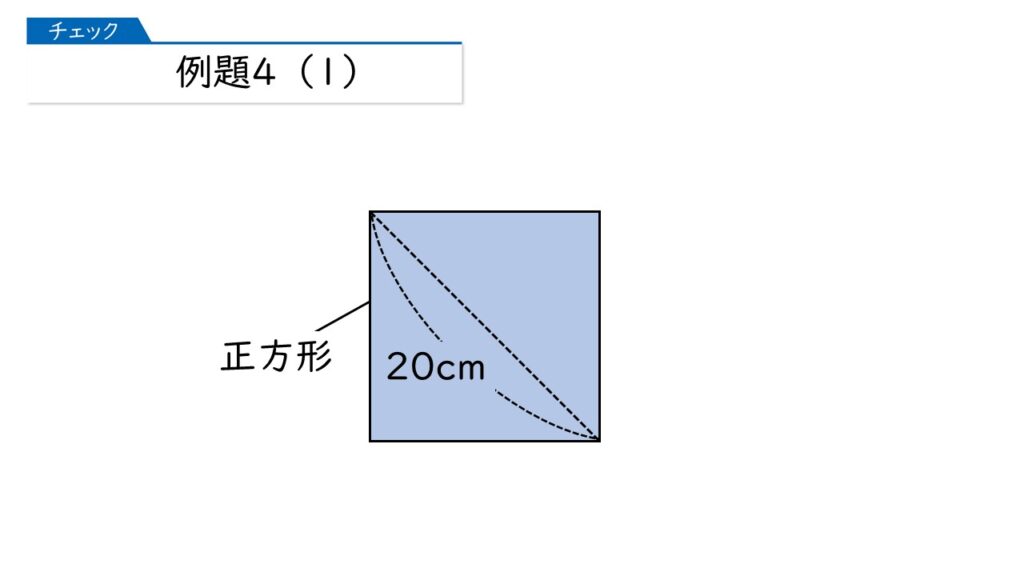
えっ、この図から正方形の1辺の長さが分かるんですか?

いい質問ですね~。実は、この正方形の1辺の長さは、中学生でやる平方根を使わないと表すことができません。
ですが、見方を変えると、面積は求めることができるんです。

へぇ~、どうやって求めるんですか?

下の図のように、外側に大きな正方形を書くとどうですか?

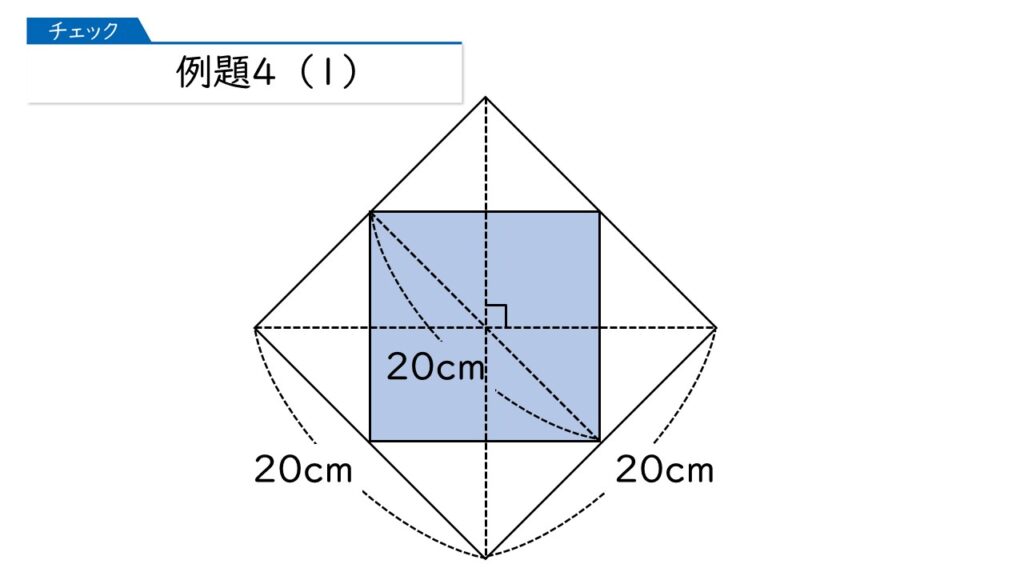
あっ、なるほど。外側の大きな正方形の面積を求めることができるから、その面積を半分にすればいいのね!


予習シリーズ算数 図形の面積 例題4(2)
では、例題4(1)を使って、例題4(2)を解いてみましょう。
下の図は、(1)の正方形の中に四分円を書いたものです。ぬられた部分の面積を求めましょう。

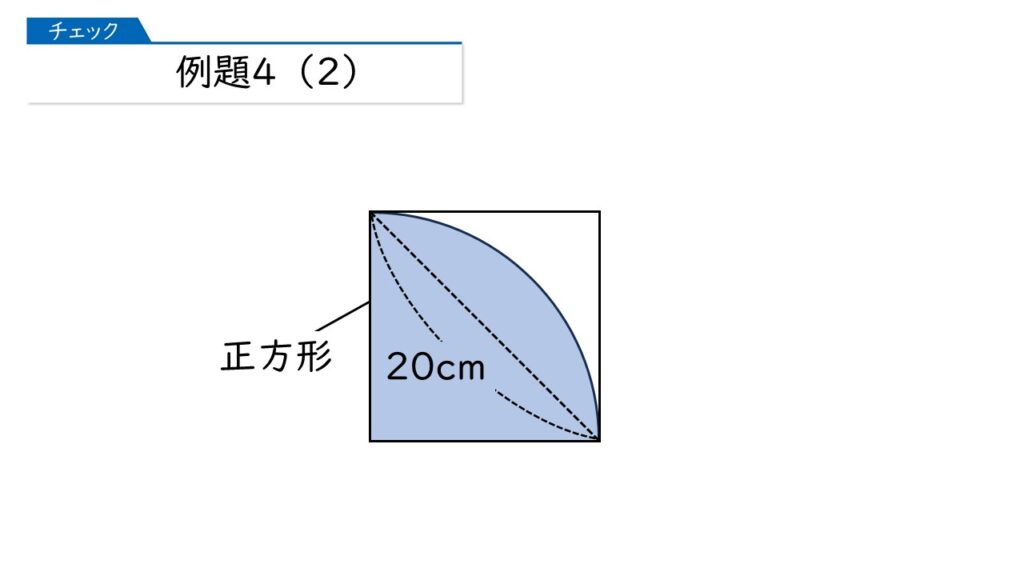
おうぎ形の面積なんだけど、中心角は90°だけど、半径が分からないから、面積を求めることができない…

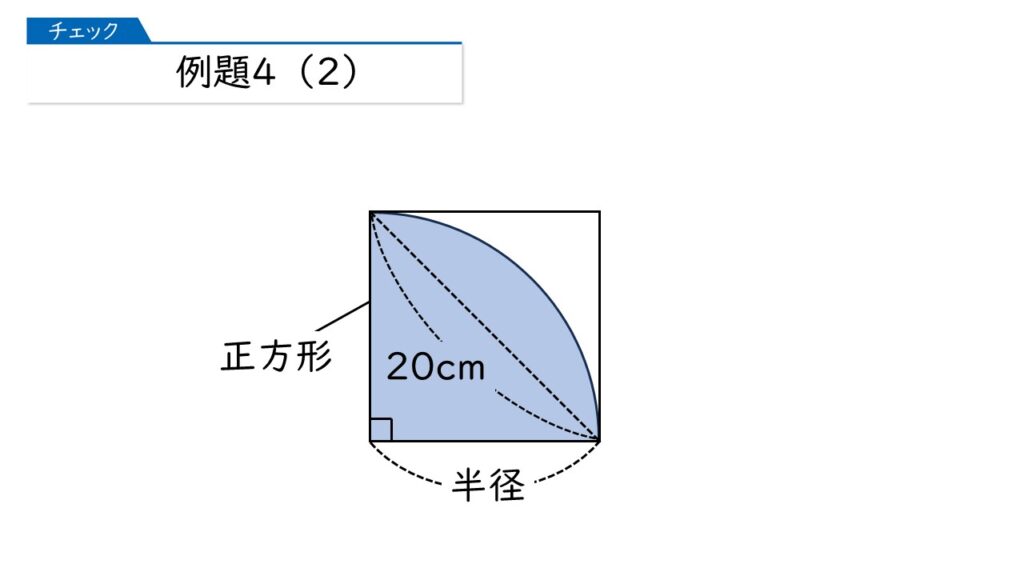
おうぎ形の面積を求める公式は何でしたっけ?

半径×半径×3.14×$\dfrac{中心角}{360}$ ですね。

ですね。ならば、半径の長さが分からなくても、「半径×半径」の値が分かっていれば、面積を求めることができますよ。

そうか! このおうぎ形の「半径×半径」の値は、正方形の面積と同じね。
正方形の面積は「対角線×対角線×$\dfrac{1}{2}$」で求めることができるから、このおうぎ形の「半径×半径」の値は「20×20×$\dfrac{1}{2}$」よね。

できましたね!
答えは、20×20×$\dfrac{1}{2}$×3.14×$\dfrac{90}{360}$=157(cm2)になります。
予習シリーズ算数 図形の面積 例題5
三角形の合同
【例題5】に入る前に、ここでのテーマである「三角形の合同」についてみておきましょう。

「合同」は「形も大きさも同じ図形」ということね!

そうです! 三角形の合同条件は、3つありますよ。


三角形の合同条件は、解説動画と練習問題がありますので、下の動画で学習してください。
三角形の合同条件は、少し説明したくらいでは小学生の頭には残りませんので、ぜひ、保護者の方と一緒に動画を見てください。

予習シリーズ算数 図形の面積 例題5(1)
では、例題5(1)をみてみましょう。下の図は、正三角形ABCの中に直線を2本引いたもので、BDとCEの長さが等しくなっています。


「正三角形」と「BD=CE」というのがポイントですね。分かっていることは、図に書き足しましょう。


このときに、三角形ABDと合同になる三角形はどれですか、という問題ですね。
ただし、このように「三角形ABDと合同になる三角形はどれですか」という問題は出題されることはありません。
本番の試験では、いきなり「角アの大きさは何度ですか?」と問われるはずなので、そのスタイルで考えましょう。

角アの大きさを求めるといっても、どこから目をつけていいか分からないわ。

そうですよね。でも、角アを求めるには、どの角の大きさが分かればいいか、を考えればいいですね。

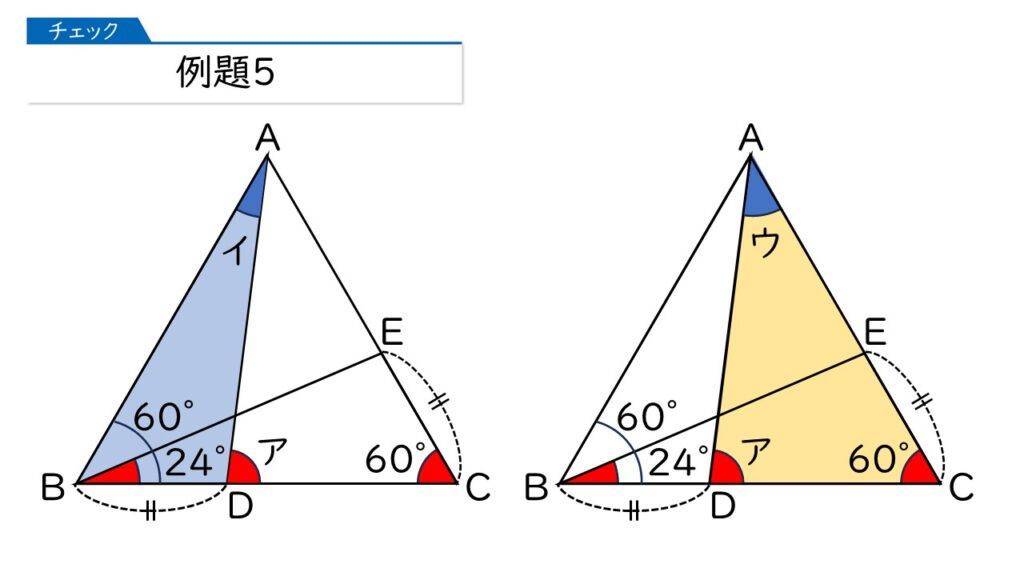
なるほど。左の青色の三角形だと、イの角度が分かれば、三角形の外角で「ア=60+イ」ですね。
右の黄色の三角形だと、ウの角度が分かれば、三角形の内角の和で「ア=180-60-ウ」ですね。

そうです、その通りです。ここで、角イが24°じゃないかな~、ってひらめくとすぐに答えがでますね。
そこで、「三角形の合同」の話になるんです。下の図を見てください。

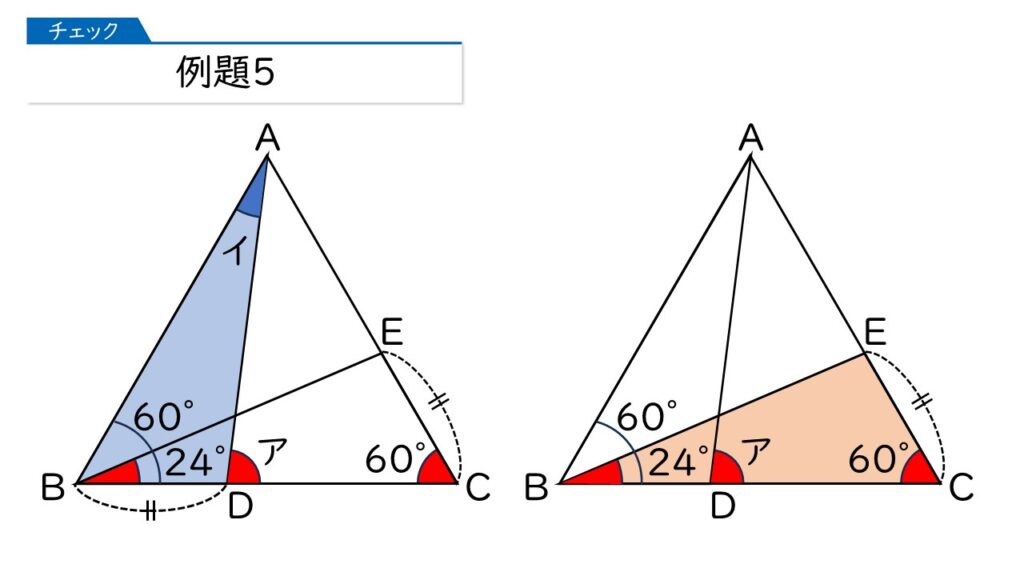
左の青色の三角形と右の赤色の三角形が合同になれば、角イは24°ってわかるんですけど、この二つの三角形は合同になりますか?

そうねぇ~、なると言われればなるかもしれないけど。

じゃぁ、下の図のように、分かっていることを図に書き加えるとどうでしょう?

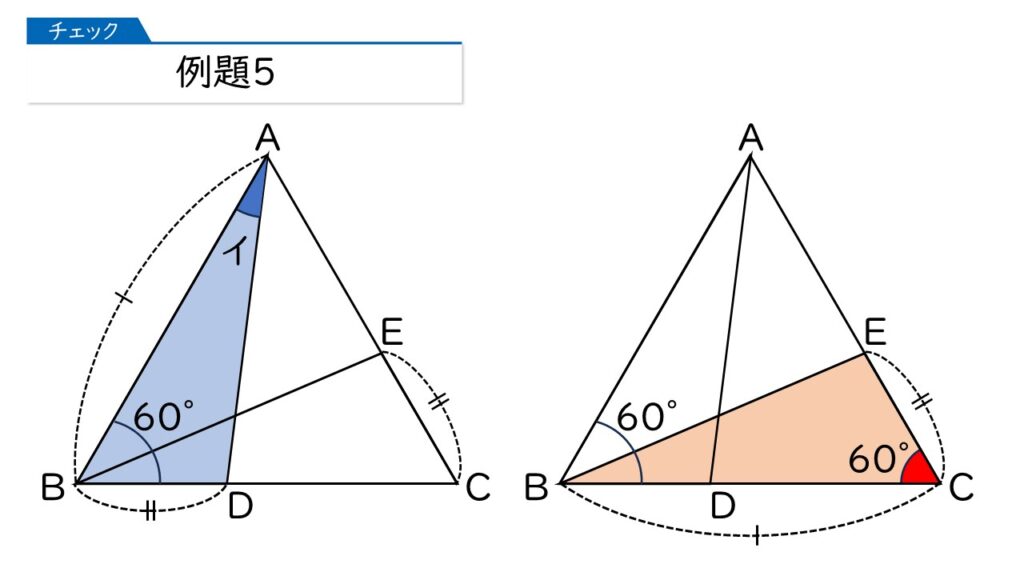
なるほど、この二つの三角形は「2辺とその間の角が同じ」だから、合同になるのね!

そうですね! そこまで言えれば、自信をもって解答できますね。

予習シリーズ算数 図形の面積 例題5(2)
(1)で合同になる三角形が見つかれば、(2)はすぐに答えがでますね。


もう、カンタンだわ。60+24=84°ですね!

大正解です、おめでとうございます!

予習シリーズ算数 図形の面積 例題6
いよいよ最後、例題6です。あと少しですから、もうひとふん張りしましょう!

はい、私は平気ですよ!

下の図は、おうぎ形の中に直線を3本引いたものです。ぬられた部分の面積を求めましょう。

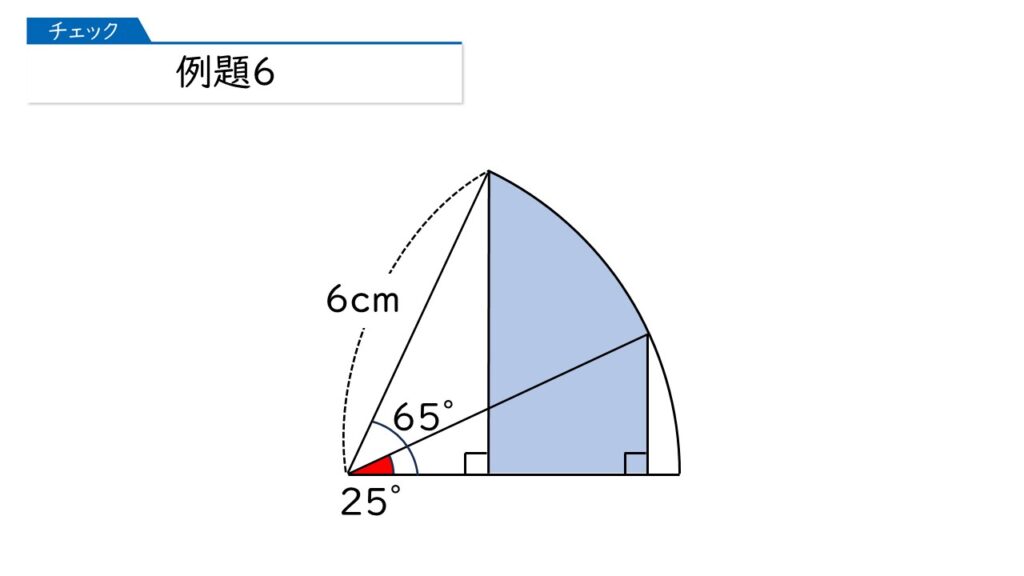
またまた、変な図ね!こんな形の図形の面積なんて、求めることができるのかしら。

これは有名すぎる問題ですね。「面積のうめ替え」を利用することで、ぬられら部分の図形を単純な図形にすることができますよ。

おもしろそう! どのようにすればいいの?

下の図を見てください。求めることができる角度や辺の長さを書き込みました。左と右の直角三角形はどのような関係にありますか?

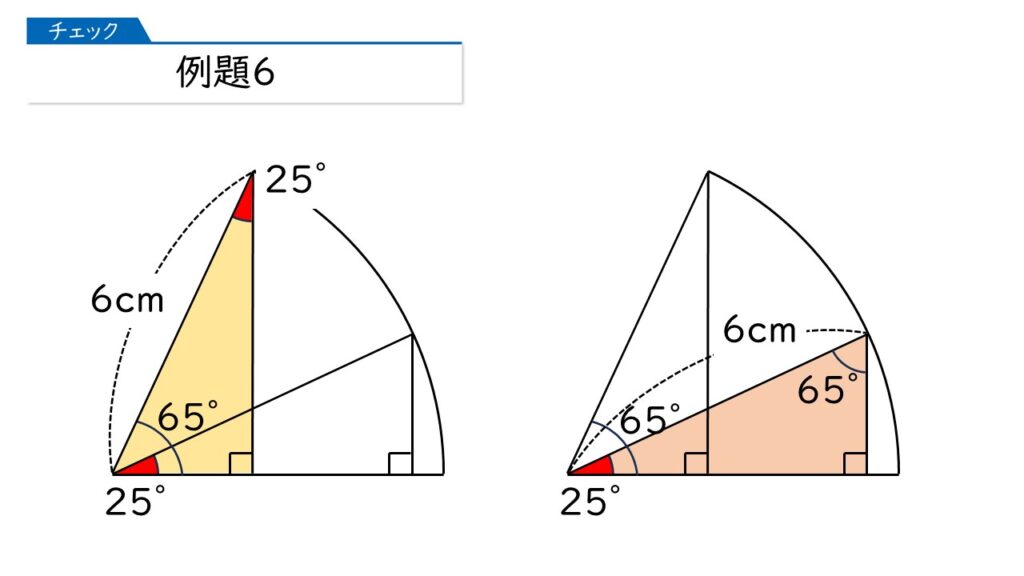
「1辺とその両はしの角度が同じ」だから、この2つの三角形は合同なのね!

よく気づきましたね! この2つの三角形が合同だから、面積も同じになります。
そうすると、下の図で、この2つの三角形が重なっている部分の面積は同じなので、その面積を引いた残りの部分、つまり、★印をつけた黄色の三角形と赤の四角形の面積が同じになりますね。


なるほど! 面積が同じならば、うめ変えることができるってことね。

その通りです! 同じ面積をうめ替えると、下の図で、左の黄色の図形(おうぎ形)の面積と、右の青色の図形の面積が同じになるわけです。

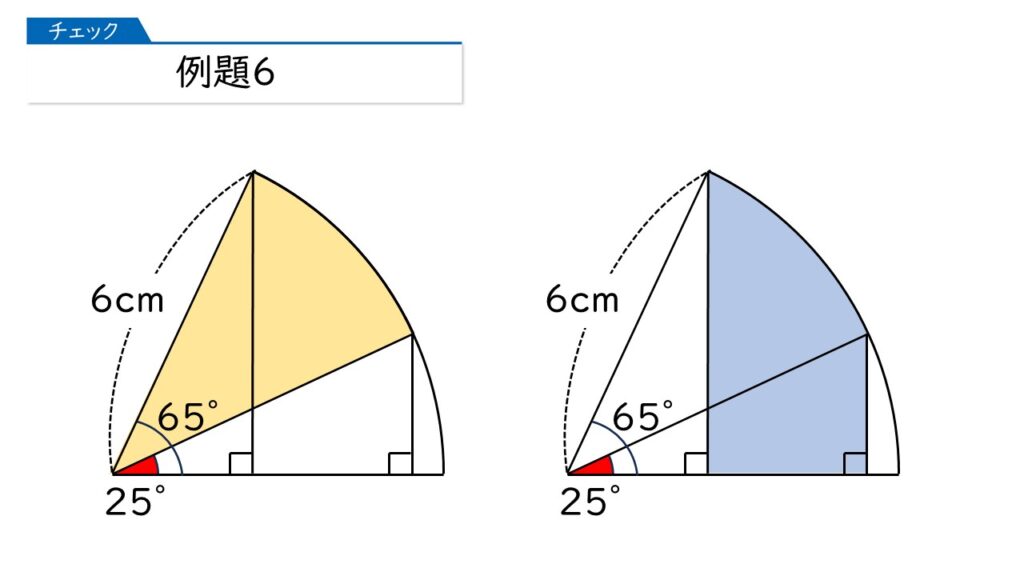
意外とカンタンなのね! 答えは、6×6×3.14×$\dfrac{40}{360}$=12.56(cm2)って出たわ。

正解です、おめでとうございます! 今回もよくがんばりましたね。

重要問題の追加
「予習シリーズ算数 小5前期 第2回 図形の面積」の例題を解説しました。
ただ、他の塾がやっている重要問題がいくつか抜けています。具体的には、次の内容です。
- 面積ではありませんが、「多角形の内角と外角」
- 30°、60°、90℃の定規の辺の比を使った面積の求め方
- いろいろな円の面積の求め方
これらの内容は、下の動画で解説しています。

そんなにできるかな~

でも、このような内容の問題が実際に入試で多く出題されていますから、いずれやらなければいけませんよ。

そうですか。じゃぁ、塾も学校もない日にやってみるわ。

はい、お願いします! 分からないところがあったら、下のフォームから質問してくださいね。








