四谷大塚 予習シリーズ 算数 徹底解説 5年上第3回 割合の利用-クイックラーニング

今回は、予習シリーズ算数の5年上第3回「割合の利用」を徹底解説しますよ。

割合といえば、食塩水や売買とか、ほかにもいろいろな重要問題がありますね。

そうなんです! 割合は、速さや図形と並んで、中学受験算数の最重要分野です。今回は腰をすえてがんばりましょう。


予習シリーズ算数 割合の利用-百分率と歩合
「割合」ってよく耳にしますけれども、どのような意味だと思いますか?

「割合」って、よく耳にはするけど、うまく言い表すことは難しいわ。

そうですよね。下の図を見てください。


4000円をもとにしたとき、1500円の割合は$\dfrac{3}{8}$になります。
つまり、もとにする量をどれだけ大きくしたり小さくしたのか、っていうのが「割合」なんですね。
「割合」は分数や小数で直接表すことができますが、このほかにも、百分率(全体を100としたときの割合)や歩合を使うことがあります。
百分率(ひゃくぶんりつ)と歩合(ぶあい)の使い方は、下の動画で解説してますので、ぜひ、確認してください。
プリントは下からダウンロードして、43ページを見てくださいね。(このプリントは「進学塾アカデミーワン」のオリジナルプリントです。全問題に動画解説をつけていて、塾生はこれで学んでいます。)
算数テキスト (414 ダウンロード )
予習シリーズ算数 割合の利用 例題1
予習シリーズ算数 割合の利用 例題1(1)
さぁ、ここからが本番です。


「6人は、40人の何%ですか。」ということは、つまり、「40人という数をどれだけ小さくしたものが6人ですか」という意味ですね。

そうすると、6÷40=0.15 が答えね。

問題は「何%ですか」ですから、0.15を100倍して15%が正解ですよ。

予習シリーズ算数 割合の利用 例題1(2)
次に、(2)をやってみましょう。


問題文で、「~の」というところが「×(かけ算)」になることがポイントですね。

なるほど。そうすると、2×0.24=0.48L 答えね。

問題は「何mLですか」ですから、単位を 2L=2000mL に直してから計算しましょう。

そうだったわ。問題文をよく読まなきゃ。2000×0.24=480mL が正解ね。

予習シリーズ算数 割合の利用 例題1(3)
(3)に進みましょう。問題文で、「~の」というところが「×(かけ算)」になることがポイントですね。


この問題では「もとになる数」を求めるのね。「もとになる数×割合=比べられる数」だから、もとになる数は「比べられる数÷割合」で出せるわ。
そうすると、正解は 540÷0.45=1200円ね。

そうですね、正解です! それでは、ここまでの基礎を使って、例題2をやってみましょう。

予習シリーズ算数 割合の利用 例題2
予習シリーズ算数 割合の利用 例題2の解き方
割合の問題では「求める数を①」とおくことがポイントです。この問題では「全体のページ数を①」とおくことになります。①を「マル1」と呼びます。
では、式を立てて解いてみましょう。


この式のように、問題文を読みながら、割合を使って式を立てましょう。この式は、下の図のようにして考えます。

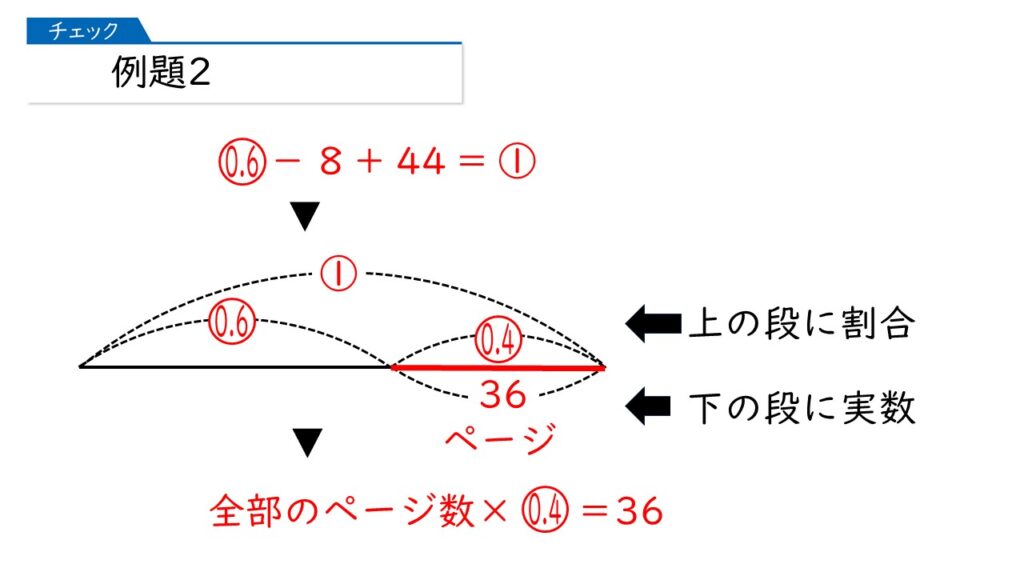
なるほど。そうすると、答えは 36÷0.4=90ページですね!

その通りです!

マルイチ算はとても重要<練習問題ダウンロード>
なんか、中学でやる方程式みたい。

そうなんです。算数でよく使う①というのは、方程式の $\large\it{x}$ と同じ役目なのです。つまり、方程式で $\large\it{x}$ とおくところを算数では①にするんです。
この考え方は、比を扱う問題に有効で、年齢算、相当算、倍数算、消去算はほぼこの考え方で解くことができます。

小学生がここまでやるんですね!

一見すると難しい計算なのですが、慣れてしまえば強力な武器になりますので、ぜひ身につけて欲しいですね。
そこで、練習プリントを用意しました。3枚ありますので、ぜひ、マルイチ算の計算方法を体得してください。
マルイチ算練習問題 (376 ダウンロード )
予習シリーズ算数 割合の利用 例題3
予習シリーズ算数 割合の利用 例題3の解き方
次は【例題3】です。【例題2】と同じように、問題文から式を導き出しましょう。ここでも、求める数を①とおきます。


そうすると、「=」を使って式が立ちますね。


なるほど。そうすると、答えは 18÷0.15=120人ですね!

正解です! よくできましたね。

線分図はかくべきかどうか
ここまで線分図を書いてきたけど、いつも線分図を書かなければいけまないの?

それって重要なギモンですよ。式の意味を理解するには、線分図を使ったほうがいいです。
ただ、【例題3】まではほとんどの子どもが解けるんですけれども、【例題4】以降になると解けない生徒が激増します。
なぜかっていうと、線分図が複雑になって、自分では書けなくなるからなんです。

でも、塾の先生は線分図で説明するから、そうするしかないんじゃないかしら。

そうですね。
ただ、予習シリーズにあるように、全体をつかむようなカンペキな線分図は、情報が多すぎて、かえって子どもにはわかりずらいこともあります。
「線分図を完成させること」を目的とせず、「問題のどこに注目すれば解けるか」に注目させることが大事です。
そのような視点で、次の問題に進みましょう。

予習シリーズ算数 割合の利用 例題4
予習シリーズ算数 割合の利用 例題4の解き方
問題文を読んで、着眼点を探しましょう。


この問題では「残りの所持金がいくらか」が分かればカンタンに解けます。下の図を見てください。

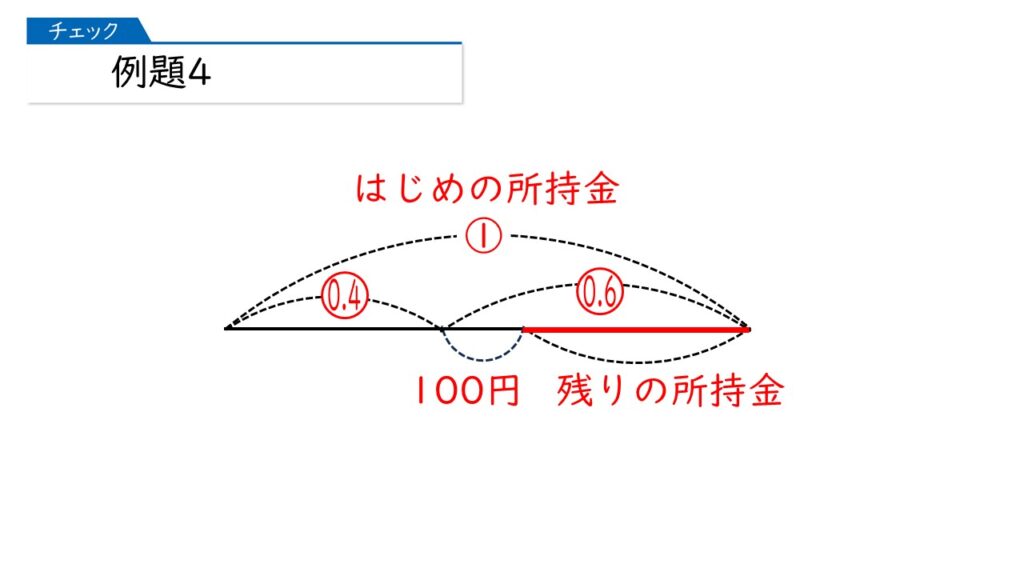
なるほど!「 (100+残りの所持金)÷0.6」で答えが出せる、ってわけね。

そうなんです! 線分図で「全体像」を書かせると、いろんな数が入り乱れて混乱してしまうんですね。
ですから、突破口を子どもに示すことが非常に重要なんです。問題が難しいから解けないのではなく、難しい解き方を教えるから解けないことがあることを知って欲しいですね。

残りの所持金は次のように求めることができます。①の割合とは基準が違うので、1 を使いますよ。

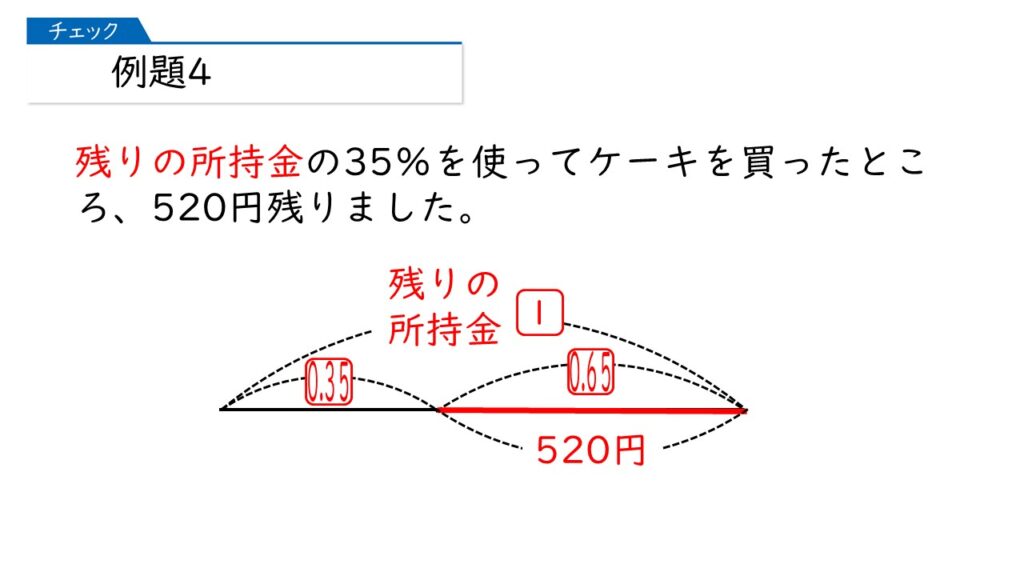
残りの所持金は、520÷0.65=800円ね!

そうです! よくできましたね。そうしたら、もう答えが出ます。

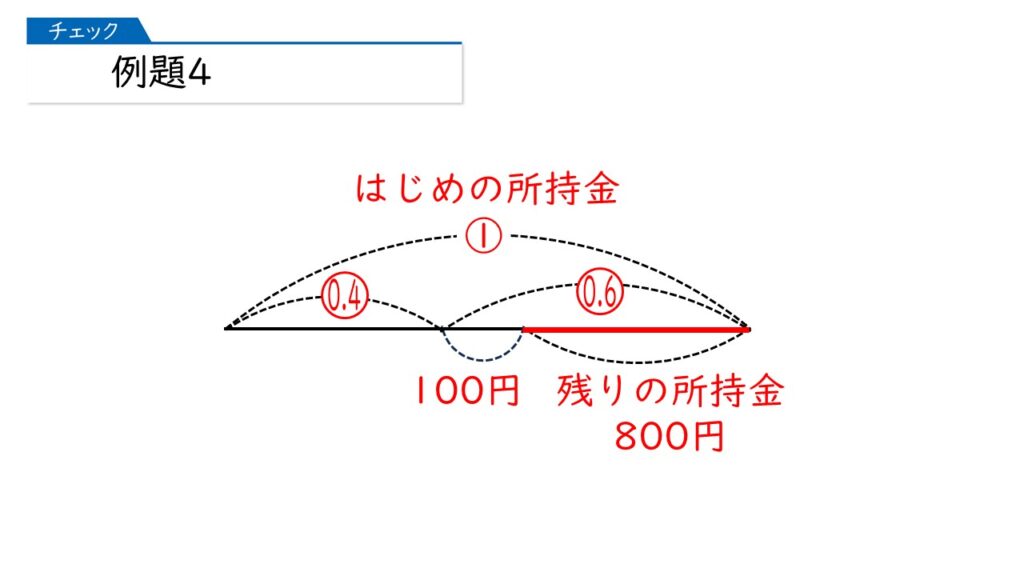
(800+100)÷0.6=1500円が答えですね!

はい!

予習シリーズ算数 割合の利用 例題5
予習シリーズ算数 割合の利用 例題5の解き方
【例題5】に進みましょう。カンタンですから、落ち着いて考えましょう。まずは、問題文を読んでください。


ポイントは、1日目、2日目、3日目に読んだページ数の割合を、本全体のページ数をもとにして表す、ということです。


なるほど。 3日目に読んだページ数の割合を、全体をもとにした割合に直せばいいんですね。

そうです!もとになる数をそろえることで、1日目から3日目の割合を足すことができるようになります。


4日目のページ数が分かっていますから、全体をもとにしたときの4日目の割合が分かれば、答えを出すことができます。


すると、答えは 39÷$\dfrac{13}{60}$=180ページってことね!
でも、計算が複雑ね。

予習シリーズ算数 割合の利用 例題5のカンタンな別解
割合が分数のときは、登場するすべての分数の分母の最小公倍数をもとめて、それを全体(もと)にすれば、計算がラクになりますよ。
この問題では、3と5と4の最小公倍数である60を全体(もと)にします。


なるほど! こっちのほうが計算がカンタンね。

このやり方は、仕事算やニュートン算でも使えますよ!

予習シリーズ算数 割合の利用 例題6
ここまできましたね。【例題6】もできるようにしましょう! まずは問題を見てください。


こんなの絶対に解けないわ…

大丈夫、【例題5】の別解を使えば、カンタンに解けますよ!
この問題文に登場する分数の分母(3と4と6)の最小公倍数は12ですから、全体を⑫とおきます。


そして、「$\dfrac{1}{3}$よりも4個多く取り出した」と書いてありますが、「$\dfrac{1}{3}$」の残りの割合もしっかり意識することが重要です。
そうすると、兄が取り出した時点での線分図は次のようになります。

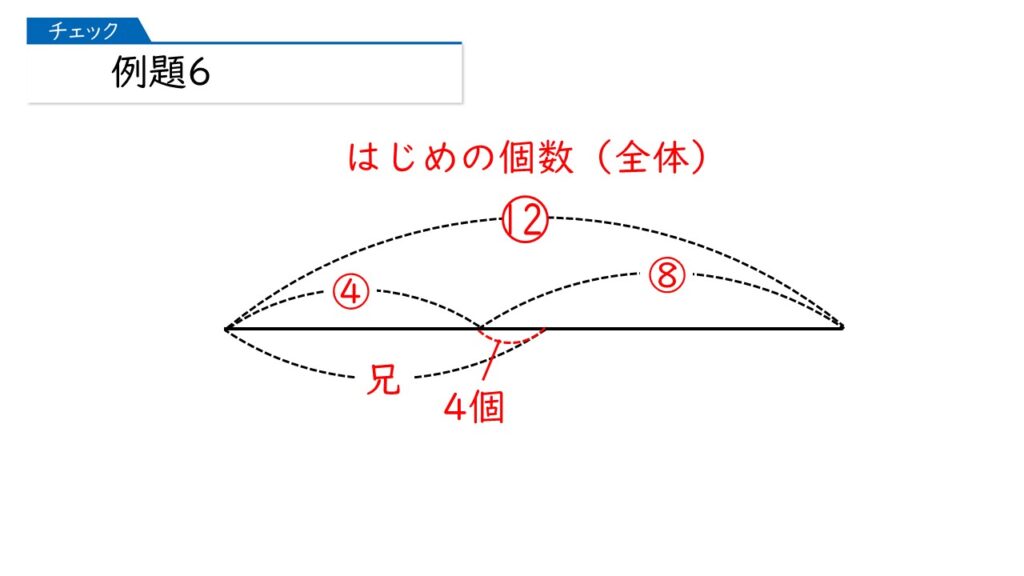
この図に、弟が取り出した後のようすを書き出していくことになります。


ここで、兄が取った残りを新たな割合で考えると、とても難しい問題になってしまいますので、やめてください。
兄が取り出した後のアメの個数の割合は、(⑧-4)ですから、弟が取り出したアメの個数の割合は、(⑧-4)×$\dfrac{1}{4}$に5を加えて、(②-1+5)になります。


そして、最後に残ったアメの個数は、「はじめの個数の$\dfrac{1}{6}$」、つまり、⑫×$\dfrac{1}{6}$=②となります。

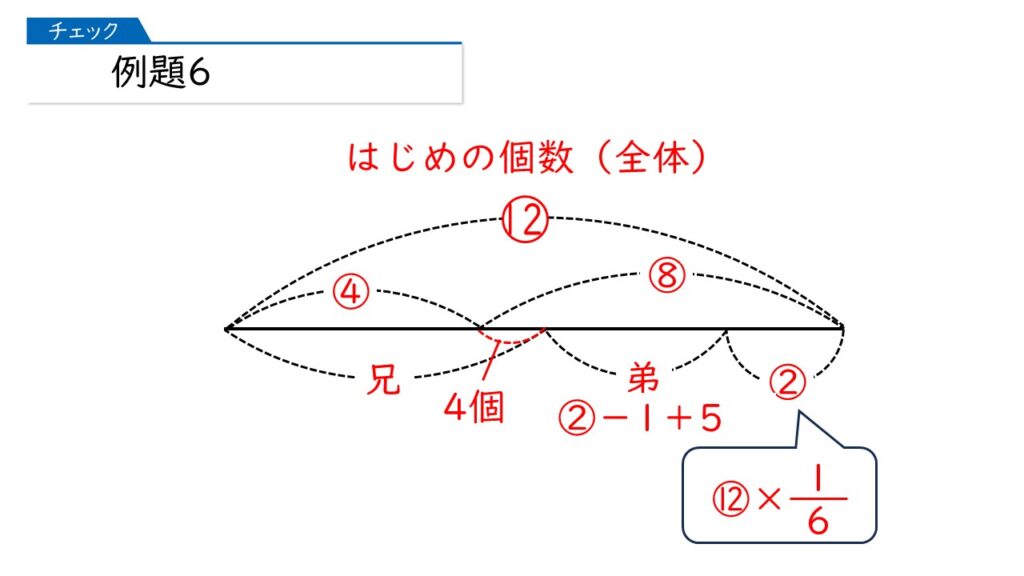
そうしたら、下の図のように、シンプルな線分図が完成します。赤線の部分に注意すると、マルイチ算の計算方法で答えが出ますよ。

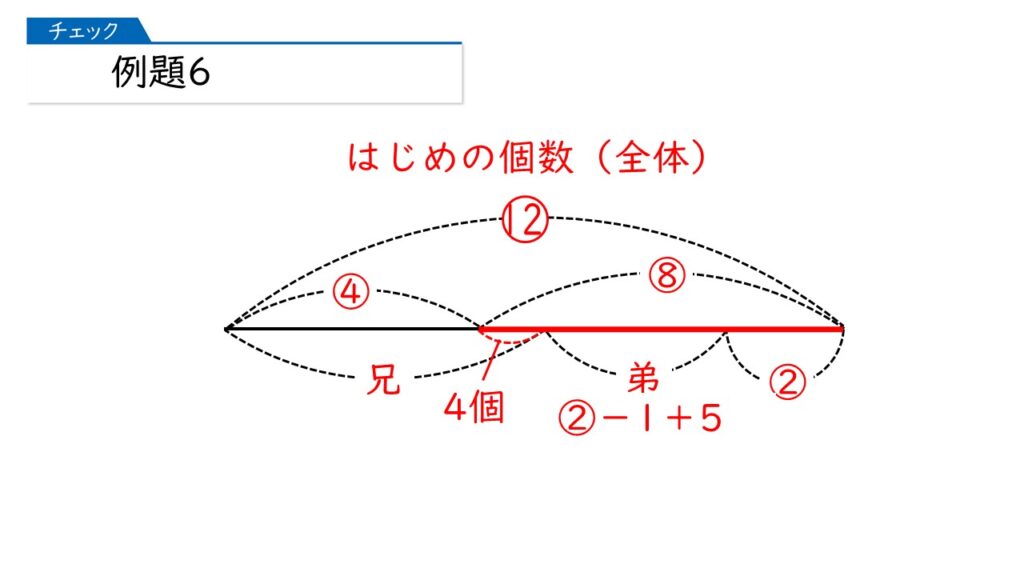
なるほど! ⑧=4+②-1+5+② になるわけね。

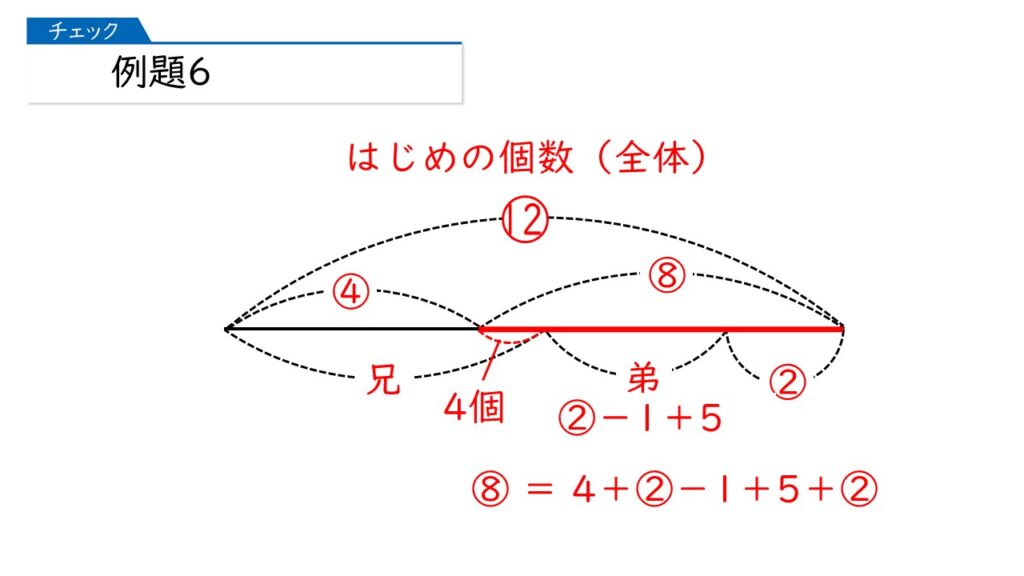
その通りです! 計算できるところを計算すると、「⑧=④+8」になりますから、④=8、①=2になります。

全体(もと)の割合が⑫だから、答えは、⑫×2=24ページってことね。

よくできました! 予習シリーズの解法を見るとアタマが痛くなる人も、これであれば解けそうですね。
ぜひ、類題もやってみてください!

予習シリーズ算数 割合の利用 例題7
【例題7】のような「やりとり問題」は、食塩水のところでよく出題されますね。パターンを知ってしまえば難しくはありません。
さぁ、問題を見てみましょう!


「やりとり問題」が出たら、まず、次のような図を書いて、問題を整理してください。
この問題では「3人が持っているカードの総数が36枚」で、「やりとりが終わった時点で3人が持っているカードの枚数がすべて同じ」なので、最後にA、B、Cはそれぞれ12枚ずつ持っている、ということです。

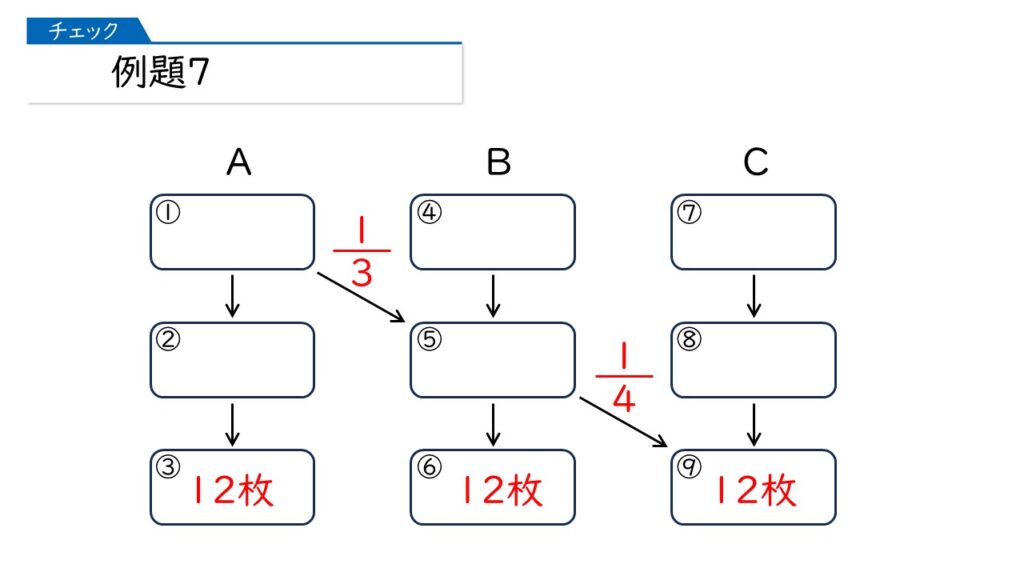
次に、この図の①~⑨の中で、同じ数になるところを埋めていきます。

②と③、⑦と⑧が同じね!

その通りです! この問題では、②と③が同じであることが分かればいいですね。


そうしたら、芋づる式に埋めていきましょう!
⑤の枚数をみると、Bは「持っている枚数×$\dfrac{3}{4}$=12」ですね。
だから、⑤に入るのは16枚です。


そうすると、AがBに渡した枚数が分かれば答えがでるわ。
①の枚数をみると、Aは「持っている枚数×$\dfrac{2}{3}$=12」だから、18枚ですね。

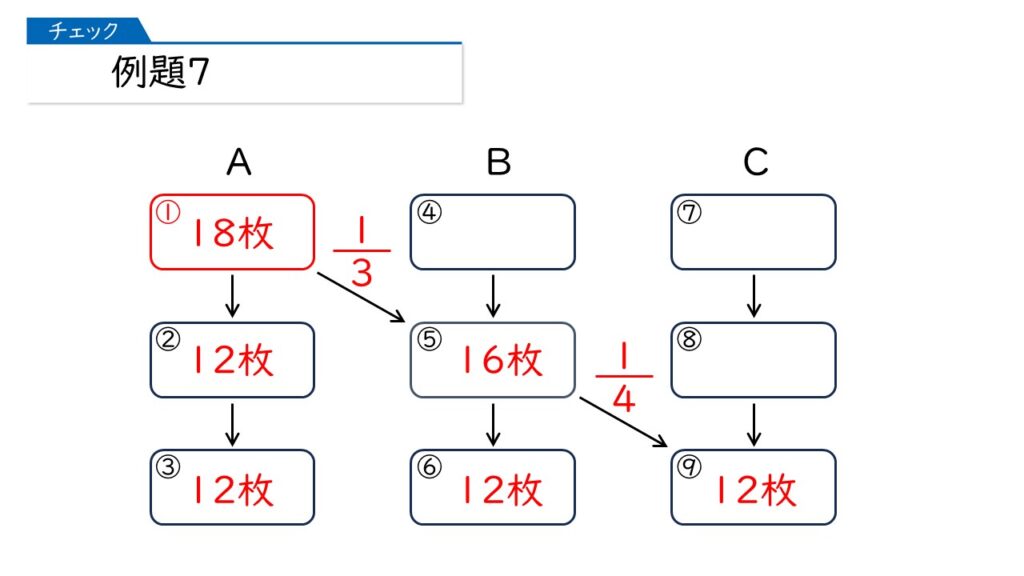
その通りです! あと少しです。④を求めましょう。

AがBにわたしたのは、18×$\dfrac{1}{3}$=6枚だから、Bが初めにもっていたのは 16-6=10枚ね。

よくでしました!

手順をふんでいけば、そんなに難しくないわ。

そうですね! 慣れが必要なパターンですので、何回か練習しておきましょう。
今回もお疲れ様でした。質問がありましたら、下のフォームからお願いします!





第8回.jpg)


