四谷大塚 予習シリーズ 算数 徹底解説 5年上第8回 多角形の回転・転がり移動-クイックラーニング
第8回.jpg)
今回は、「多角形」の回転・転がり移動を見ていきますね。

回転・転がり移動だなんて、何だか楽しそうね。

はい、一度きちんと理解してしまえば、すぐに得意になる分野です。ですが、この分野できちんと得点できる生徒はそんなに多くありません。
得点できない原因は何かをしっかり説明していきますね!



予習シリーズ算数 多角形の回転・転がり移動 例題1
例題1(1)の解き方
まず、例題1(1)から見ていきましょう。下の図で、アの角度を求めます。

第8回-例題1-1024x576.jpg)
ポイントは、三角形ABCが二等辺三角形であることと、頂点Cを中心にして28°回転した、ということです。
この条件から、分かる値をどんどん書き込みましょう!


なるほど、カンタンだわ。条件から、青と赤の角度が分かるから、角アの大きさは、67-28=39°ね。

その通りです! この問題がなぜカンタンに解けたかというと、次の2点に注意したからなんです。
- 問題文から分かる角度を全部書き出している
- 回転する前と後の図を別々に書いている
このようにして、図形の問題は「シンプルに見る」ようにすることが得意になる早道です。

そうだったのね。図形の問題が苦手な人には助かるわ。

例題1(2)の解き方
次に、例題1(2)を見てみましょう。求めるのは、下の図の角イの大きさです。

第8回-例題1-1024x576.jpg)
う~ん、イの角度なんて求めることができるのかしら?

そうですよね、心配になっちゃいますね。では、下の図で分かることはありませんか?

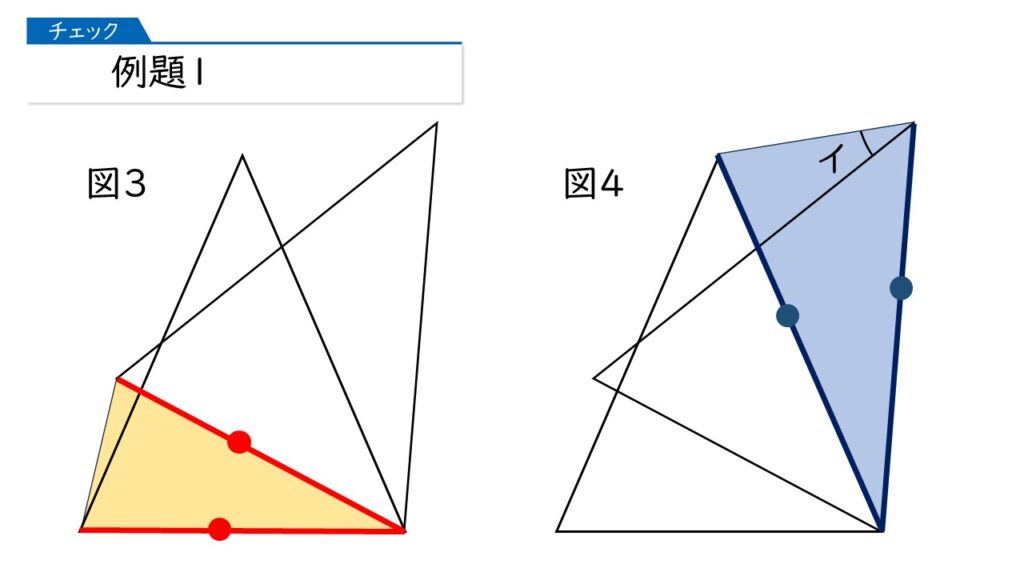
黄色い三角形も青い三角形も「二等辺三角形」ね!

そうです、その通りです! そうしたら、図2と図4を比べてみましょう。何が分かりますか?

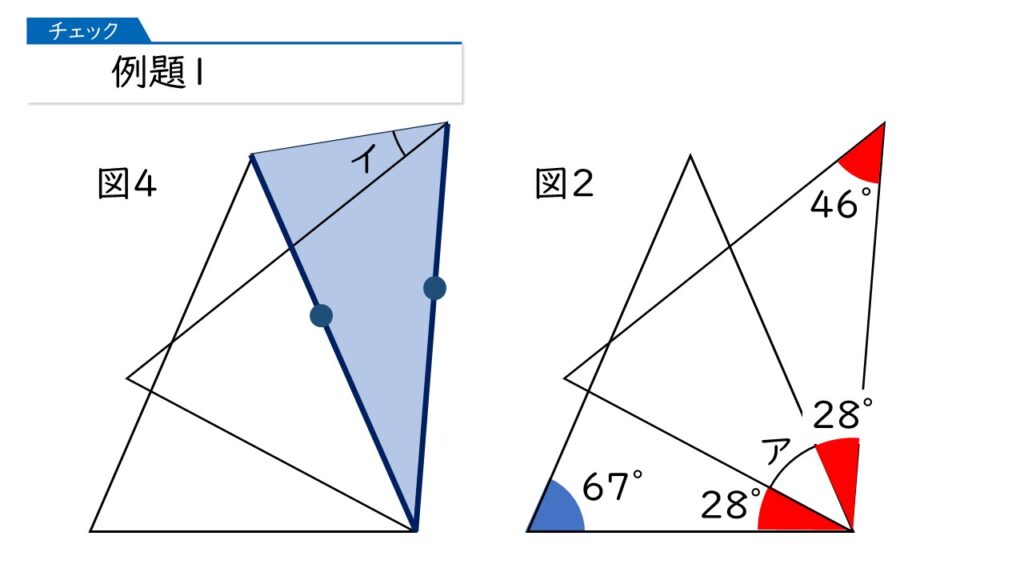
青の二等辺三角形の頂角が28°だから、底角も求められるわ!


図4で、角ウの大きさが (180-28)÷2=76° だから、角イの大きさは 76-46=30° ね!

その通りです! 二等辺三角形の回転移動の問題では、二等辺三角形がたくさんできるって覚えておくといいですね。

予習シリーズ算数 多角形の回転・転がり移動 例題2
例題2(1)の解き方
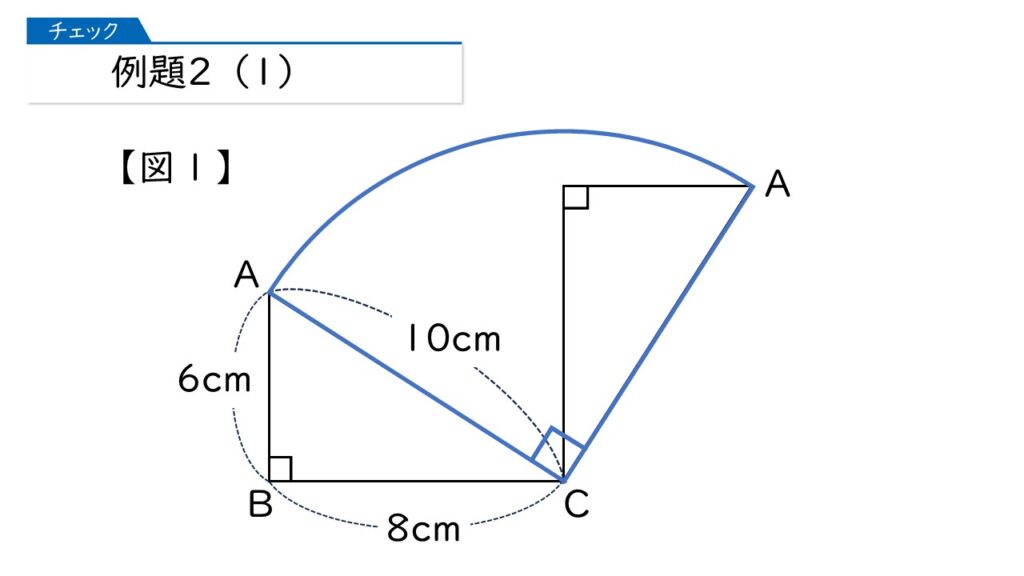
続いて、例題2にすすみましょう。まず(1)です。下の図で、頂点Aが動いたあとの線の長さは何cmになりますか?

第8回-例題2-1024x576.jpg)
これはカンタンね。頂点Cを中心としたおうぎ形の弧の長さになるわ。

その通りです、早いですね!
10×2×3.14×$\dfrac{90}{360}$=15.7(cm)が答えですね。

例題2(2)の解き方
次に(2)です。下の図で、辺ACが動いたあとの図形の面積は何cm2になりますか?

第8回-例題2-1024x576.jpg)
これもカンタンね。頂点Cを中心としたおうぎ形の面積になるわ。


はい、その通りです!
10×10×3.14×$\dfrac{90}{360}$=78.5(cm2)が答えですね。

例題2(3)の解き方
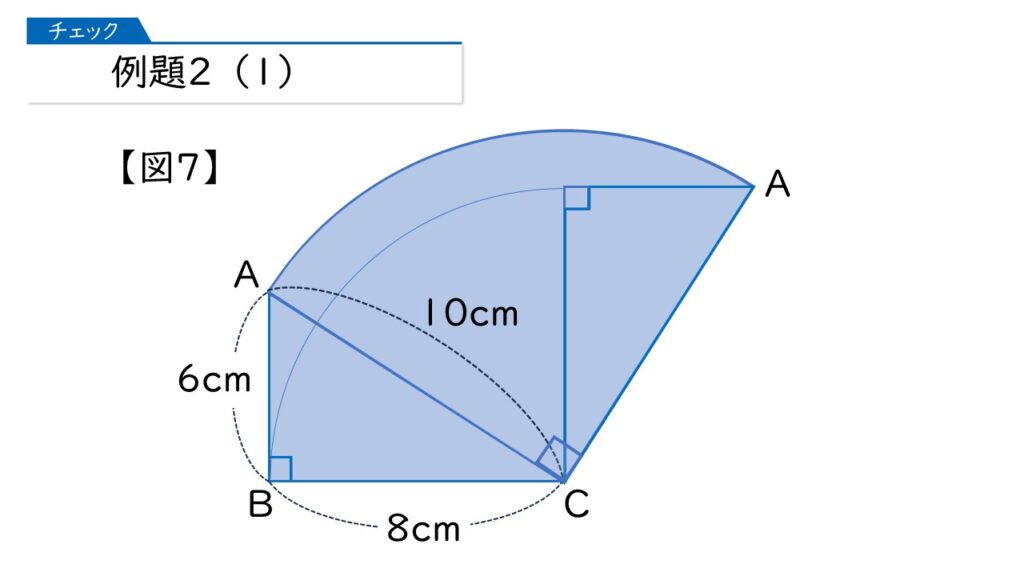
では(3)です。下の図で、辺ABが動いたあとの図形の面積は何cm2になりますか?

第8回-例題2-1024x576.jpg)
出発点と終点はこんな感じね。でも、そのと中はどうなるのかしら。


そう、今回のポイントはそこにあります! と中がどうなっているのかをしっかり自分の手で確かめることが大事です。
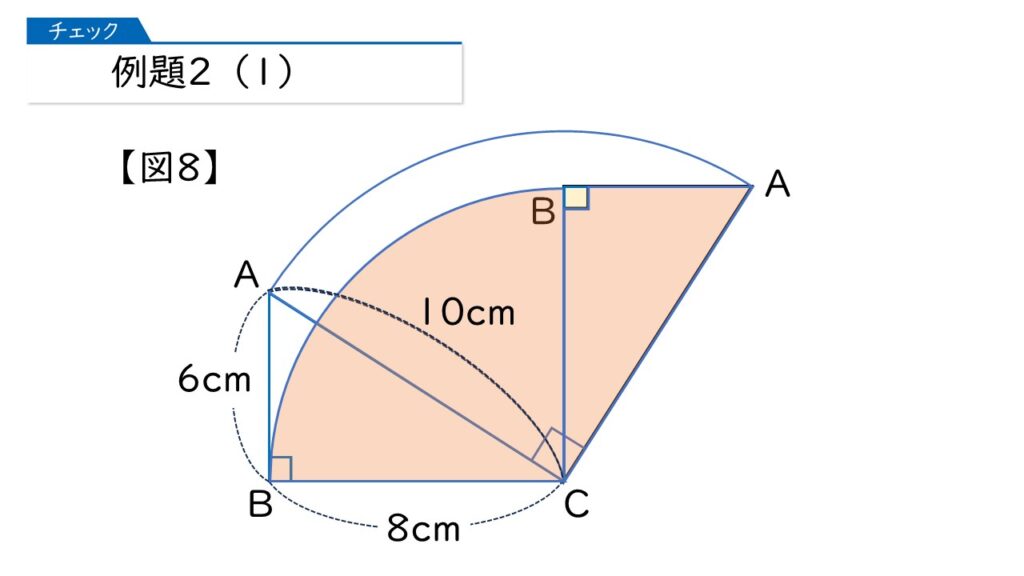
この問題の場合は、下の図のようになっています。

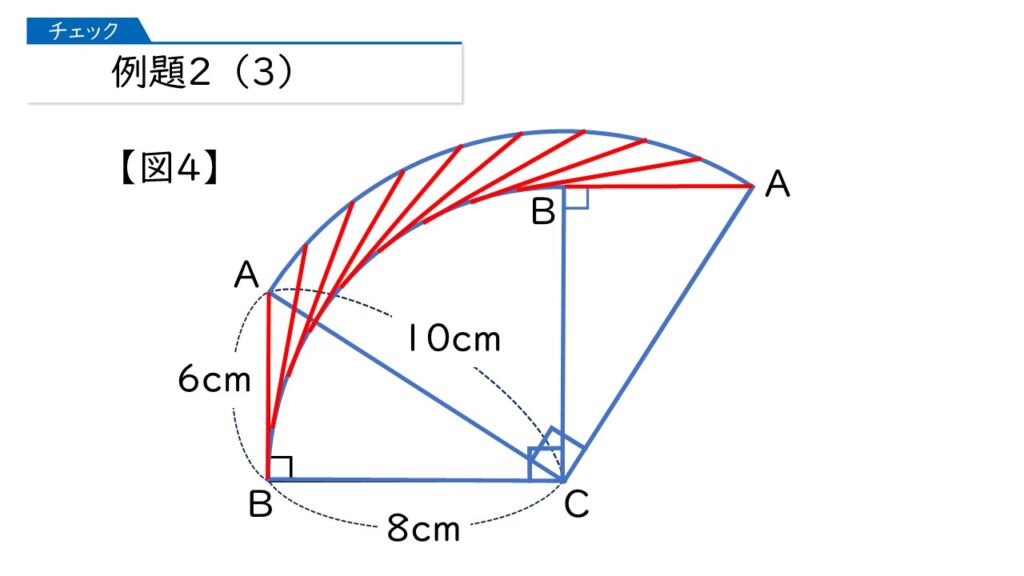
そうすると、辺ABが通ったあとの図形の面積は、下の黄色い部分の面積になります。この面積はどのようにしたら求めることができますか?


変な形ね。こんな図形の面積、どうやったら出せるの?

確かに、慣れてないとなかなか難しいですね。ポイントは、下の青にぬった部分の面積から、ある面積を引けば求めることができます。

分かったわ! 下の赤色の部分の面積を引けばいいのね。

その通りです、よく見抜けましたね! したがって、求める面積は、次のようになります。
10×10×3.14×$\dfrac{90}{360}$+直角三角形の面積-(8×8×3.14×$\dfrac{90}{360}$+直角三角形の面積)
=10×10×3.14×$\dfrac{90}{360}$-8×8×3.14×$\dfrac{90}{360}$
=(100-64)×3.14×$\dfrac{90}{360}$
=9×3.14
=28.26(cm2)

結局、半径10cmのおうぎ形の面積から、半径8cmのおうぎ形の面積を引いた、ってわけね!

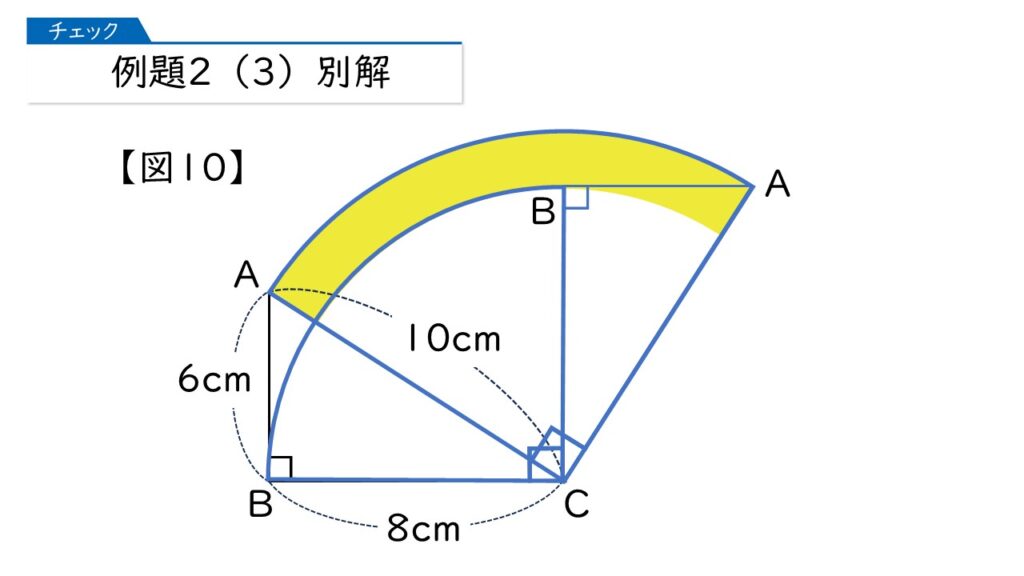
その通りです!同じ式になりますけど、次のような別解もあります。
下の図で、左の赤の斜線部分の面積と、右の赤の斜線の面積は同じになりますから、左の赤の斜線部分を右の斜線部分にうめかえるんです。


なるほど! そうすれば、求める面積は下の図の黄色の部分の面積になるから、初めに求めた式で同じ答えがでるのね。

その通りです。好きな方のやり方で解いてみてくださいね。

予習シリーズ算数 多角形の回転・転がり移動 例題3
例題3(1)の解き方
では、例題3に進みましょう。まずは(1)。下の図で、頂点Cが動いたあとの線の長さを求めましょう。

第8回-例題3-1024x576.jpg)
これはカンタンね。頂点Bを中心とした円の円周の長さになるわ。

その通りですね! 順を追って確認してみましょう。


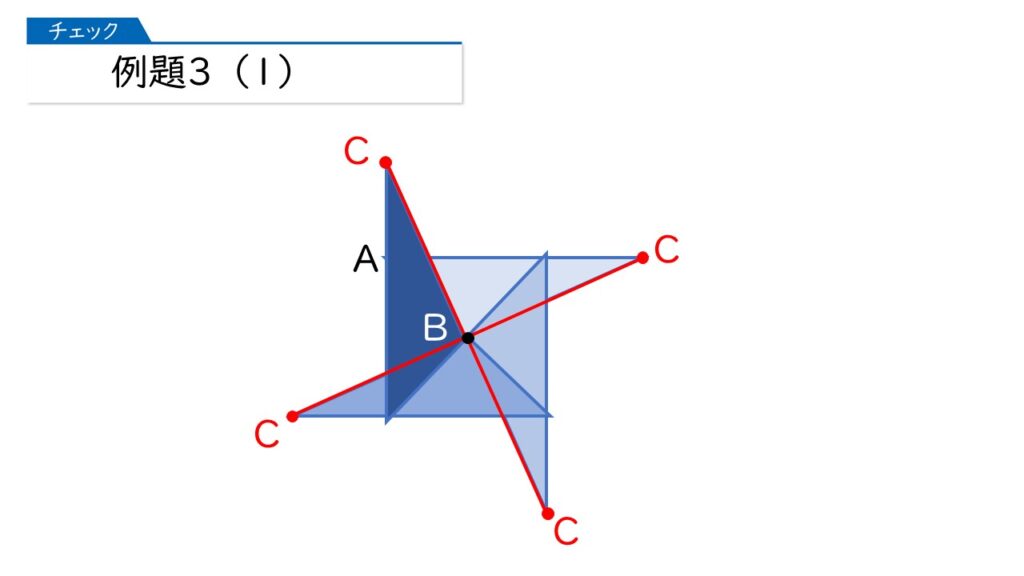
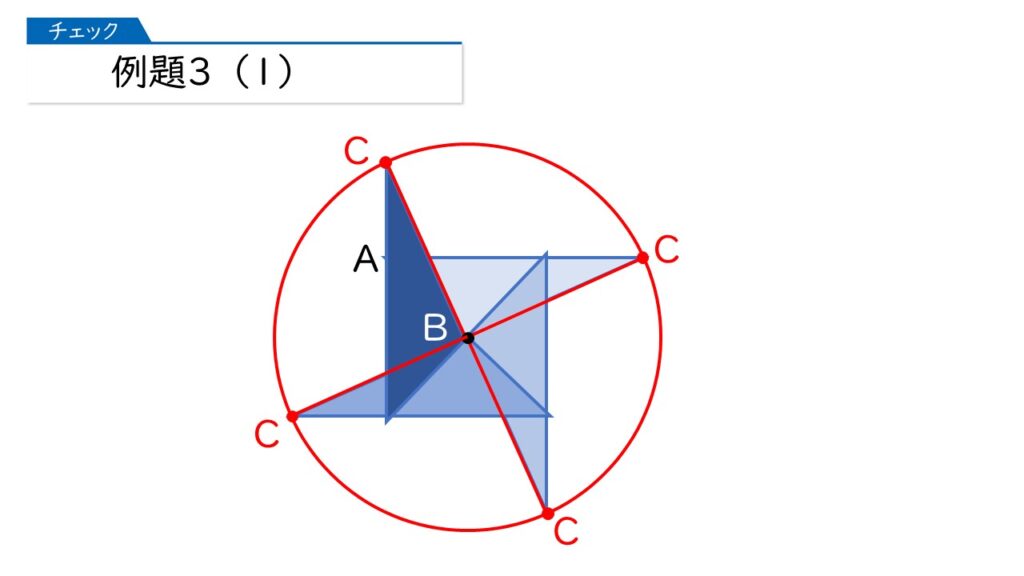
5×2×3.14=31.4(cm)が答えね!

はい、正解です! 迷ったら、と中の図も書くといいですね。

例題3(2)の解き方
では、(2)です。下の図で、辺ACが動いたあとの図形の面積を求めましょう。

第8回-例題3-1024x576.jpg)
Bを中心に回転するけど、頂点Aも頂点Cも中心Bからはなれているわね。予想がつかないわ…

そうですね。でも、少しずつ動かしてみると、見えてきますよ。では、10°ずつ動かしてみますね。


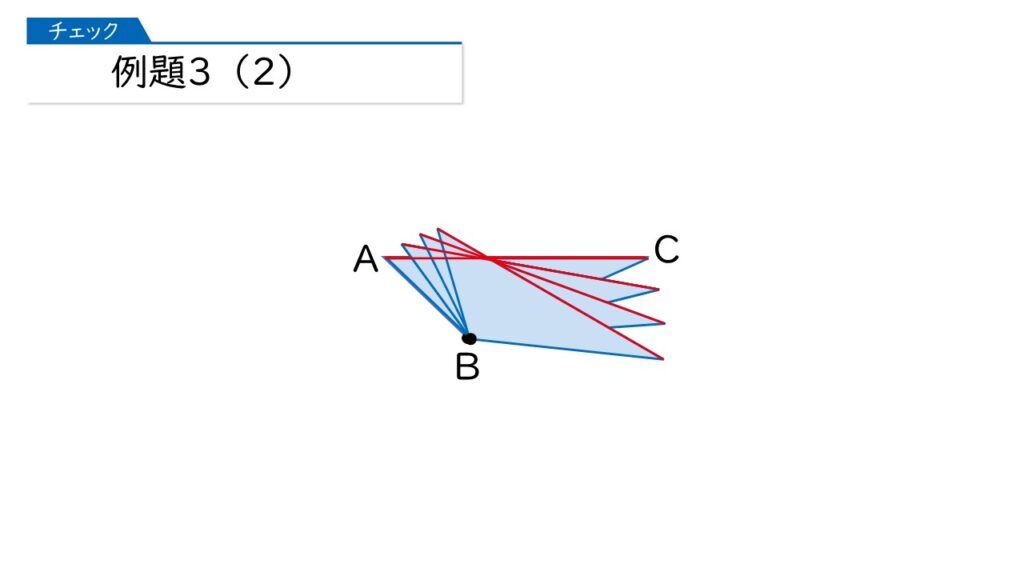
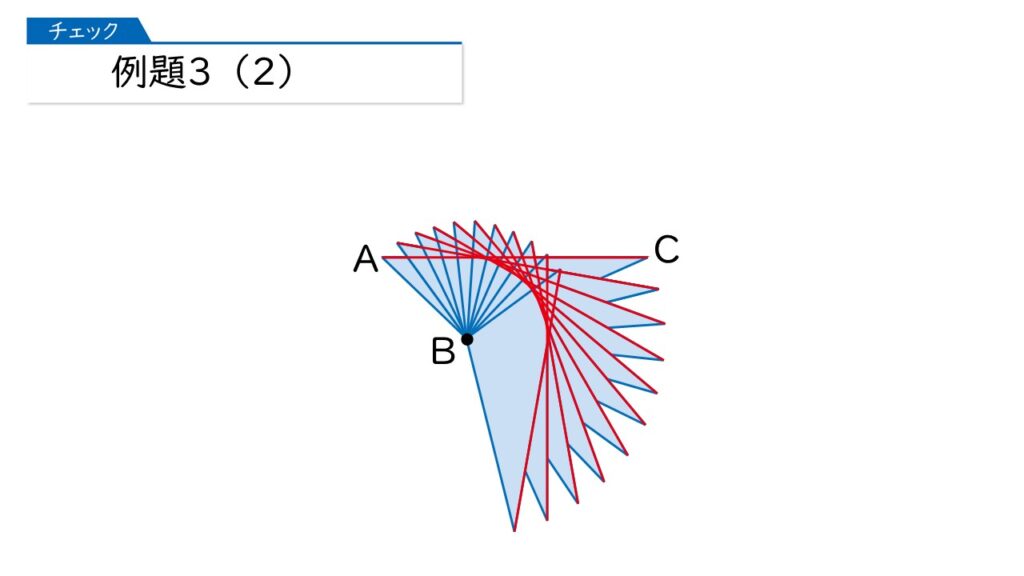
どうですか、見えてきましたか?

ん~、まだ分からないわ…

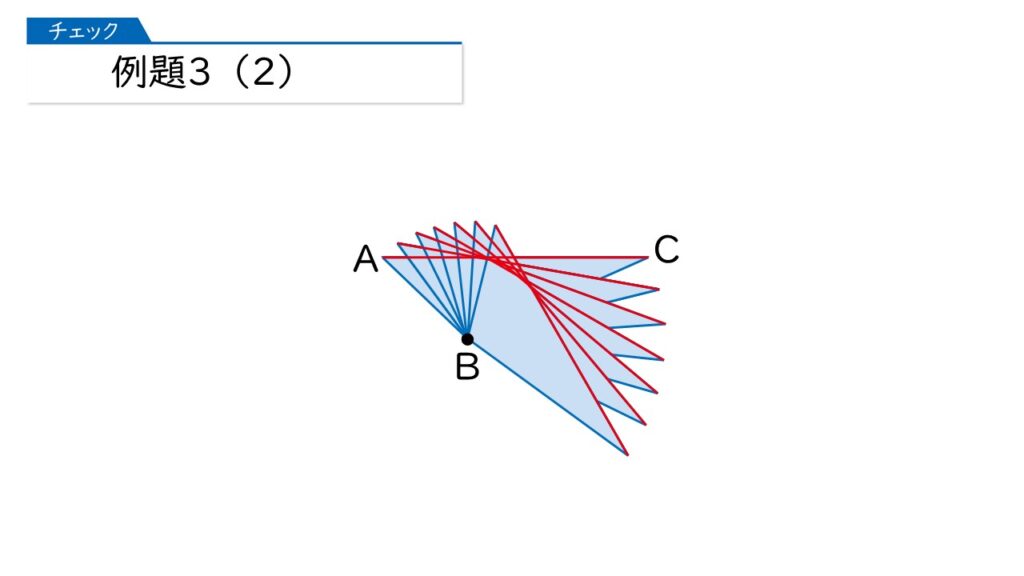
分かりました。もっと動かしてみますね。

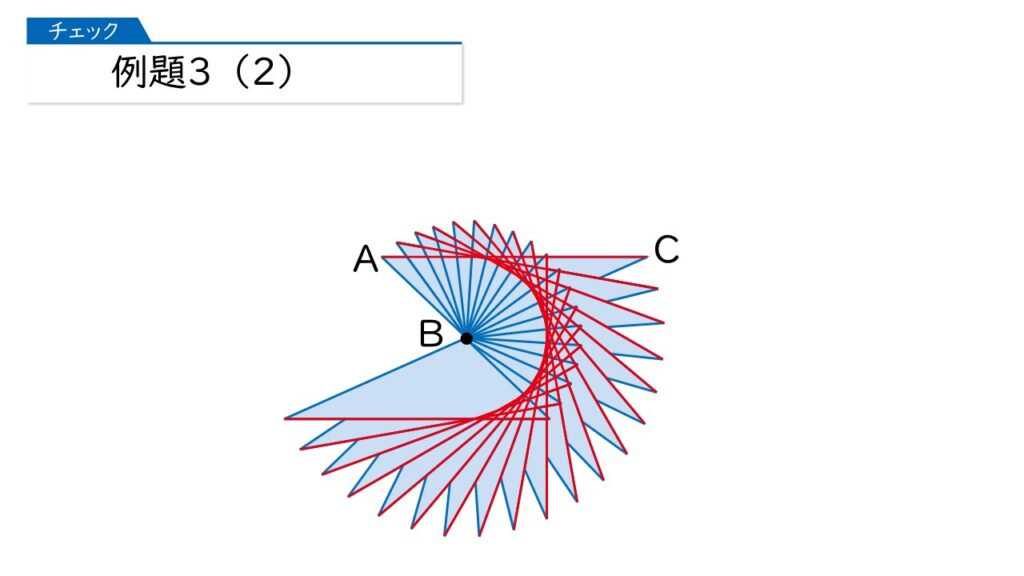
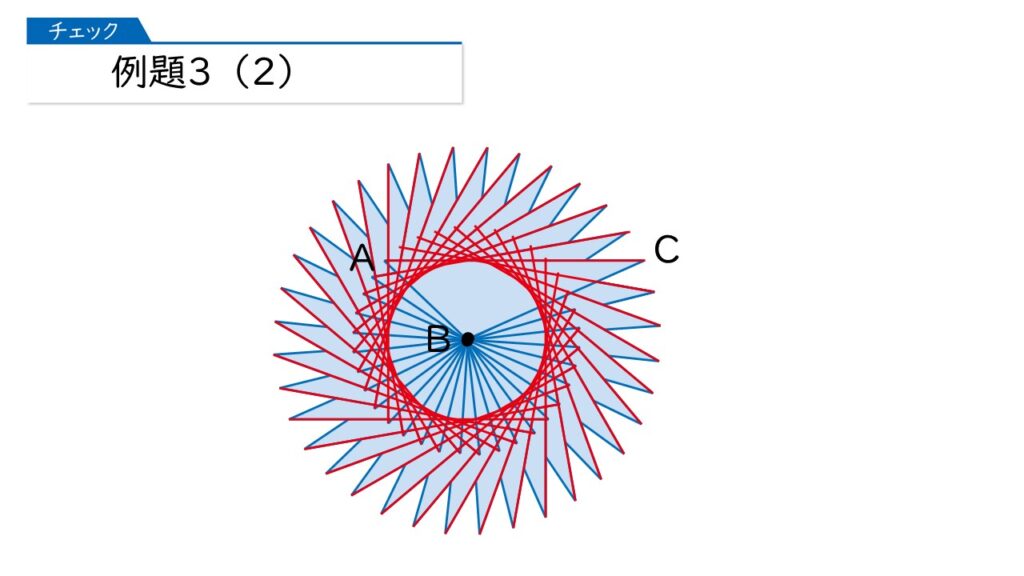
分かったわ! ドーナツ型になるのね。

その通りです! 手を動かして、と中のようすを書くことが大事です。


そすすると、下の図のようなドーナツ型の面積を求めればいい、ということがわかります。

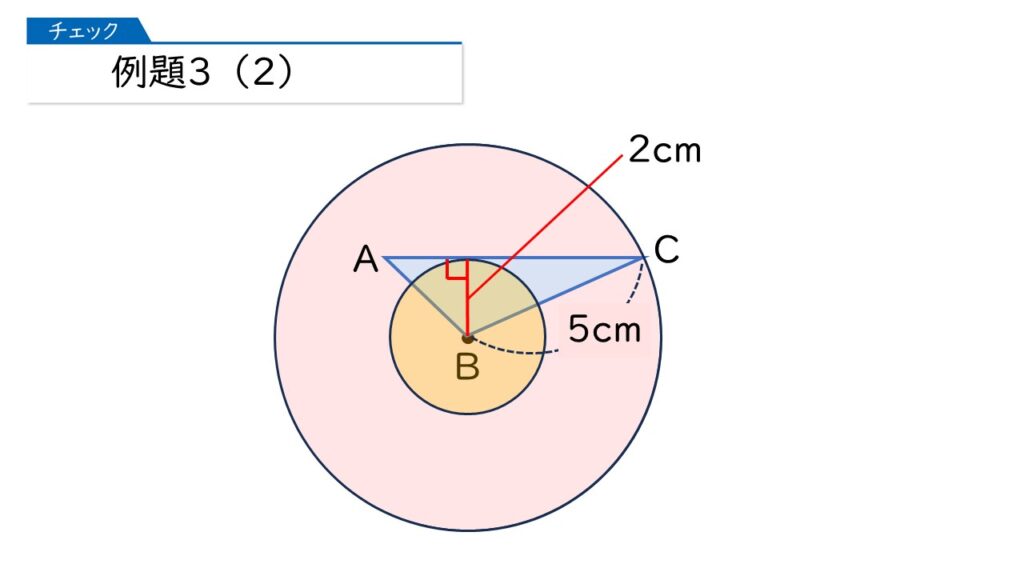
5×5×3.14-2×2×3.14=(25-4)×3.14=65.94(cm2)が正解ね!

その通りです! 回転する図形の中でも、回転の中心が動かない問題は難しくありませんね。

予習シリーズ算数 多角形の回転・転がり移動 例題4
例題4(1)の解き方
次に、例題4です。例題4は(1)と(2)がありますが、両方一気に解いちゃいますね。
(1)下の図で、頂点Bが動いたあとの線の長さを求めなさい。
(2)下の図で、頂点Bが動いたあとの線と直線ℓで囲まれた図形の面積を求めなさい。

第8回-例題4-1024x576.jpg)
めんどくさそうで、やりたくないわ…

お気持ちは分かります。できればやりたくないですけど、中学受験で「図形の移動」は頻出分野なので、がまんしてやりましょう。
まず、90°ずつ動かしていきましょう。はじめ、頂点Cを中心に90°動かしますが、そのとき、その他の頂点D、A、Bがそれぞれどのように動くかを、自分の手と目で確かめることが重要です。
では、まず頂点Dが動くようすを書きましょう。

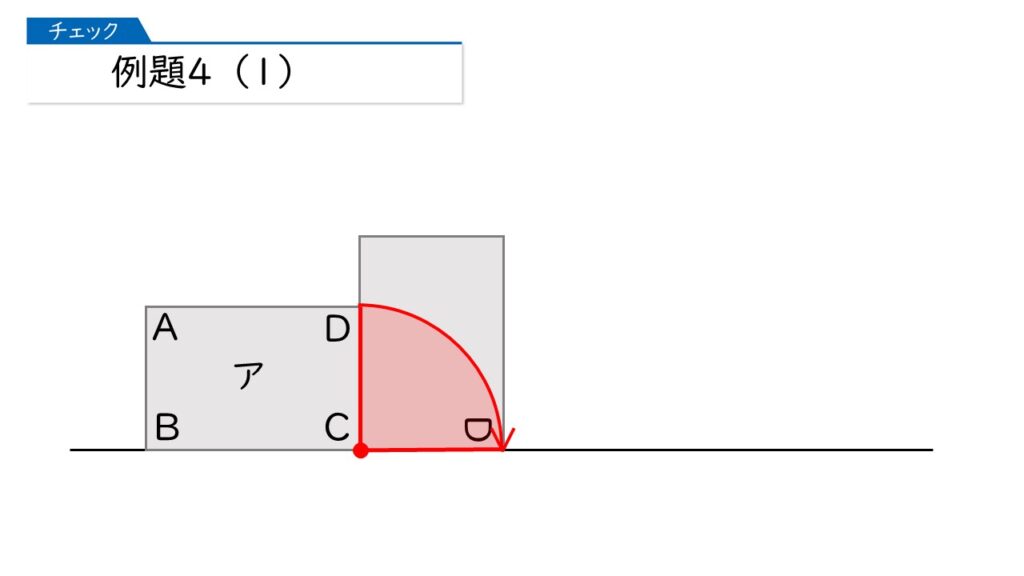
このとき、頂点Aは次のように動きます。

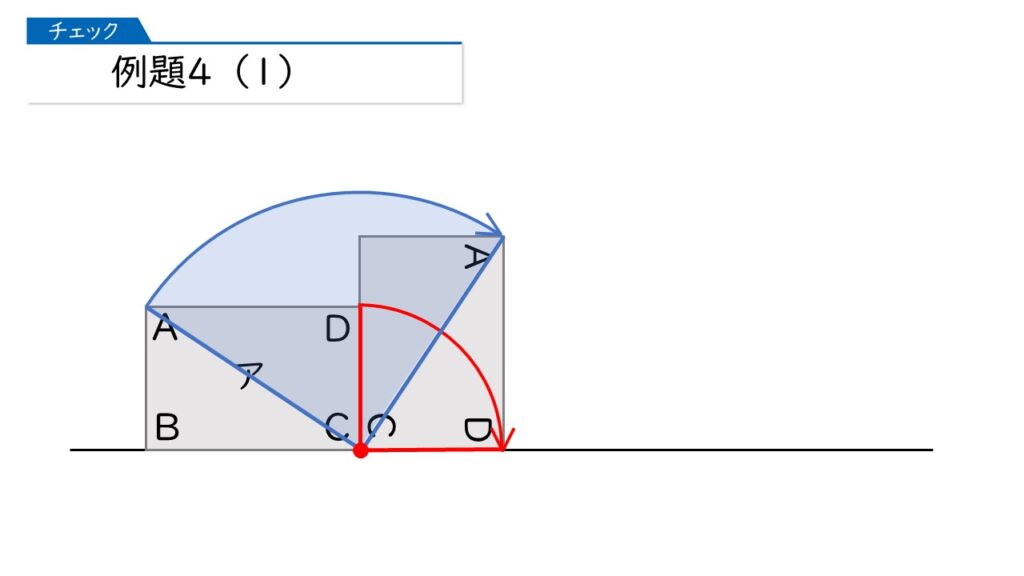
そして、頂点Bは次のように動きます。

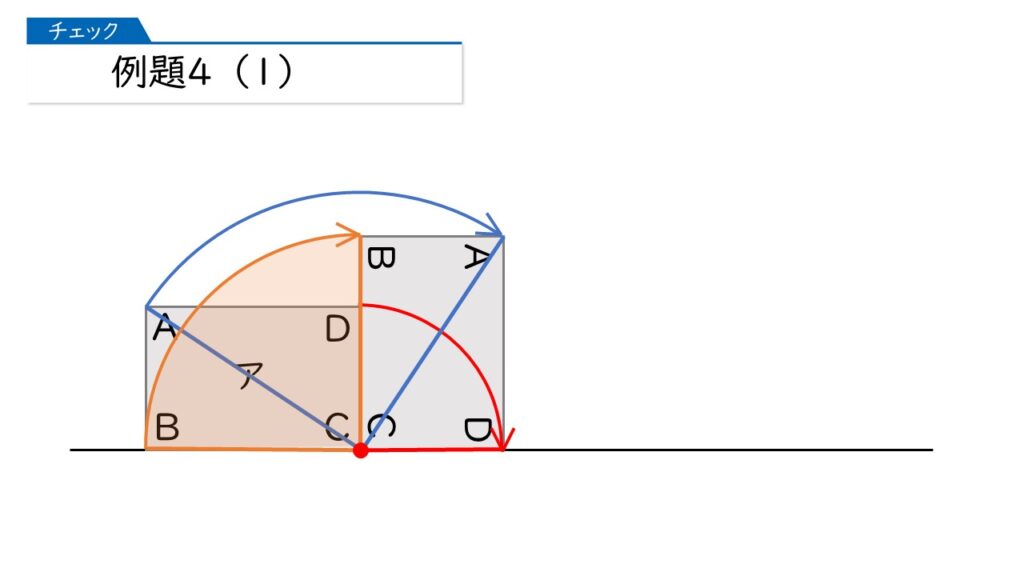
移動した後の頂点を必ず書いてください。この90°の回転移動をあと2回くり返したとき、移動後の各頂点は下の図のようになります。

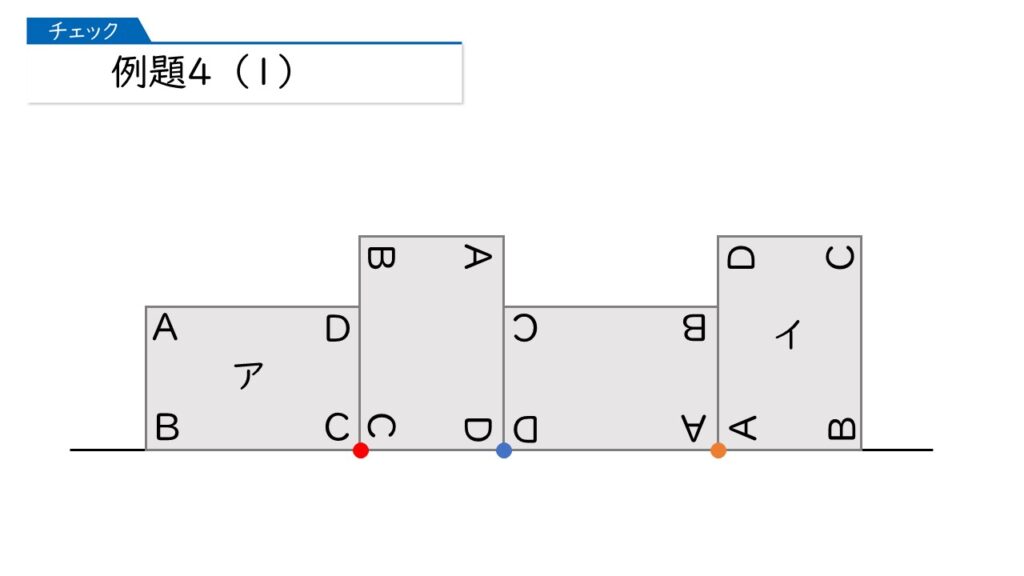
この作業を必ず自力でやっておくことが大事ですよ!

わかったわ!

すると、(1)で「頂点Bが動いたあとの線の長さ」は下の図の弧の長さの和になります。

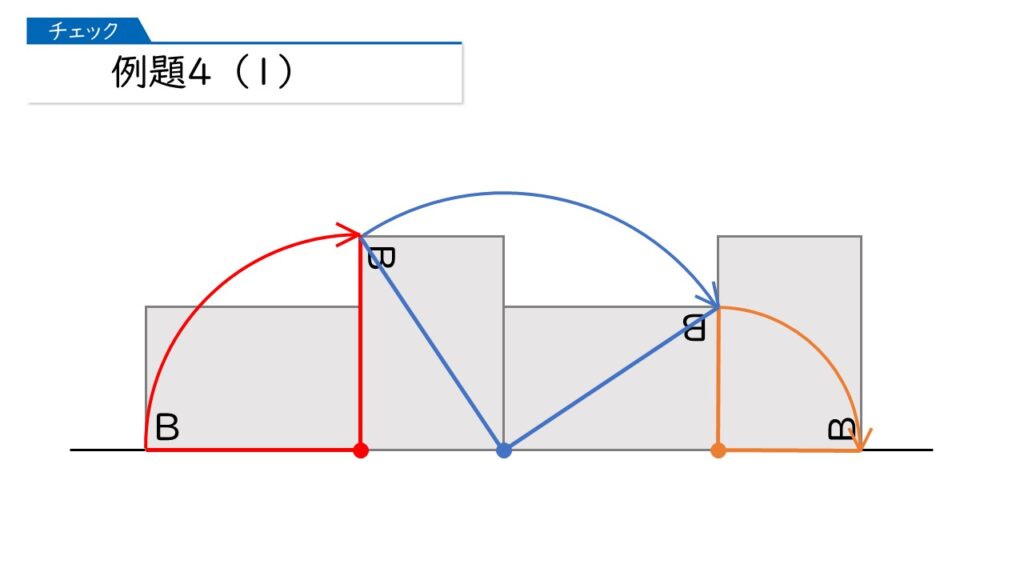
(16+20+12)×3.14×$\dfrac{90}{360}$=37.68(cm)が正解ね!

正解です!

例題4(2)の解き方
すると、(2)で、頂点Bが動いたあとの線と直線ℓで囲まれた図形の面積は、下の図で、3つのおうぎ形の面積と斜線の2つの直角三角形の面積の和になります。

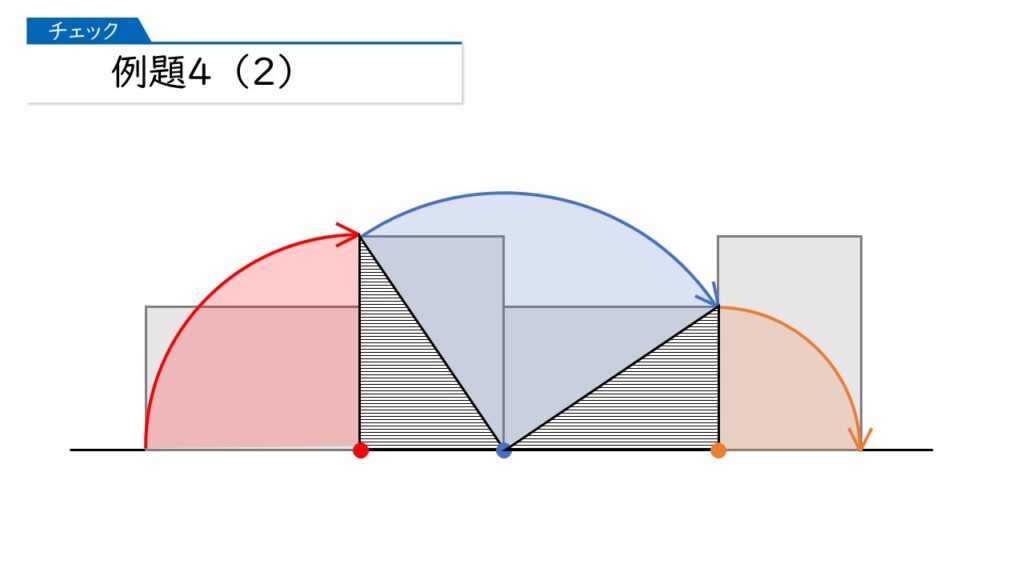
(64+100+36)×3.14×$\dfrac{90}{360}$+8×6=205(cm2)が正解ね!

ご名答です!
これまでやってきたように、図形全体の動きを順序よく追っていくことが大事です。

予習シリーズ算数 多角形の回転・転がり移動 例題5
では最後、例題5をやってしまいましょう。例題5は(1)と(2)がありますが、両方一気に解いちゃいますね。
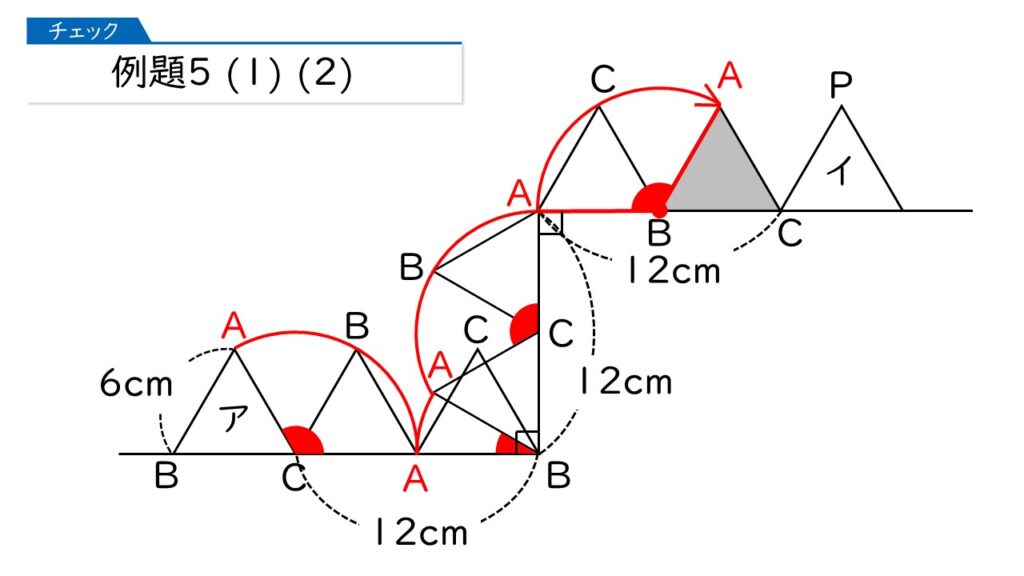
(1)下の図で、正三角形ABCがイの位置にきたとき、Pの位置にくるのは、A、B、Cのどの頂点ですか。
(2)下の図で、頂点Aが動いたあとの線の長さは何cmですか。

第8回-例題5-1024x576.jpg)
ひぇ~、目が回りそうだわ! でも、1回転ずつ、自分の手を使って調べていくことが大切なんですよね。

その通りです! まず、頂点Cを中心に回転させましょう。頂点Aと頂点Bがどのように移動するかに注目です。


頂点Aは、半径6cm、中心角120°のおうぎ形の弧の長さの分だけ動いたわ。

そうですね。さらに、頂点Aを中心として回転しましょう。

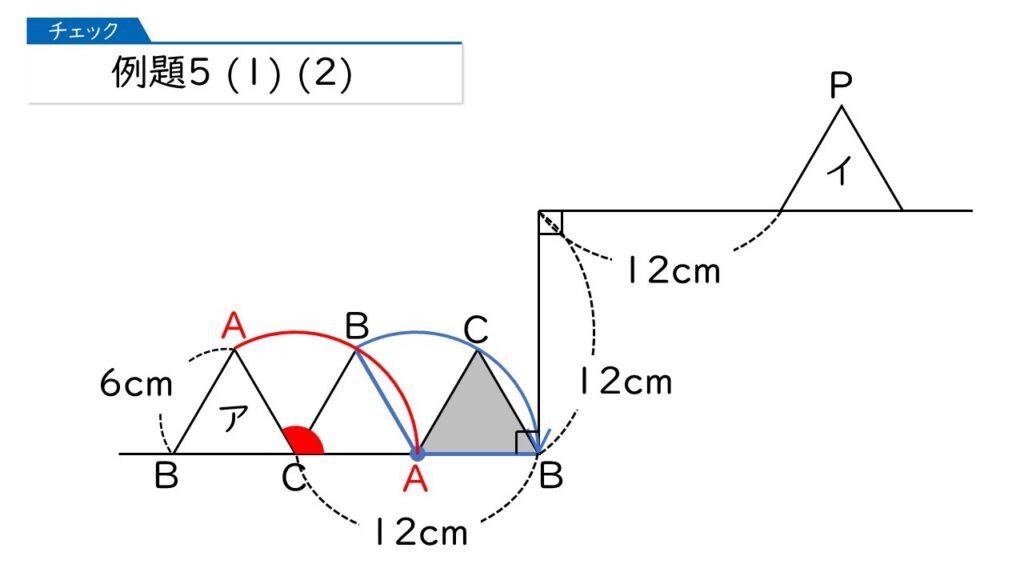
この場合、頂点Aは動かないのね。

そうです。さらに、頂点Bを中心として回転しましょう。

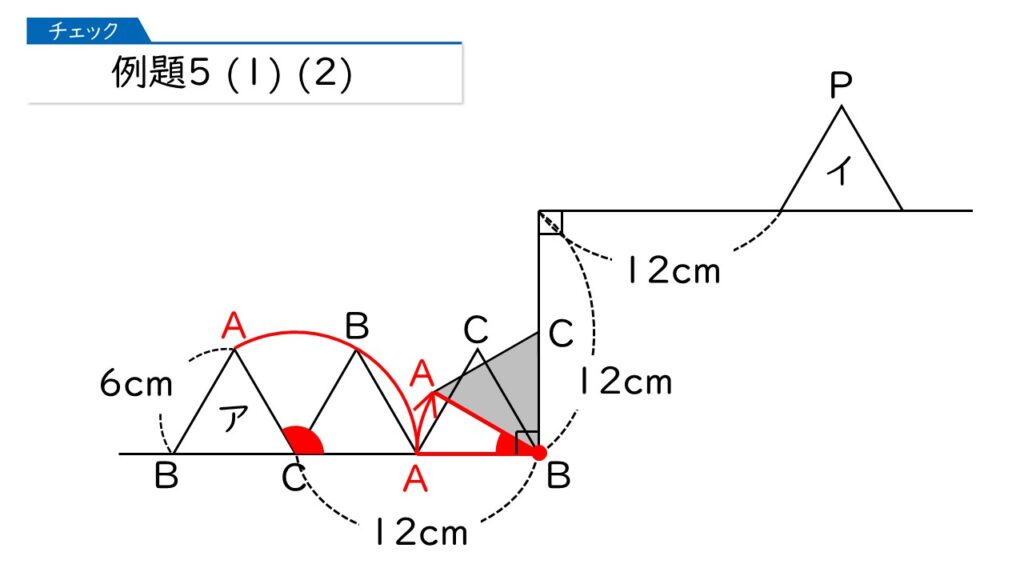
頂点Aは、半径6cm、中心角30°のおうぎ形の弧の長さの分だけ動くのね。

そうです。この問題では、ここの部分に注意が必要ですね。あとはカンタンなので、どんどん回転させていきますね。



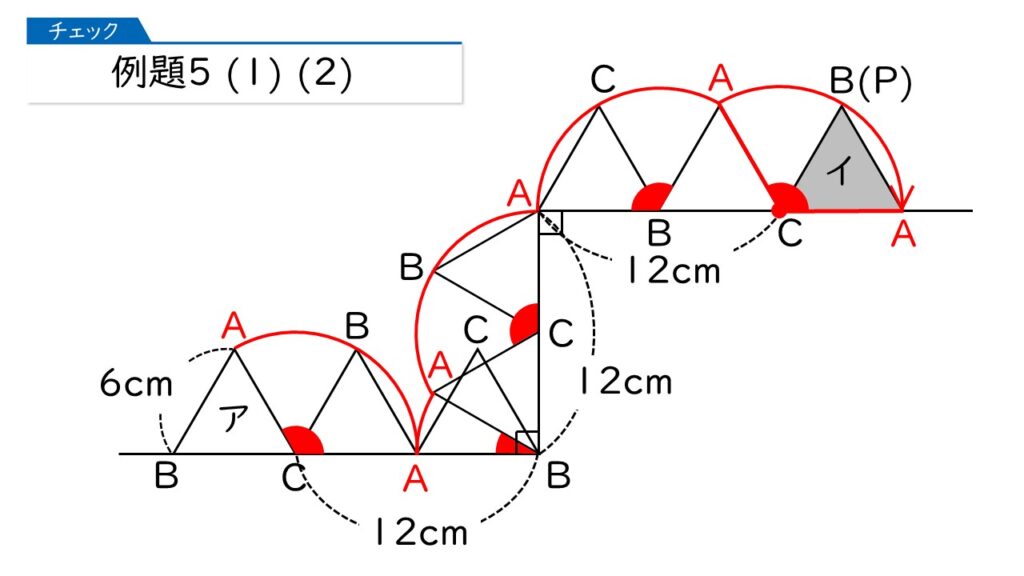
(1)で、Pの位置にくるのは頂点Bってわかったわ。
(2)で、頂点Aが動いたあとの線の長さは、赤いおうぎ形の弧の長さを足せばいいのね。

その通りです! (2)は次のように計算して、計算ミスを減らしましょう。
6×2×$\dfrac{120×4+30}{360}$×3.14=53.38(cm3)

さらに応用問題に挑戦!
今回の例題は基本レベルだけでしたので、さらに難しい応用問題に挑戦したい人はチャレンジしてください。
YouTube「クイックラーニング 中学受験算数教室」から出題です。まず、プリントをダウンロードしてください。解いてから、動画で解説を聞いてくださいね。
多角形の回転_応用問題 (1293 ダウンロード )
今日もお疲れさまでした。予習シリーズでは、多角形を回転させた後の完成図しか書いてありませんが、この図を元にして計算しても、できるようになったことにはなりません。
しつこいようですが、必ず自分の手で、回転運動の最初から最後までを書くようにしてください。

わかったわ。めんどうだけど、それが一番身につくということね。

はい! どうもうまく書けないときは、下のフォームから質問してくださいね。








