四谷大塚 予習シリーズ 算数 徹底解説 5年上第11回 場合の数－ならべ方－クイックラーニング
yamada
中学受験マスターガイド
四谷大塚 予習シリーズ 算数 徹底解説 5年上第12回 場合の数－組み合わせ方－クイックラーニング
yamada
記事内に商品プロモーションを含む場合があります
予習シリーズ5年前期で「場合の数」を学びます。「場合の数」のうち、前回の11回では「ならべ方」をやりました。今回、12回では「組み合わせ方」をやりますね。
前回は樹形図を使っていろいろな問題を解いたわ。今回は、前回とどうちがうの？
さすがです、いい質問ですね！
前回の「ならべ方（順列）」では、ならべる順序を問題にして考えますが、今回やる「組合せ」では順序を問題にしないで取り出し方だけを問題にして考えます。
ど、どういうこと？
例えば、クラス全員の中から、太郎くんと次郎くんがリレーの選手に選ばれたとき、さらにどちらが先に走るかを決めなければいけませんね。この場合、「選んでならべる」という意味で「ならべ方（順列）」と言います。
そうすると、「ならべ方」では、太郎くん→次郎くん、次郎くん→太郎くん、の2通りとなります。これが前回やったものです。
これに対して、クラス全員の中から、太郎くんと次郎くんが掃除当番に選ばれたとき、そのあとどちらが先とか後とか考えなくていいですよね。この場合、「選ぶだけでならべない(順番を区別しない)」という意味で「組み合わせ」と言います。
そうすると、「組み合わせ」では、太郎くんと次郎くん、の1通りとなります。これが今回やるものです。
なるほど、前回と今回のちがいは「ならべるかどうか」で、今回の「組み合わせ」は、ならべるない数え方、というわけね。
そうです！ では、さっそく例題をみていきましょう！
この記事の目次
予習シリーズ算数 場合の数(ならべ方) 例題1
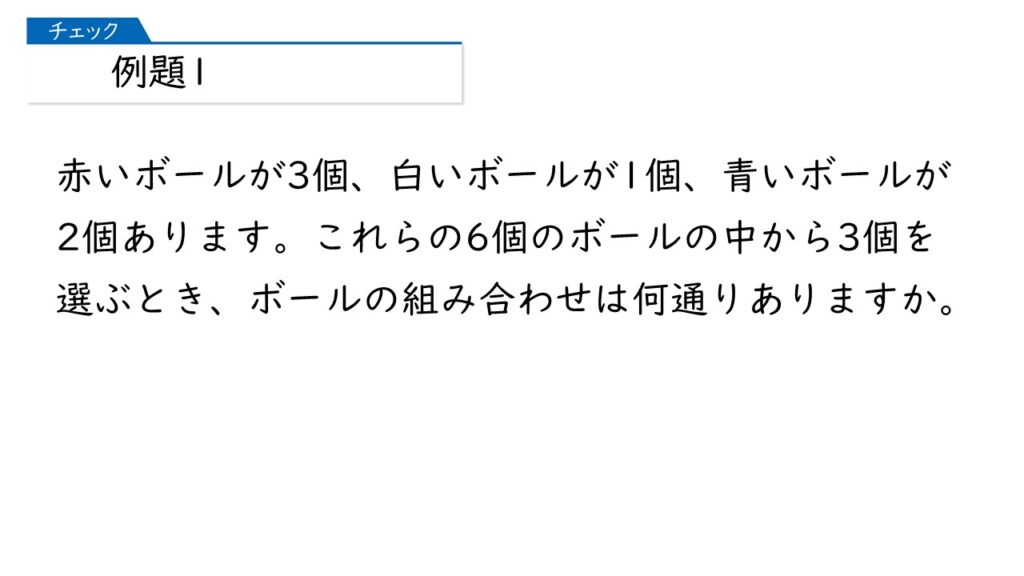
この問題は、（赤、白、青）とかの組み合わせを考えればいいのね。
でも、（赤、白、青）と（赤、青、白）は同じだから、混乱しちゃうわ。
そうですよね。でも「すべての場合」を見渡すことができれば、自信をもって答えられますよ。
この問題の場合は、赤いボールを基準に場合分けをしましょう。
赤いボールを基準に場合分けをするって、どういうこと？
すべての組み合わせは、赤が3個、赤が2個、赤が1個、赤が0個のどれかになる、ということです。
まず、赤が3つの場合は何通りありますか？
赤が3個あるから、1通りね。
その通りです！
では、赤が2個ふくまれる場合は何通りですか。
赤2個と白1個、赤2個と青1個で、2通りね。
おっ、即答ですね！ では、赤が1個ふくまれる場合は何通りですか？
青が2個あることに注意ね！
赤1個と白1個と青1個、それと、赤1個、青1個、青1個。これで2通りだわ。
すばらしいです！ では最後。赤が1つもふくまれない場合は何通りですか？
白1個、青1個、青1個の1通り！
そうすると、全部で6通りになるってことね。全体像が分かって、数え方にもれがないから、自信をもって答えられるわ。
そうです！
では、例題2に進みましょう。ここからが本番です。
予習シリーズ算数 場合の数(ならべ方) 例題2
「リレー型」と「そうじ当番型」のちがい
まず、「リレー型」と「そうじ当番型」のそれぞれの数え方をみてみましょう。
A, B, C, D の4人から，3人の「リレー選手」を選ぶ方法は何通りありますか。
樹形図をイメージすればいいのね。4×3×2＝24通りあるわ。
そうです、その通りです！
A, B, C, D の4人から，3人の「そうじ当番」を選ぶ方法は何通りありますか。
そうじ当番の場合は、リレー選手のときとちがって、(ABC)(ACB)(BAC)(BCA)(CAB)(CBA) はまとめて1通りと考えますよ。
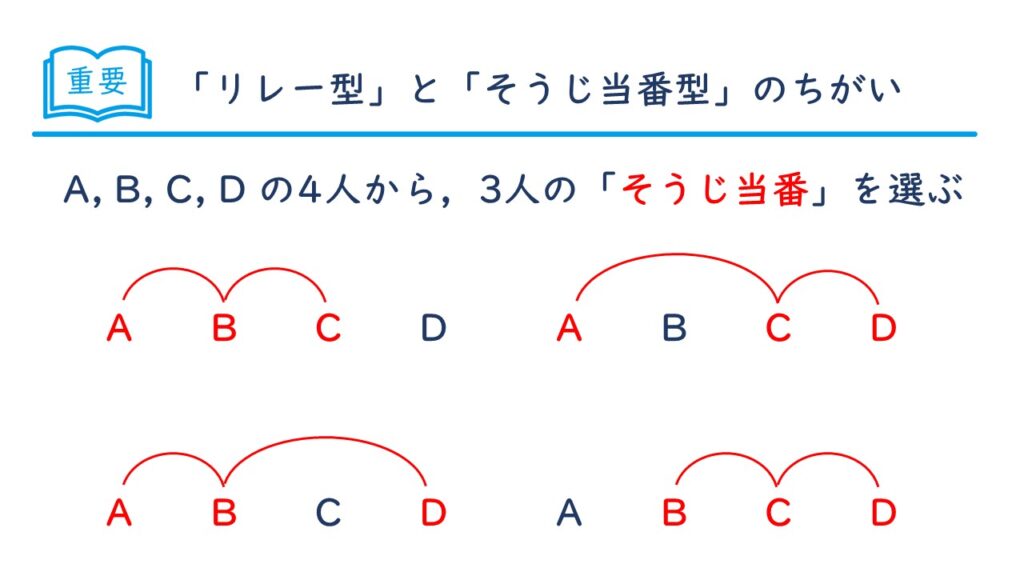
そうすると、上の図のように、(ABC)(ACD)(ABD)(BCD)の4通りになります。
この方法だと、数えもれがでそうで、心配だわ…
そうですよね。
「そうじ当番型」の場合も、「リレー型」の計算を利用して、カンタンに求めることができます。
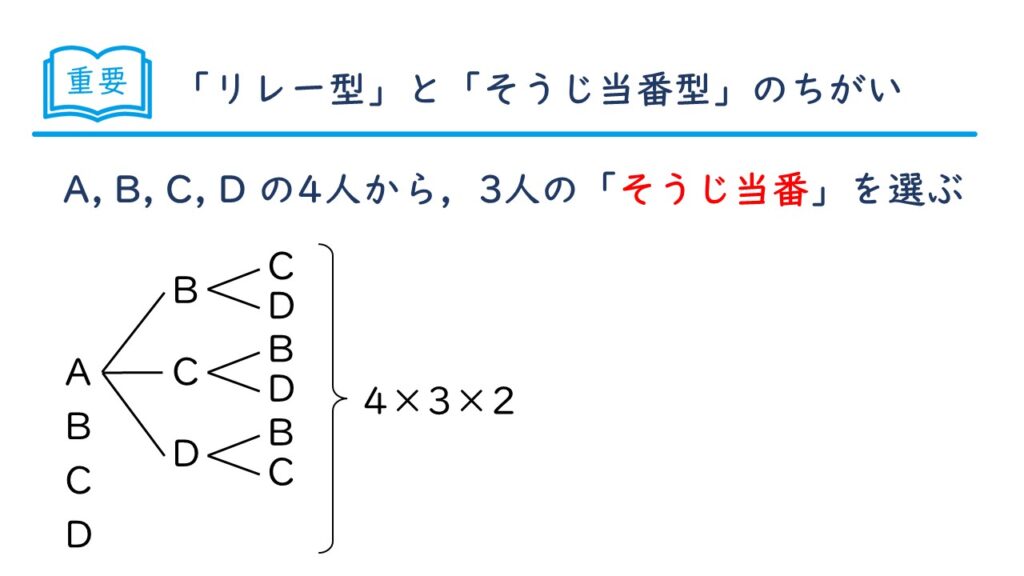
「リレー型」で使った上の樹形図の中には、例えば、(ABC)の組み合わせが、(ABC)(ACB)(BAC)(BCA)(CAB)(CBA)の6通りがダブって入っています。
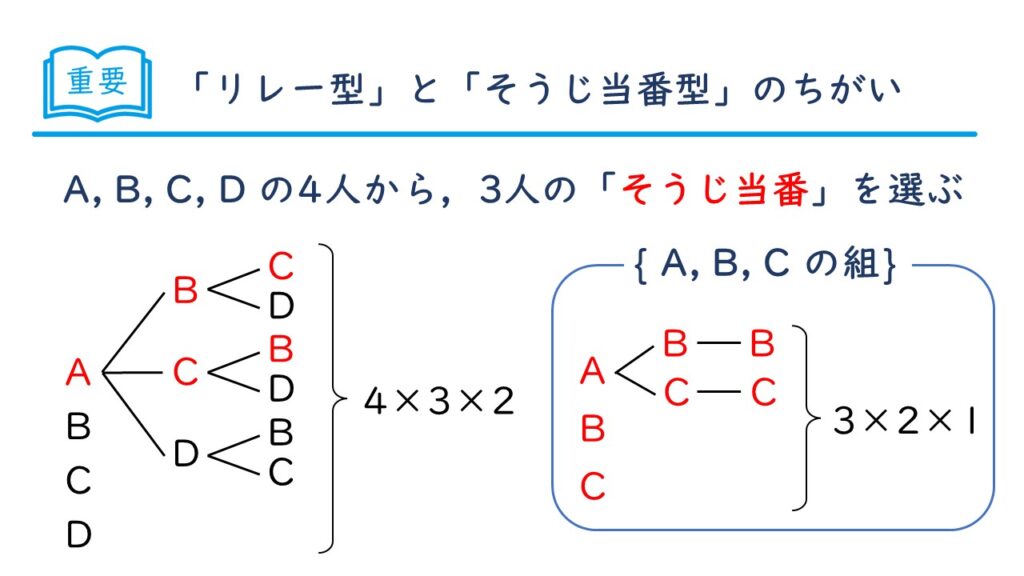
(ABC)の組み合わせだけでなく、(ACD)(ABD)(BCD)のそれぞれの組み合わせでも6通りずつダブっています。
つまり、(ABC)×6＋(ACD)×6＋(ABD)×6＋(BCD)×6＝4×3×2 ということがわかります。
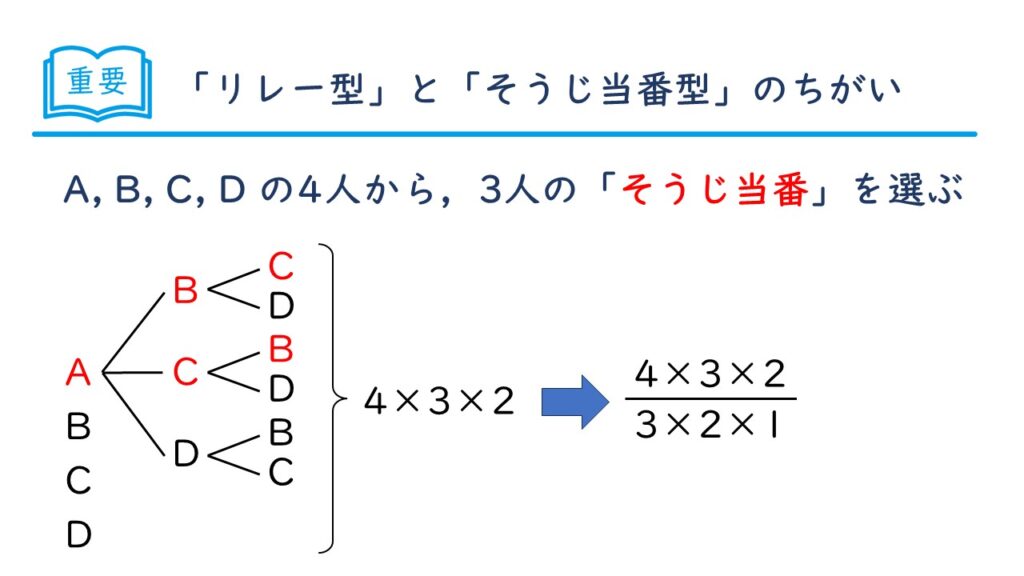
すると、「4人から3人のそうじ当番を選ぶ方法」は、上の式で求めることができるんです。
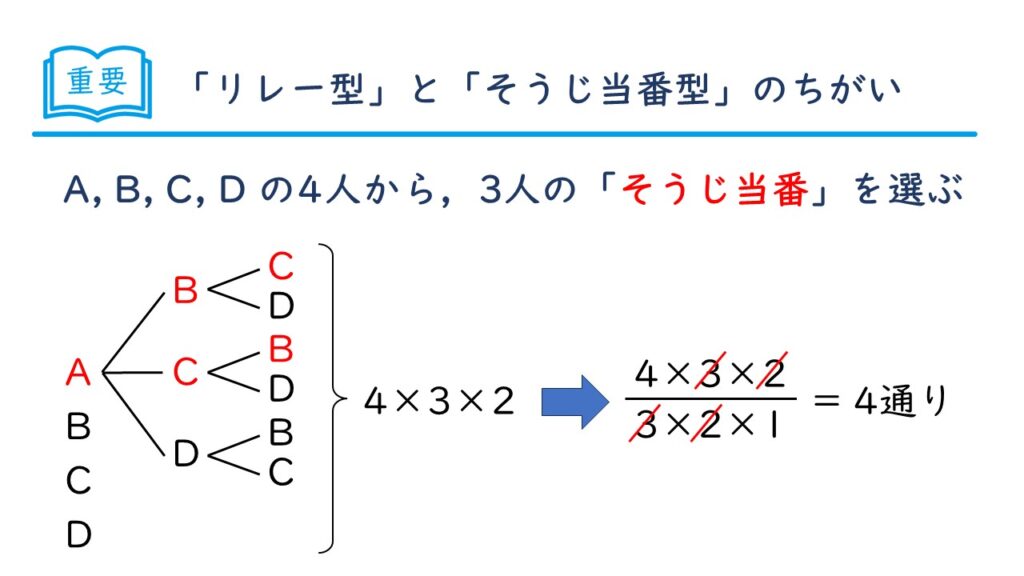
本当だわ！ 約分して計算すると、確かに4通りね。
はい。一度慣れてしまえば、スッと使えるようになりますので、ここで練習しておきましょう！
「そうじ当番型」の計算練習
まず、「3人中1人」を選ぶ方法は1通りですね。
次に、「3人中2人」を選ぶ方法は3通りです。
なぜかというと、「そうじ当番に選ばれない1人の選び方」(3人中1人)と同じだからです。
次に、「4人中1人」の選び方は4通りですね。
次に、「4人中2人」の選び方は何通りありますか？
ここは計算でサクッと出しましょう！
「〇人中2人」ときたら、樹形図で考えることができるすべての場合（リレー型）を、（2×1）で割ればいいんですね。
じゃぁ、「4人中3人」の選び方は何通りありますか？
「〇人中3人」ときたら、樹形図で考えることができるすべての場合（リレー型）を、（3×2×1）で割ればいいんですね。
ただこの場合、「そうじ当番に選ばれない1人の選び方」(4人中1人)と同じだから、計算しなくてもでますね。
では、さらに人数を増やしていきましょう！
「5人中1人」の選び方は5通りですね。
では、「5人中2人」の選び方は何通りありますか？
「〇人中2人」だから、樹形図で考えることができるすべての場合（リレー型）を、（2×1）で割るんでしょ！
お～、よくできましたね！
じゃぁ、「5人中3人」の選び方は何通りありますか？
もう、かんたんだわ。「〇人中3人」とあるから、樹形図で考えることができるすべての場合（リレー型）を、（3×2×1）で割るんでしょ。
さすがです！
じゃぁ、「5人中4人」の選び方は何通りありますか？
「〇人中4人」とあるから、樹形図で考えることができるすべての場合（リレー型）を、（4×3×2×1）で割るんでしょ。
よく気づきましたね！
最後の計算は、「そうじ当番に選ばれない1人の選び方」(5人中1人)と同じだと考えてもいいですね。
では、これを使って、例題2を解いていきましょう！
例題2（1）の解き方
問題では「日直」とありますが、(AB)と(BA)を区別せず合わせて1通りと考えますから、「そうじ当番」と同じですね。
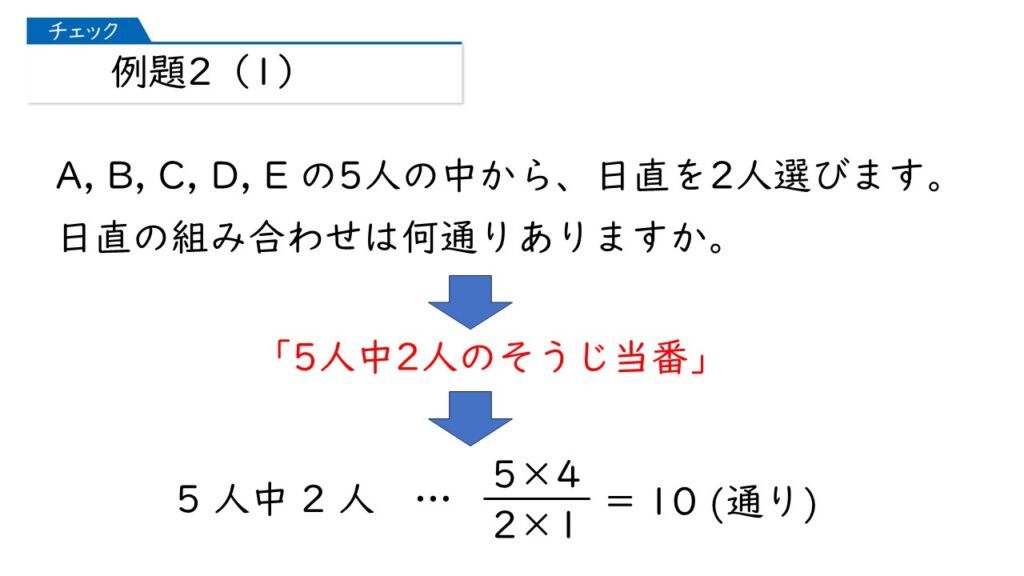
つまり、「5人中2人」のそうじ当番の選び方ということね。
その通りです！
そうすると、さっきやった計算練習の方法で、カンタンに答えが出るわ。
例題2（2）の解き方
これはもう、かんたんだわ。「7人中3人」のそうじ当番の選び方ということね。
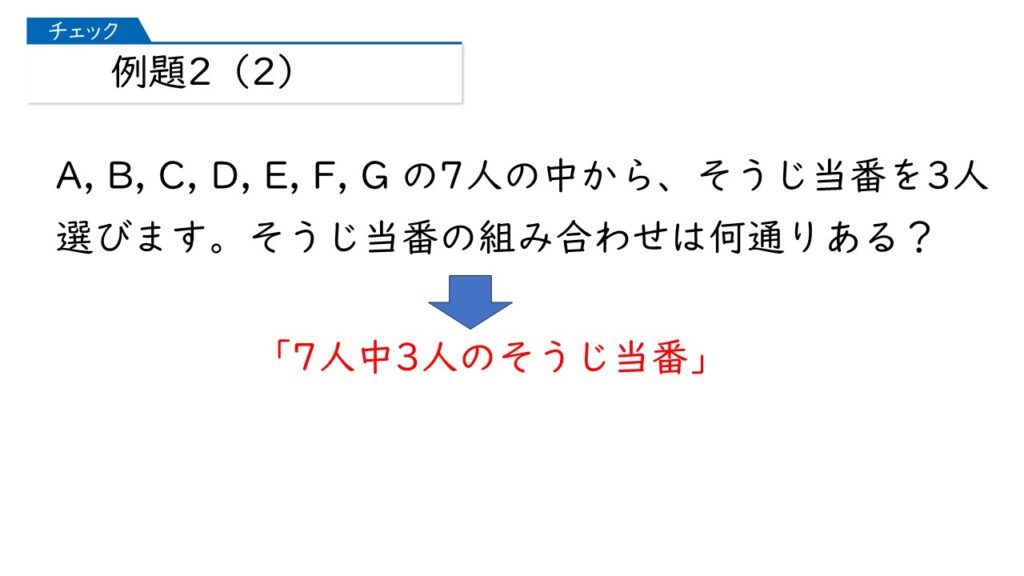
「〇人中3人」とあるから、樹形図で考えることができるすべての場合（リレー型）を、（3×2×1）で割れば答えだわ。
ご名答です！ 私の出番がなかったですね…
予習シリーズ算数 場合の数(ならべ方) 例題3
例題3（1）の解き方
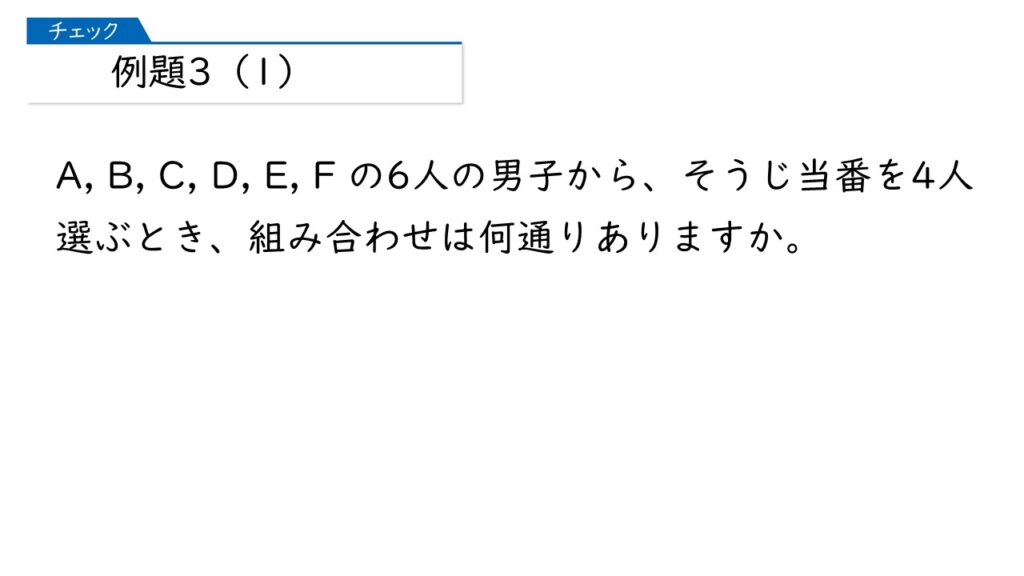
「6人中4人」のそうじ当番の選び方ね。
「6人中4人」のそうじ当番の選び方ね。
「〇人中4人」とあるから、樹形図で考えることができるすべての場合（リレー型）を、（4×3×2×1）で割れば、答えがすぐ出るわ。
また、私の出番がなかった…
例題3（2）の解き方
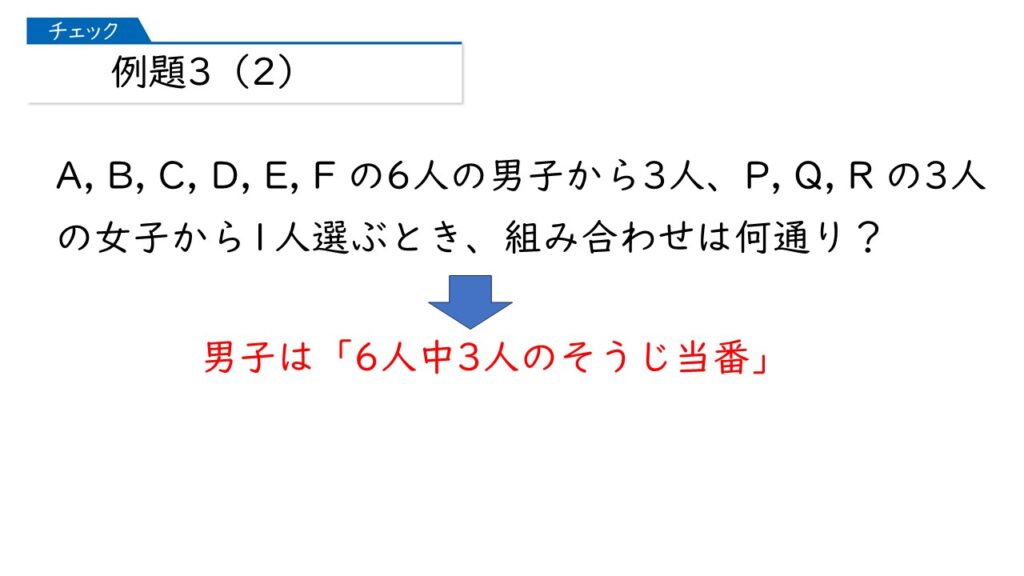
この問題は、まず、男子の選び方を求めましょう。
男子だけみれば、「6人中3人のそうじ当番」の選び方ね。
その通りです！
次に、男子のこの20通りのそれぞれについて、女子の選び方が何通りあるかを考えます。
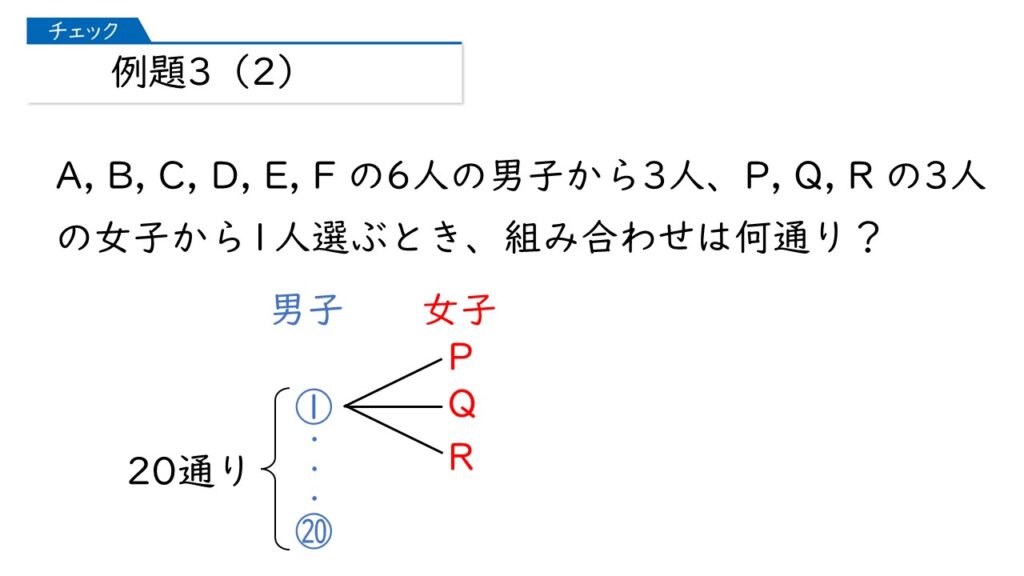
なるほど！ 男子の選び方は20通りあって、それぞれについて、女子の選び方が3通りあるから、20×3＝60通りが答えね。
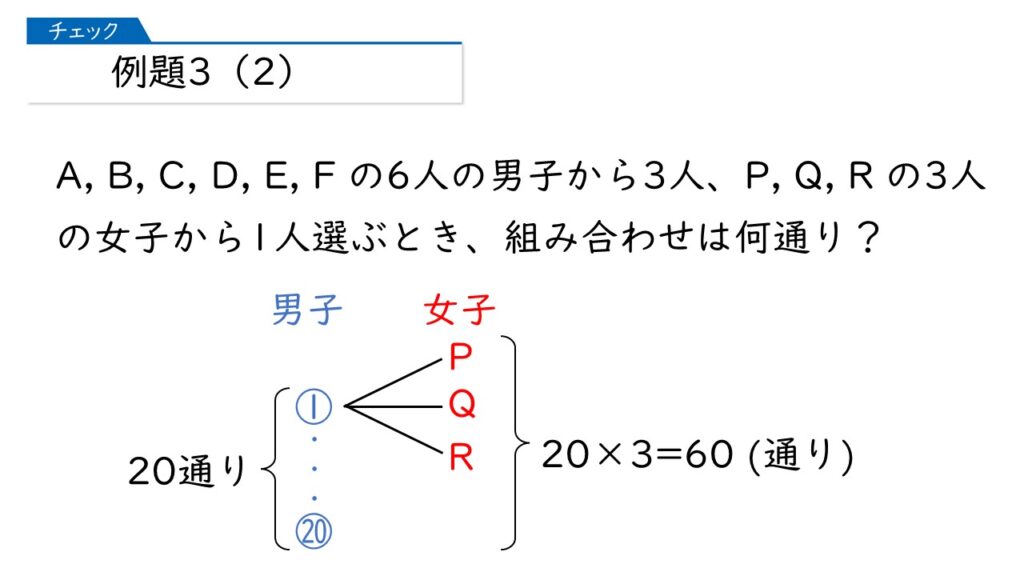
よくできました！
もし、女子の選び方が3人中2人になっても、女子の選び方は3通りになりますから、答えは同じになりますよ。
予習シリーズ算数 場合の数(ならべ方) 例題4
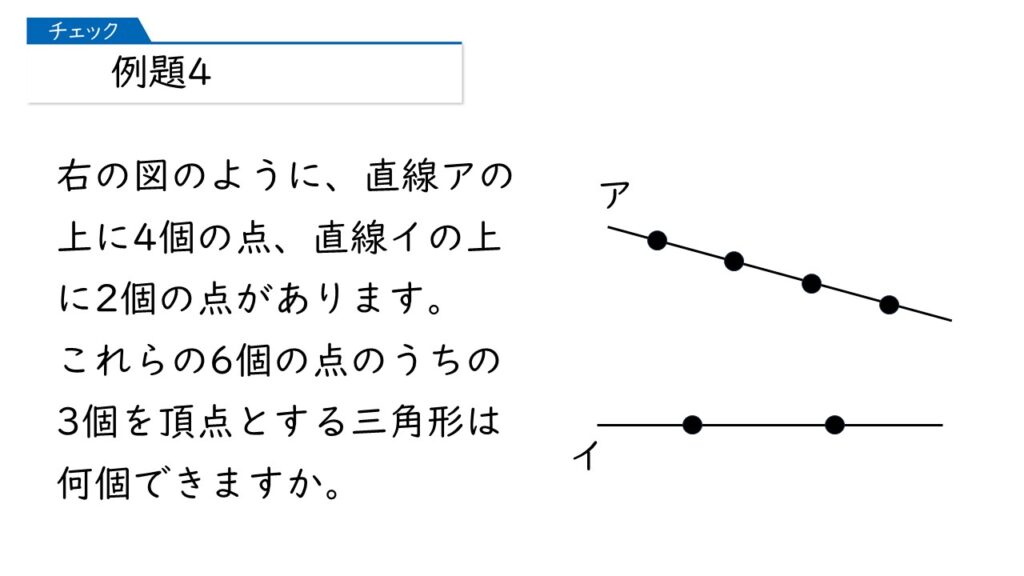
三角形の形が具体的にイメージできるように、底辺と頂点とで場合分けをして考えますね。
まず、アが頂点、イを底辺としたとき、三角形はいくつできますか。
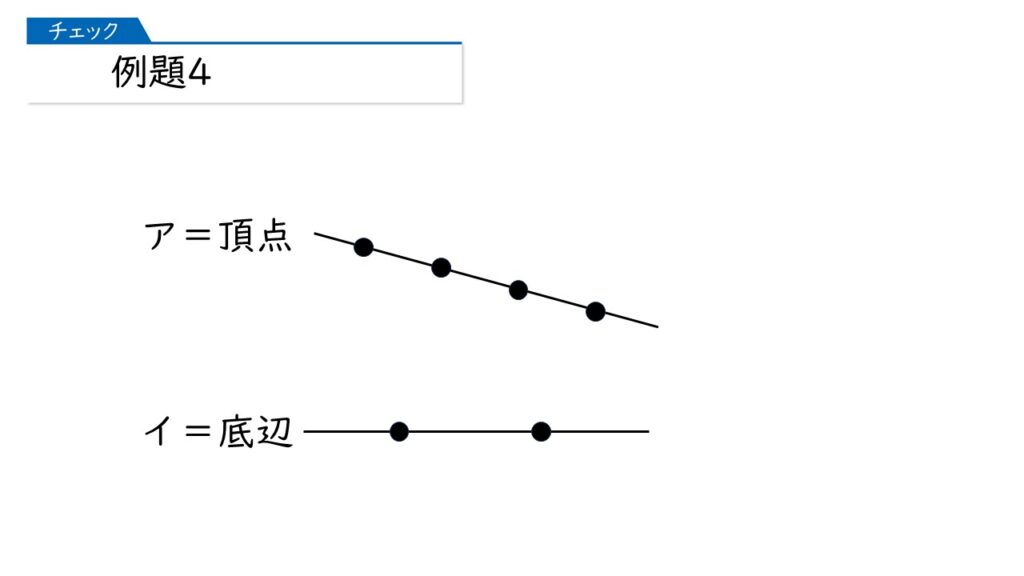
頂点が4つできるから、4通りね！
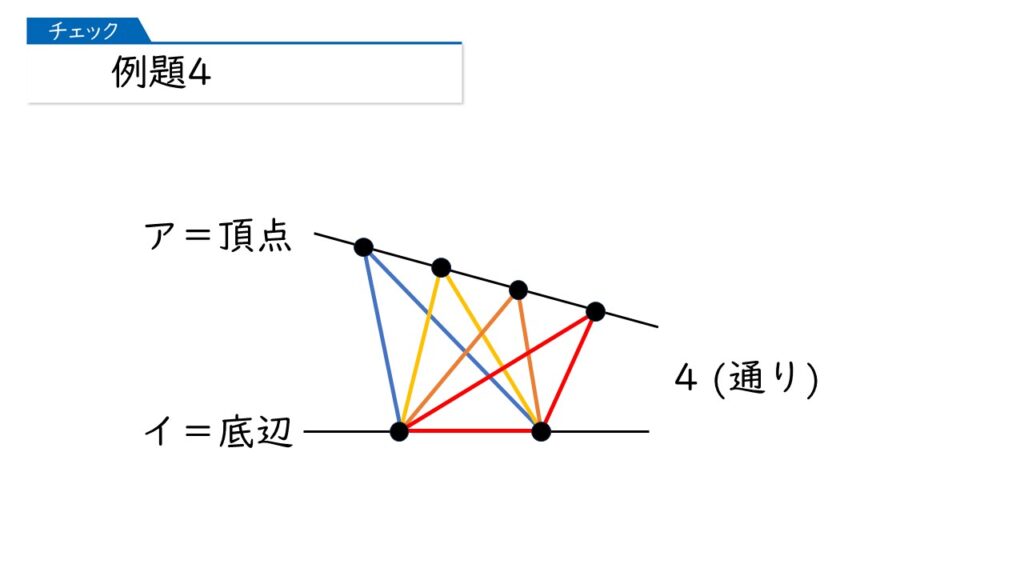
その通りです！
では次に、アが底辺、イを頂点としたとき、三角形はいくつできますか？
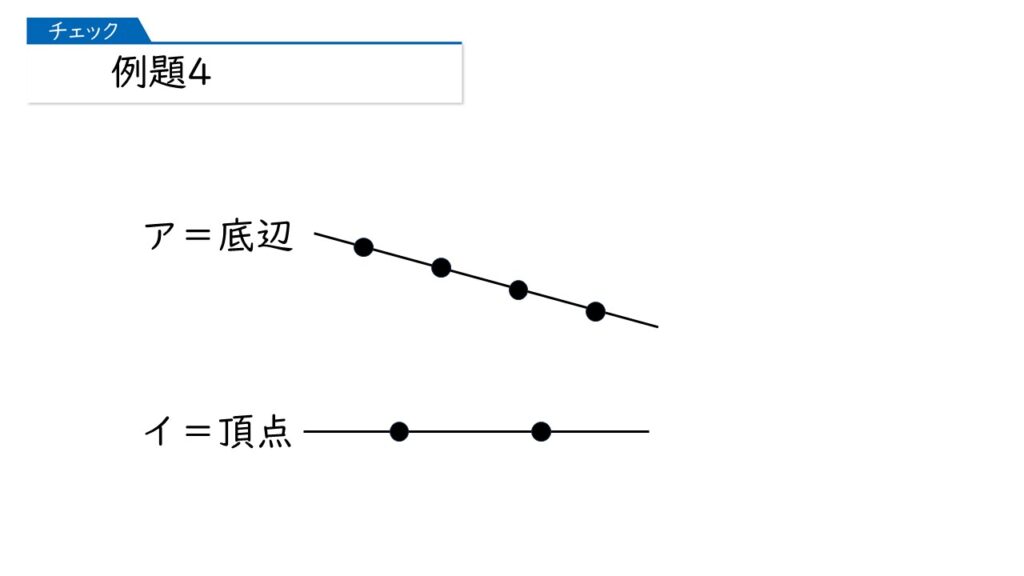
底辺は、4つの点のうち2つの点を選べばいいですね。
そうすると、下の図のように、底辺の選び方は6通りになります。
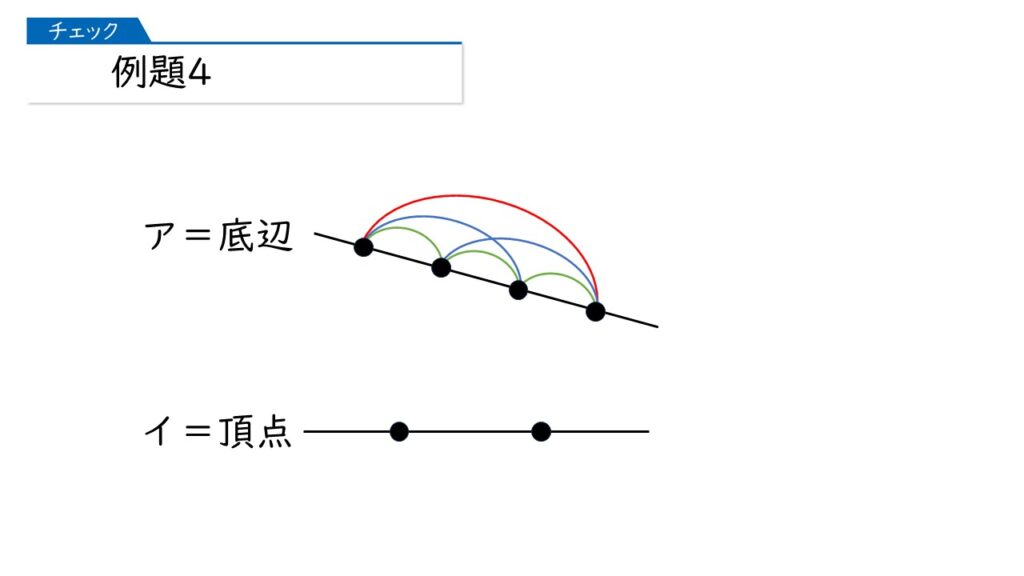
「4点中2点」を選べばいいから、$\dfrac{4×3}{2×1}$ で計算すればいいんじゃないかしら？
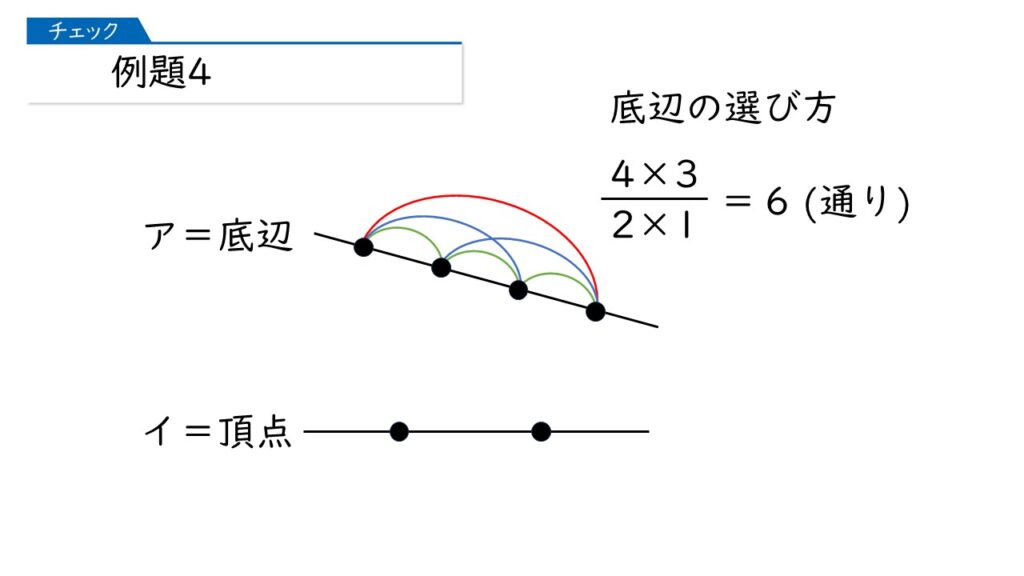
おっ、するどい。そうした方がよかったです！
そうすると、アが底辺、イを頂点としたとき、三角形はいくつできますか？
底辺の選び方が6通りあって、それぞれについて、頂点の選び方が2通りあるから、6×2＝12通りね。
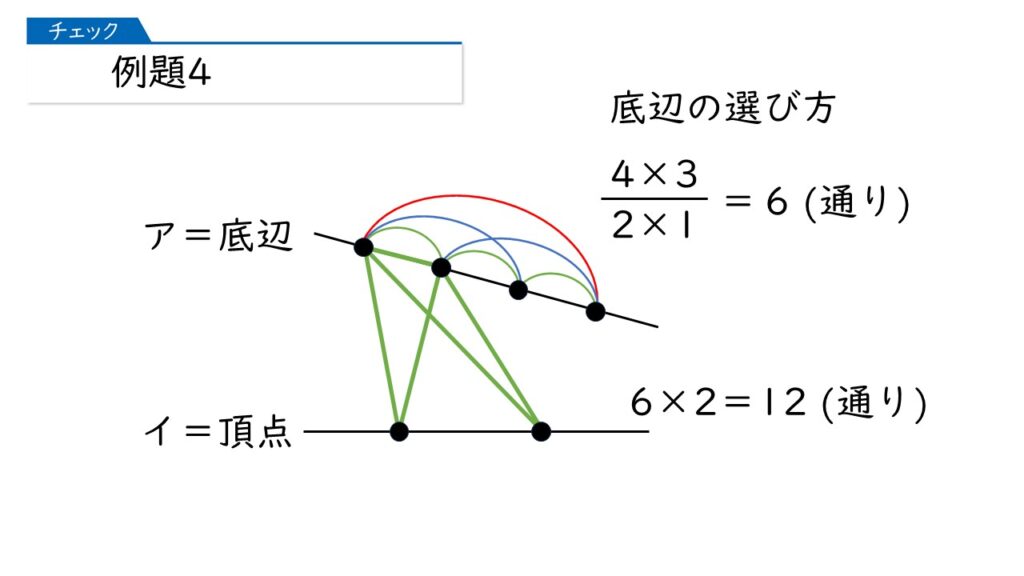
はい、その通りです。そうすると、4通りと12通りをたして、答えは16になります。
予習シリーズ算数 場合の数(ならべ方) 例題5
この問題では、下のような前提となる重要なポイントがありますので、まず、これを覚えてくださいね。
そうすると、この問題では、{ 0⃣, 1⃣, 2⃣, 3⃣, 4⃣ }の中から3枚のカードを選ぶとき、その3枚に書かれた数の和が3の倍数でなければならないわけです。
では、3つの数の和が3の倍数になるような組み合わせを調べてみましょう。
次のようにして考えると、上手に選ぶことができますよ。
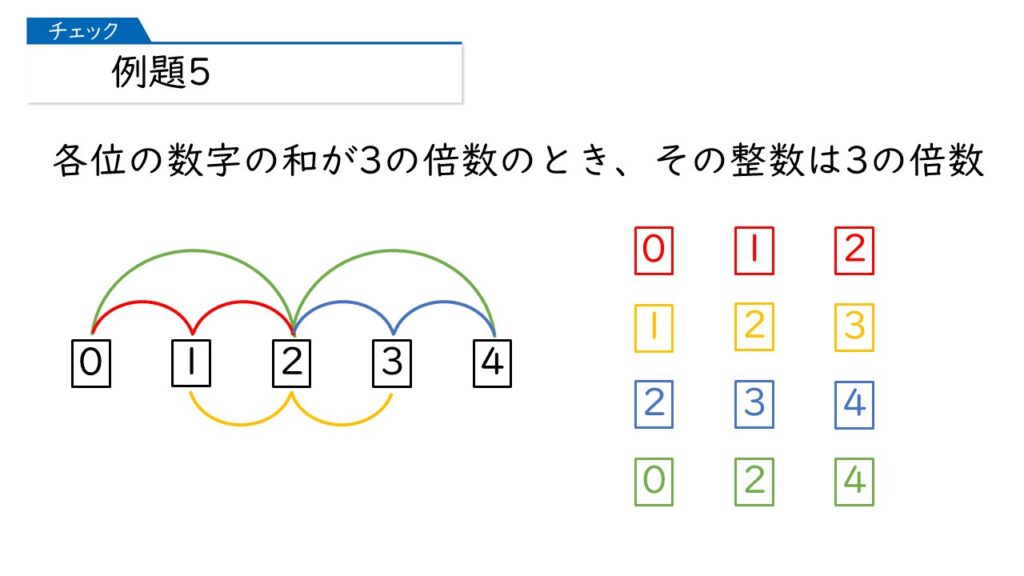
なるほど！ 連続する数の場合、「となり合う3つの数」か、「1つおきの数」の和は3の倍数になるのね。
その通りです！
さらに、この問題は「3けたの整数は何通りか」とありますから、「リレー型」です。
なので、(0,1,2)(1,2,3)(2,3,4)(0,2,4)のそれぞれについて、何通りずつあるかを調べましょう。
3けたの整数だから、それぞれ(3×2×1)通りずつあるから、全部で(3×2×1)×4＝24通りになるわ。
惜しいです。その考え方だと、百の位に「0」がくることになって、その場合は2けたになってしまいます。
だから、「0」をふくむ組合わせと、「0」をふくまない組み合わせを別々に調べないといけません。
そうすると、「0」をふくむ組合わせの場合の樹形図と、「0」をふくまない組み合わせの場合の樹形図を考えれば、答えが出ますね。
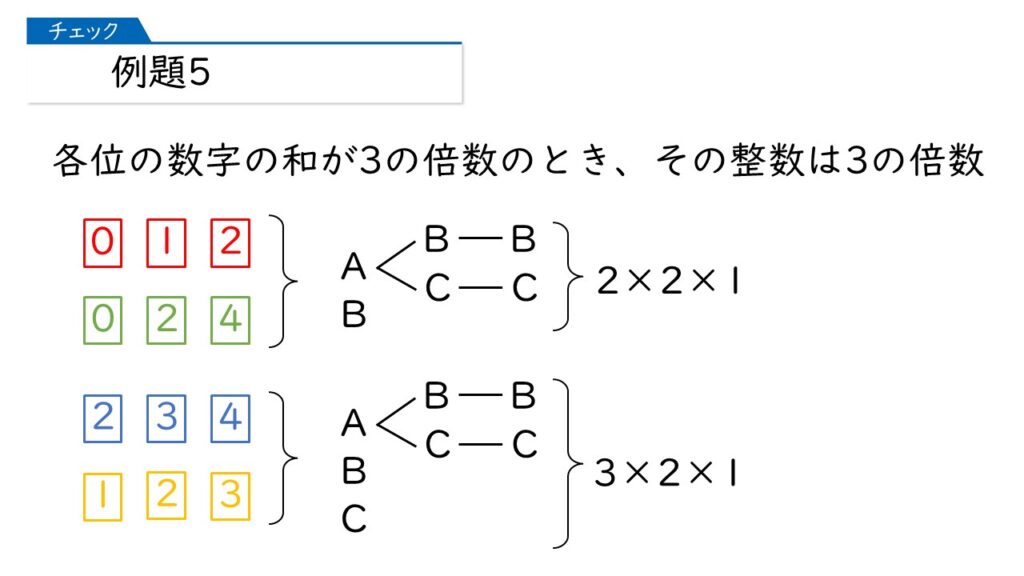
「0」をふくむ組合わせの場合は百の位が2通りで、「0」をふくまない組合わせの場合は百の位が3通りというわけね。
そうすると、(2×2×1)×2＋(3×2×1)×2＝20通り、が正解ね！
よくできました！ 「×2」を忘れなかったのは立派です。
予習シリーズ算数 場合の数(ならべ方) 例題6
例題6（1）の解き方
この問題ですけど、初めて解くときには、全体像を頭の中でイメージできるように、調べ上げていきましょう！
まずは、左はしに1つある場合からです。
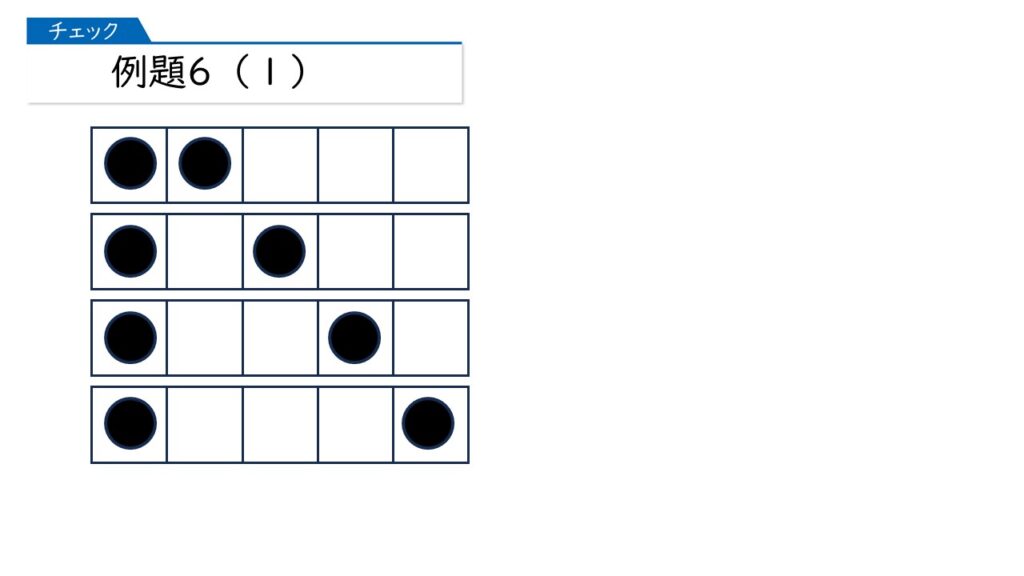
次に、左から2番目に1つある場合です。さっき調べたものの中にだぶっているものがありますから、それを除きます。
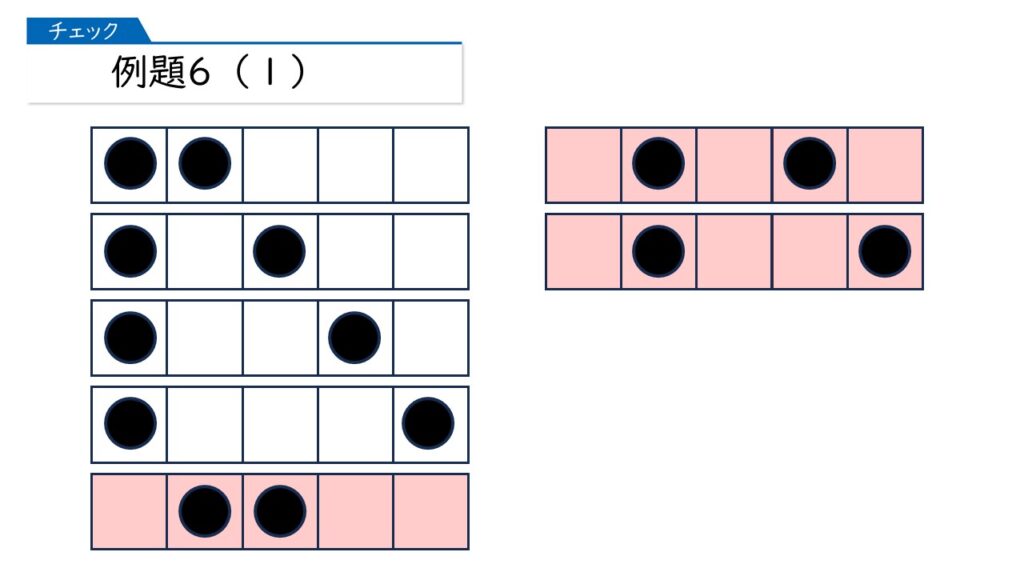
次に、左から3番目に1つある場合です。これまで調べた中にだぶりがありますから、それらは除きます。
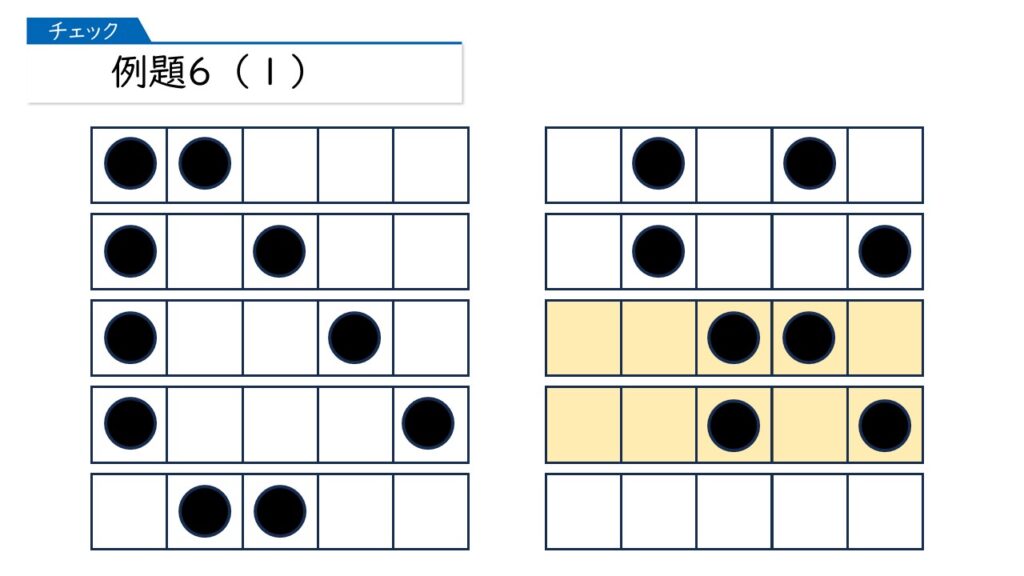
次に、左から4番目に1つある場合です。これまで調べた中にだぶりがありますから、それらは除きます。
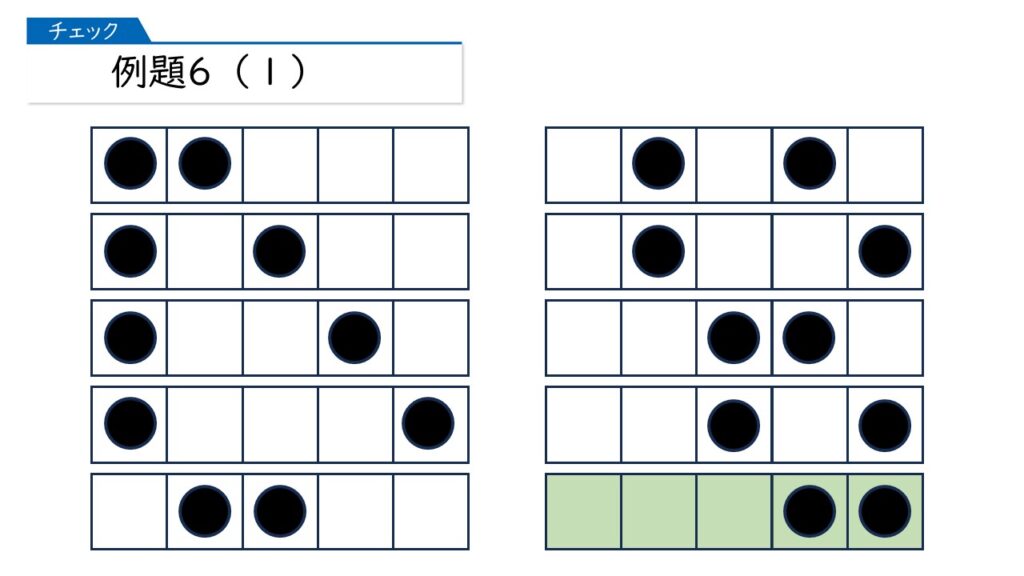
このほかに、並べ方はありますか？
もうないわ。
そうですね。ということで、下の10通りが正解になります。
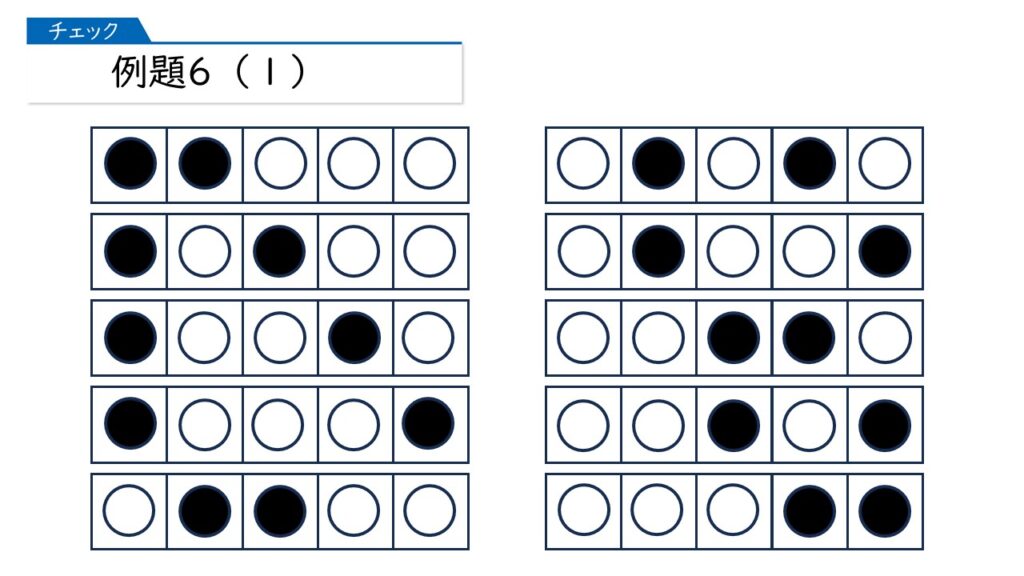
このことから、この問題は「そうじ当番型」の問題だとわかります。
つまり、「5つの席のうち2つを選ぶ」ということです。
なるほど。「5つの席のうち3つを空席にする」と考えても同じ答えになりますね！
するどいですね。その通りです！
この考え方を使えば、(2)もカンタンに解くことができます。
例題6（2）の解き方
この場合、青玉が1つだけなので、青玉の置き方をまず決めます。
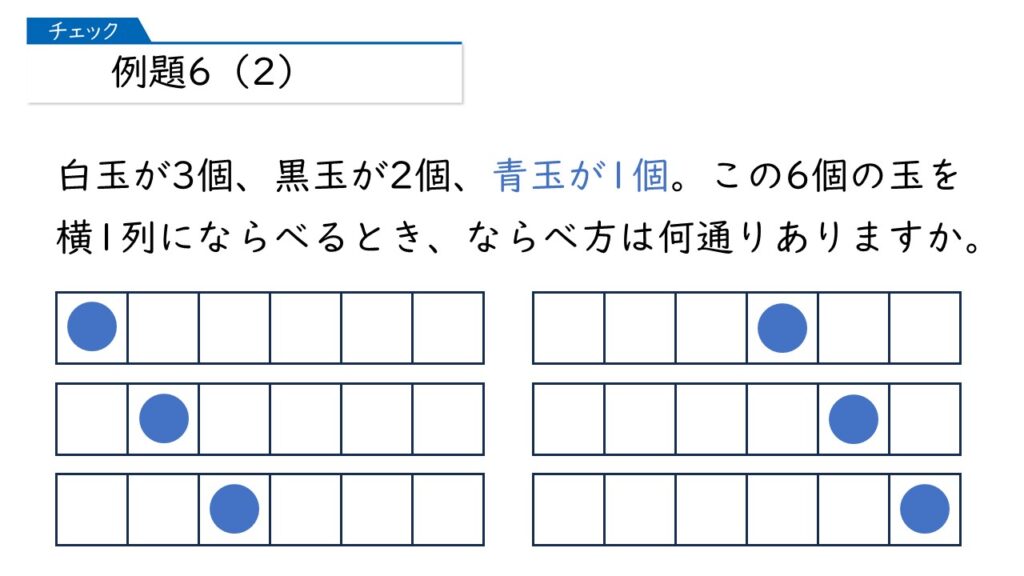
青玉の置き方は6通りあるってことね。あとは、それぞれ、白玉と黒玉の置き方を調べればいいと…
その通りです！もう答えは出ていませんか？
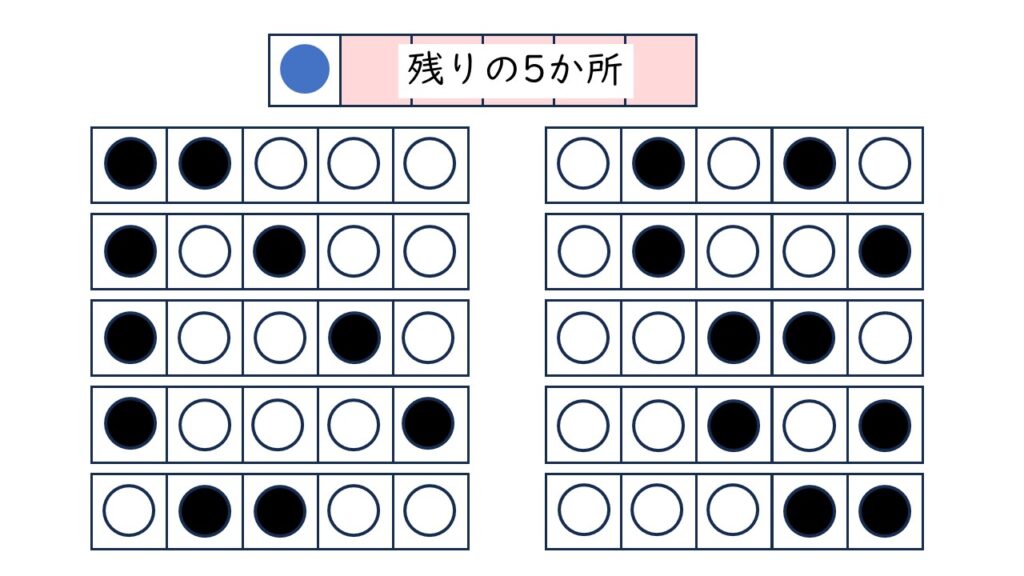
青玉を一番左に置くとき、残りの5か所に白玉と黒玉の置き方は、（1）で求めた10通りになるわ。
なるほど、そうすると、青玉の置き方が6通りだから、答えは6×10＝60通りということね。
その通りです！
予習シリーズ算数 場合の数(ならべ方) 例題7
例題7（1）の解き方
この問題は、解き方を覚えていればカンタンに解けます。
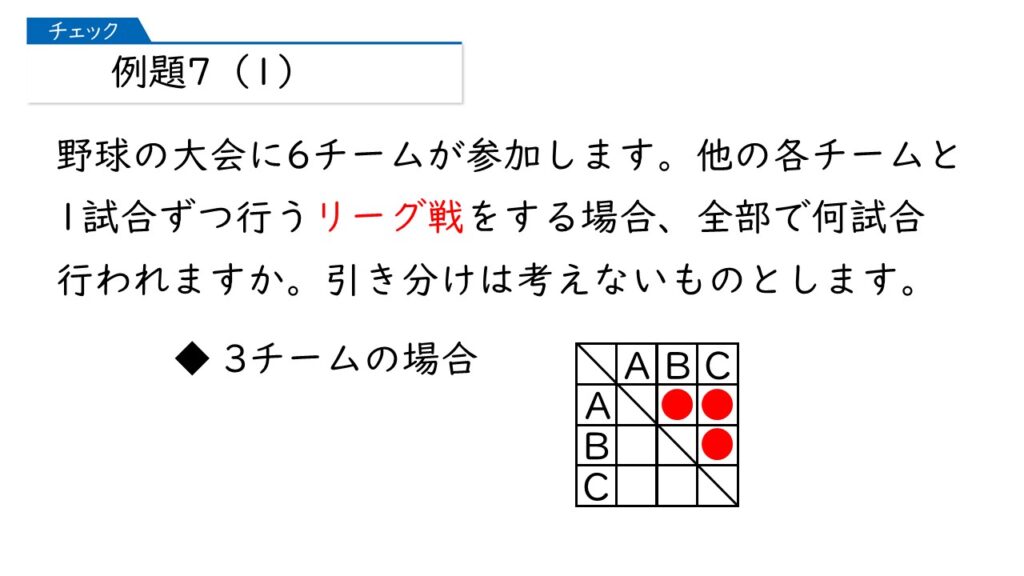
でも、解き方を忘れたときのために、解き方を一緒に導いてみましょう。まず、3チームでリーグ戦を行った場合の試合数は何試合になりますか。
図を書けばカンタンだわ。上の図の赤〇の数だから、3試合ね。
そうですね、図を書けばカンタンです。
しかも、(A,B)と(B,A)は1試合と数えますから、「そうじ当番型」だとわかりますね。
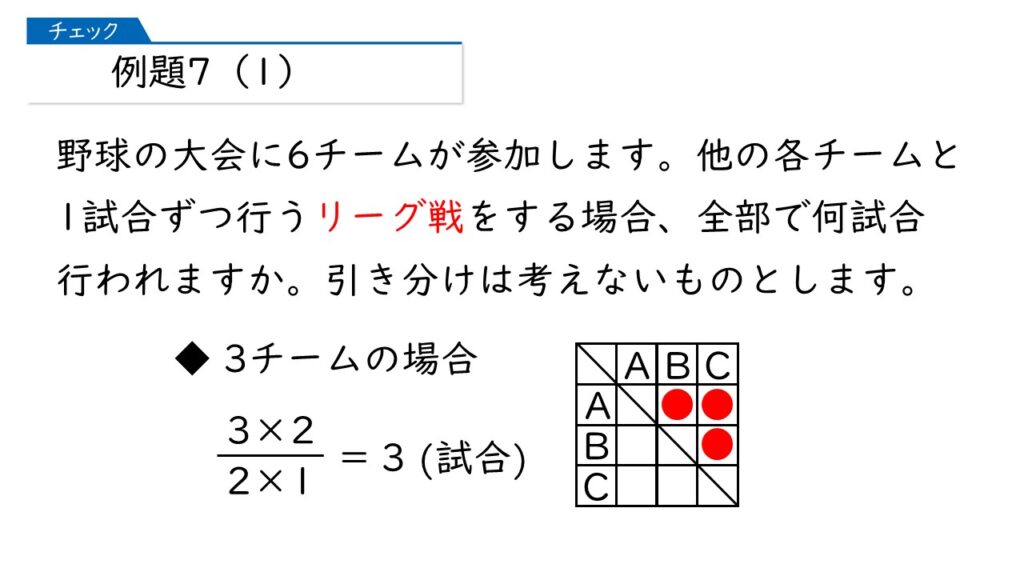
なるほど。3チームの場合、3チームから2チームを選ぶ選び方ということね。
その通りです！ 念のため、4チームの場合も調べましょう。
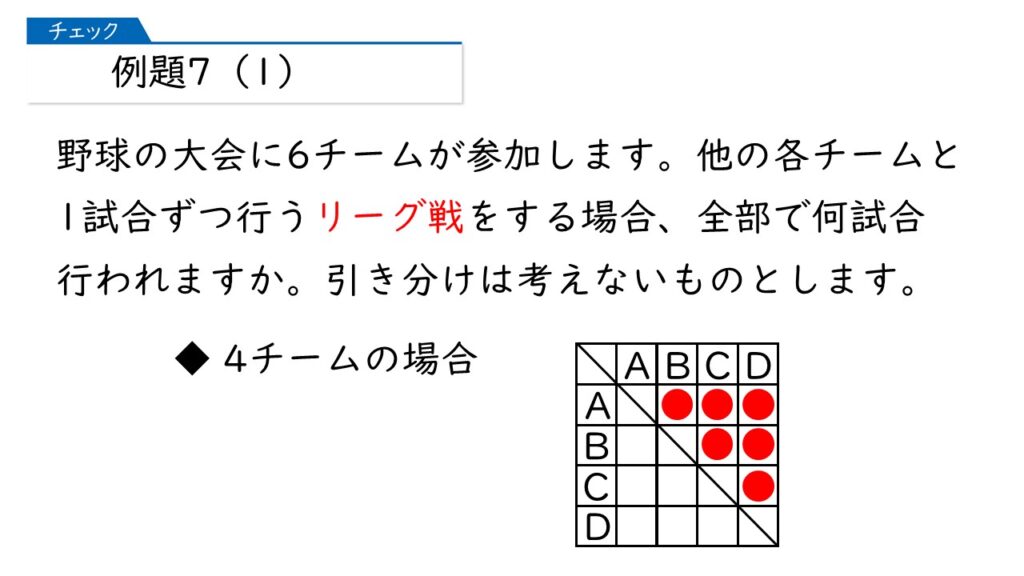
4チームの場合は、4チームから3チームを選ぶ選び方ということね。
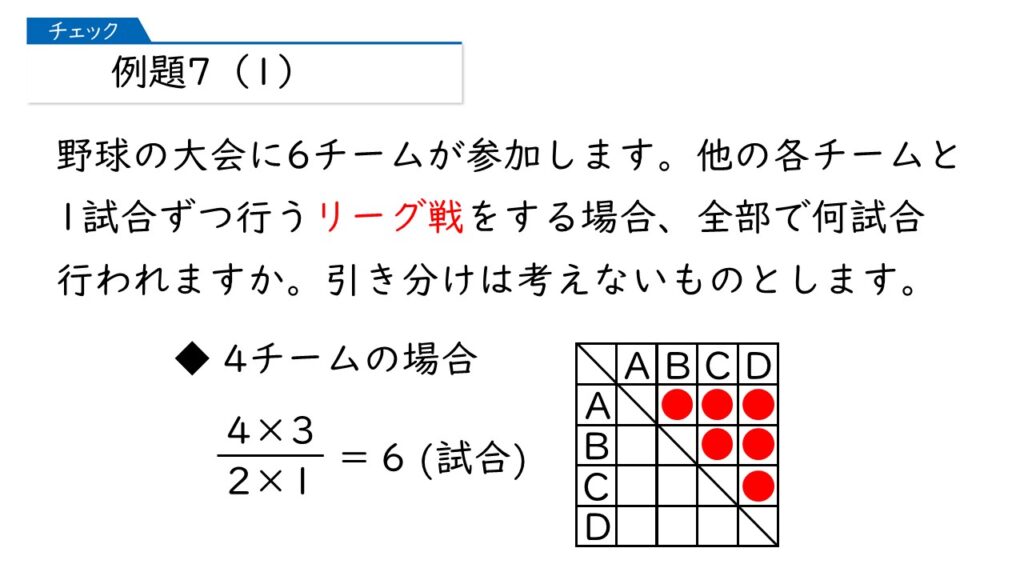
その通りです！ そうすると、6チームの場合の試合数は、次のように求めることができます。
$\dfrac{6×5}{2×1}$＝15（試合）
大事なことは、「公式を覚えること」じゃなくて、「公式の導き方を理解する」ことです！
これは、中学生になっても高校生になっても同じですよ！
例題7（2）の解き方
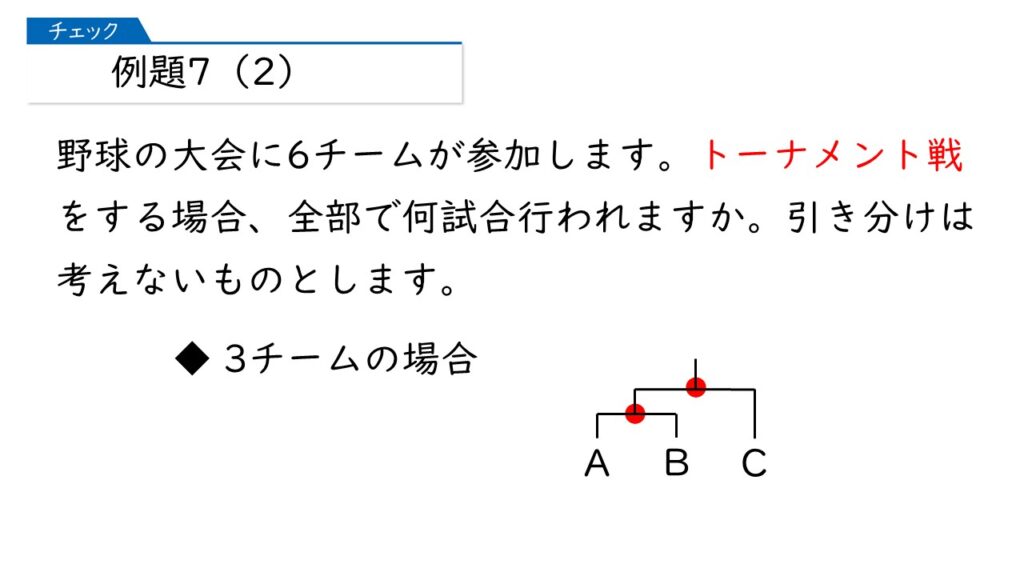
トーナメント戦の場合でも、図を書いて、求め方を考えましょう。まず、3チームの場合の試合数は何試合ですか？
図を書けばカンタンね、2試合だわ。
そうです！ じゃぁ、なぜ2試合になると思いますか。
えっ、なぜかって言われても…
理由聞かれても困りますよね、すみません。
これは、3人いて、そのうちの2人ずつがケンカして、だれか1人が勝つという場面を想定してください。
3人のうち1人だけが勝つということは、負ける人が2人決まる、つまり、負ける人数だけ試合がある、ということなんです。
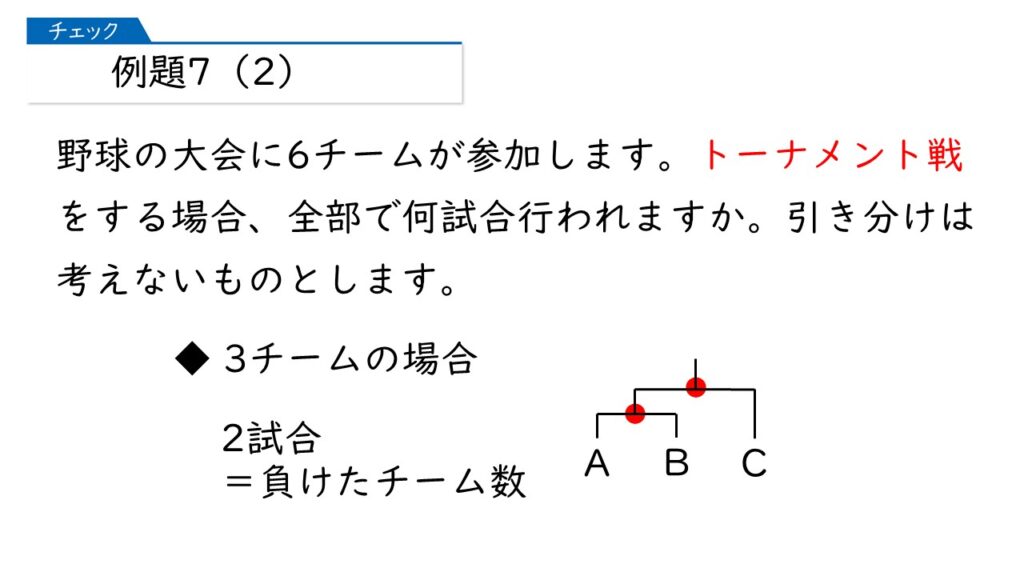
なるほど、分かったわ。そうすると、4チームの場合は、3チームが負けるから、試合数は3試合ね！
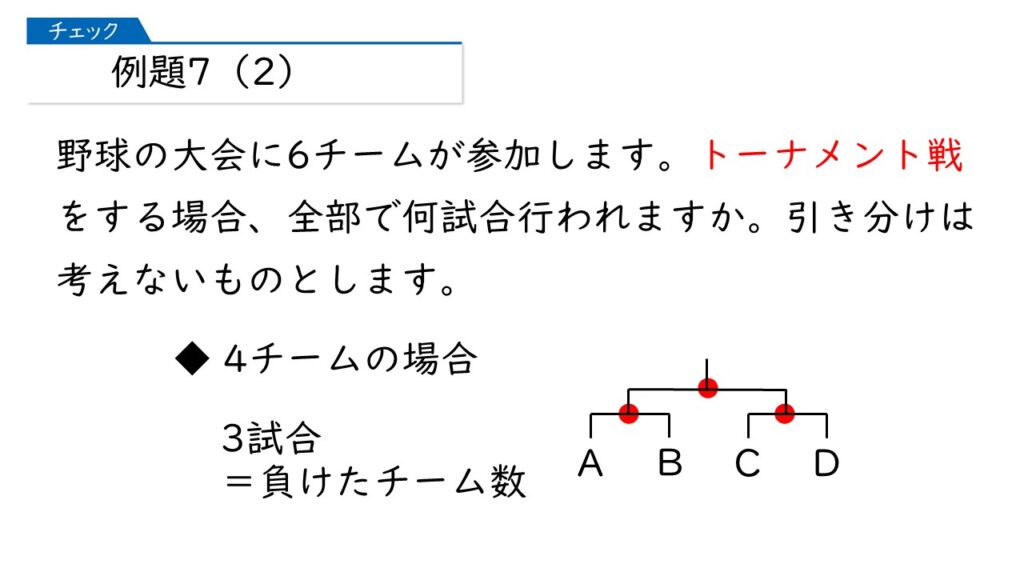
ご名答です！ 結論を言うと、「チーム数－1」が正解になります。
そうすると、6チームあるときは、6－1＝5（試合）が正解ね！
その通りです！
前回と今回で「場合の数」をやりましたが、ここはとても重要な分野ですので、しっかり復習するようにしてくださいね。
わかったわ！
迷ったらまた質問してください！
スポンサーリンク
ABOUT ME
YouTube「クイックラーニング」、学習塾「アカデミーワン」をやっています。中学受験で疑問や不安を抱えている方に、中学受験の本質にさかのぼって、ゆるぎない受験対策ができるようにお手伝いしています。
【著書】「中学受験は親で決まる」（2008年）「優秀な子どもが中学受験で失敗する9の理由」（2010年）
【AERA Kids取材】「9歳10歳の危機」（1012年夏号）、「学力の差は夏で決まる」（2013年秋号）
【著書】「中学受験は親で決まる」（2008年）「優秀な子どもが中学受験で失敗する9の理由」（2010年）
【AERA Kids取材】「9歳10歳の危機」（1012年夏号）、「学力の差は夏で決まる」（2013年秋号）
