四谷大塚 予習シリーズ 算数 徹底解説 5年上第6回 食塩水の濃さ－アカデミーワン
yamada
中学受験マスターガイド
四谷大塚 予習シリーズ 算数 徹底解説 5年上第7回 売買損益－アカデミーワン
yamada
記事内に商品プロモーションを含む場合があります
今回は「売買損益」ですね。
よくお店で「30％引き」とか「5割引き」とかやっているやつね！
そうです！
売買損益の難しいところは「言葉」です。何を求めるのかを把握するのが難しいんです。「原価」とか「仕入れ値」とか「売り値」とか「定価」とか「見込みの利益」とか「実際の利益」とか…。
計算はカンタンなのに、「言葉」でつまづくケースが多いので、お店の人になったつもりになって考えるといいですよ。
この記事の目次
予習シリーズ算数 売買損益 プロローグ
売買損益を取り組むとき、一番最初にやらなければならないことは、次の計算です。
- 「○％引き」「○％増し」
- 「○割○分引き」「○割○分増し」
- 「○の利益を見込んで」
これらを反射的に答えられるようになるために、下の動画を見て練習してくださいね。
予習シリーズ算数 売買損益 例題1
では、例題1(1)からみていきましょう！
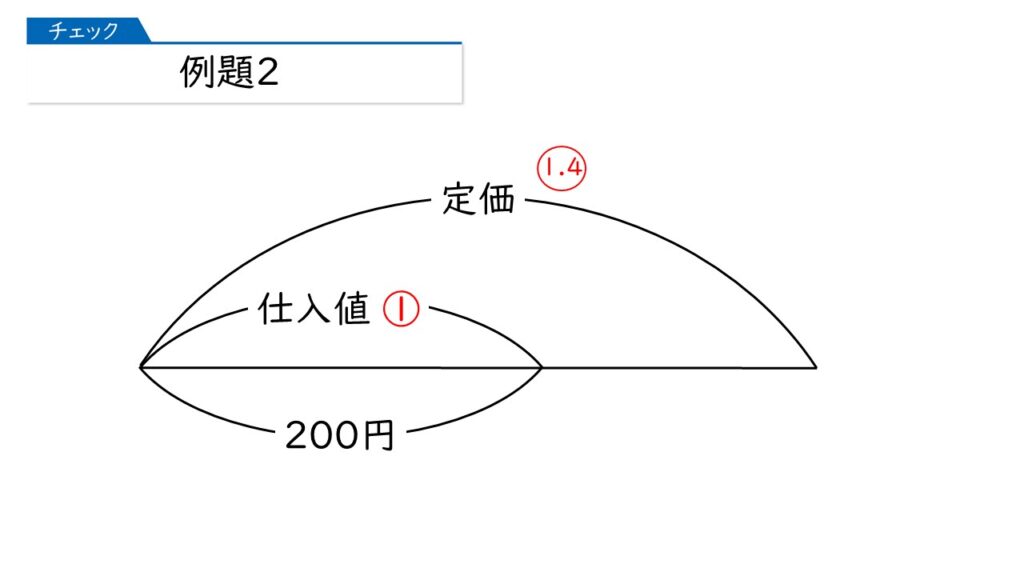
ある品物を200円で仕入れ、仕入れ値の3割の利益を見込んで、□円の定価をつけました。□にあてはまる数を求めなさい。
ポイントは、「仕入れ値の3割の利益を見込んで」のところを、「仕入れ値×1.3（＝定価）」というように、かけ算にすることですね。
なるほど。「～の」のところが「かけ算」になるのね。
そうすると、定価は 200×1.3＝260(円)ね！
その通りです！
では次に、(2)です。
定価800円の品物を、定価の1割5分引きで売ると、売り値は□円になります。□にあてはまる数を求めなさい。
ポイントは、「定価の1割5分引きで売ると」のところを、「定価×(1－0.15)」というように、かけ算にすることですね。
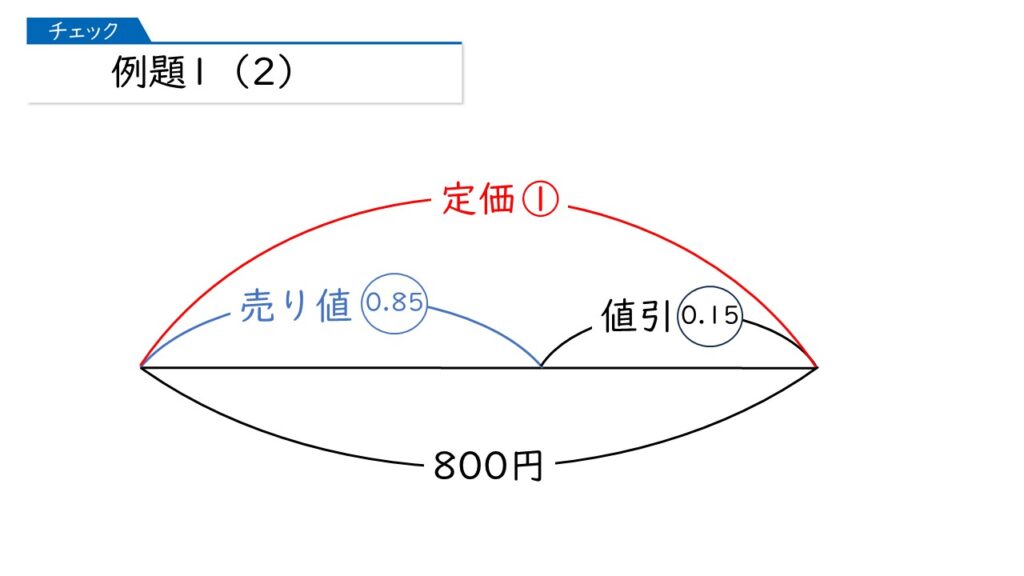
式を立てると、800円×0.85 が売り値になるから、680円が正解ね。
正解です！
では次に、(3)です。
原価□円の品物に、原価の2割増しの480円の定価をつけました。□にあてはまる数を求めなさい。
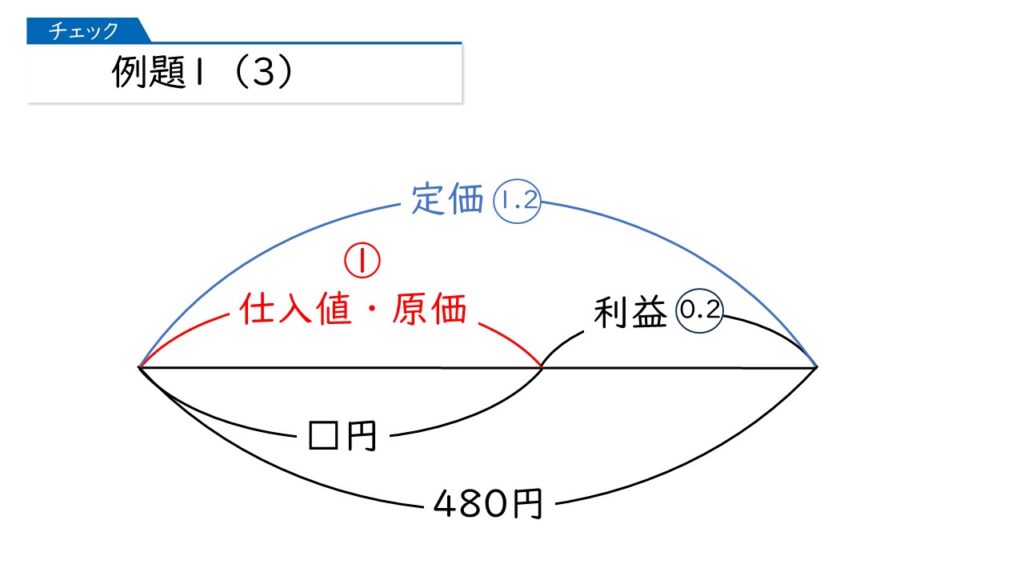
「原価の2割増し」は「原価×(1＋0.2)」ね。
そうすると、□×1.2＝480 だから、答えは、480÷1.2＝400円だわ。
慣れてきましたね！ では次に、(4)です。
定価600円の品物を、定価の□％引きで売ると、売り値は390円になります。□にあてはまる数を求めなさい。
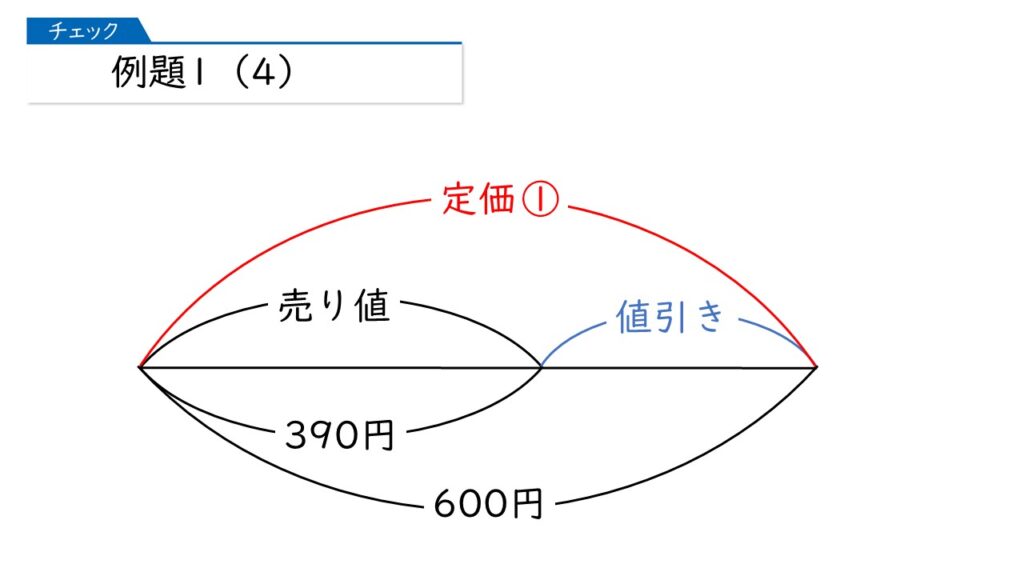
「定価の□％引き」ってあるから、「定価×(1－□)」ってことね。
すると、600×(1－□)＝390円という式がたつわ。
式、合ってますよ、すごいですね！
もちろん、その式を解いて、1－390÷600＝0.35 としてもいいですけど、もっとカンタンに解きましょう。
あっ、そうか！ 値引きした値段が 600－390＝210円だから、210÷600×100＝35％ が答えになるのね。
その通りです！
予習シリーズ算数 売買損益 例題2
さあ、ここからが本番です。 がんばりましょう！
まずは、下の問題文の赤字のところを線分図で表しましょう。
【問題】
ある品物を200円で仕入れ、仕入れ値の4割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の1割引きにしたところ、品物は売れました。利益は何円になりましたか。
大事なことは、問題を読みながら、計算できるところはすぐに計算することです。決して後回しにしてはいけません！
そうか、定価を計算して出せるから、それを真っ先に書く、ということね。定価は、200×1.4＝280円だわ。
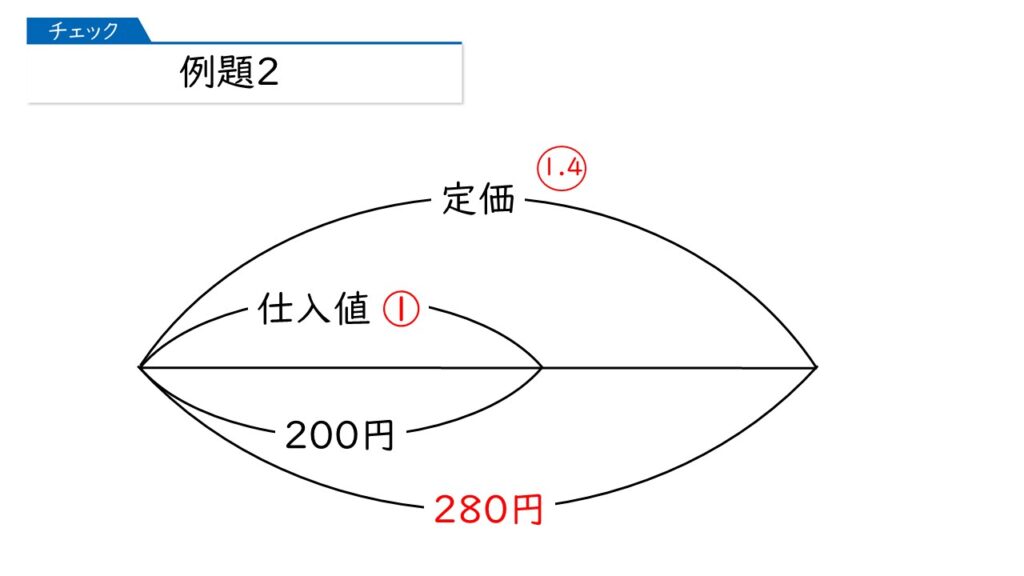
そうですね！
次に、下の問題文の赤字のところを線分図に書き加えましょう。
【問題】
ある品物を200円で仕入れ、仕入れ値の4割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の1割引きにしたところ、品物は売れました。利益は何円になりましたか。
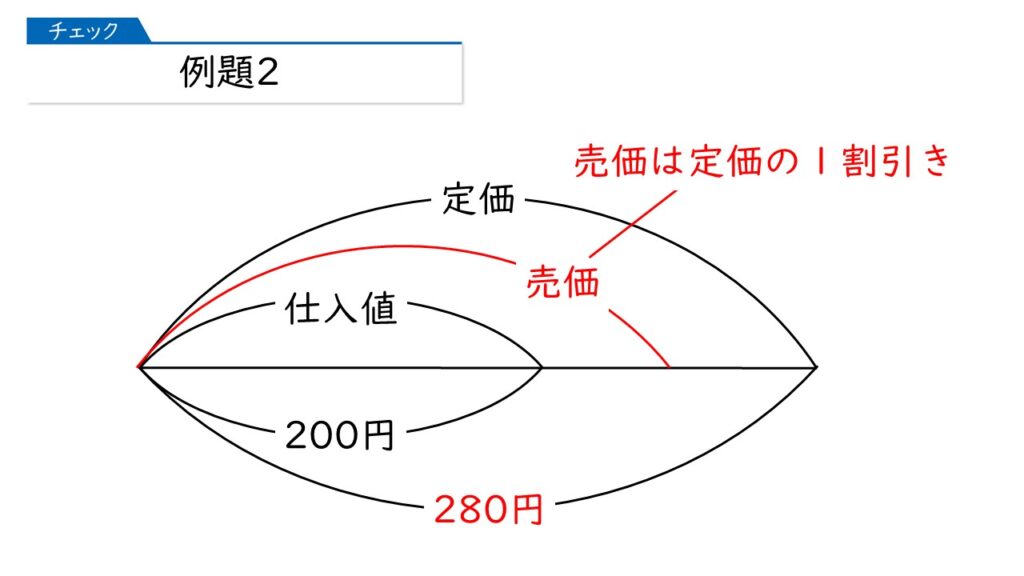
すでに定価が280円と分かってたから、売価は、280円×(1－0.1)＝252円ね！
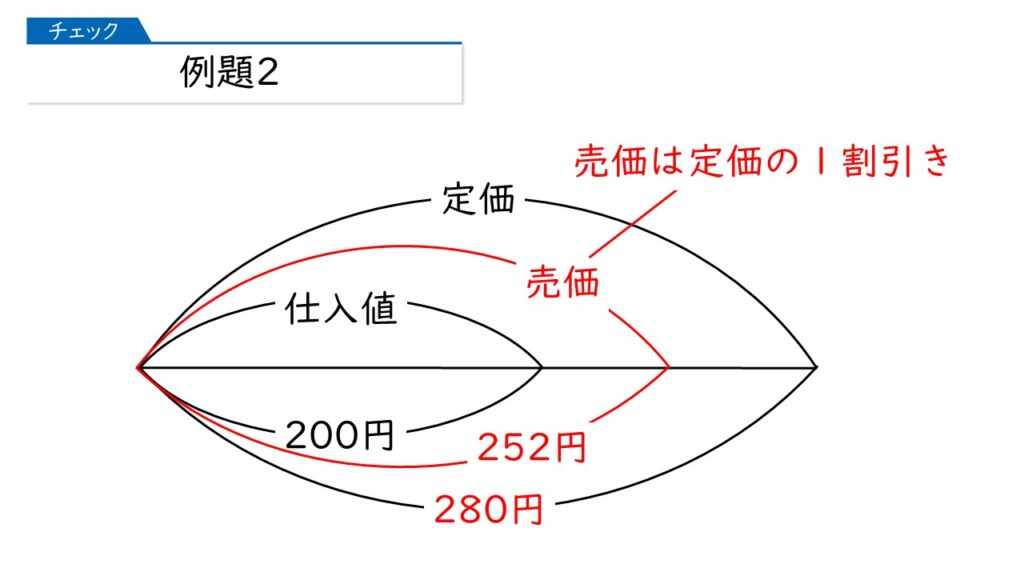
おおお！ スラスラ進んでますね、その通りです！
では、このときの利益は、線分図のどこになりますか？
利益は、売価(収入)から、仕入れ値(支出)を引いたものだから、下の図の太い赤線の部分だと思うわ。
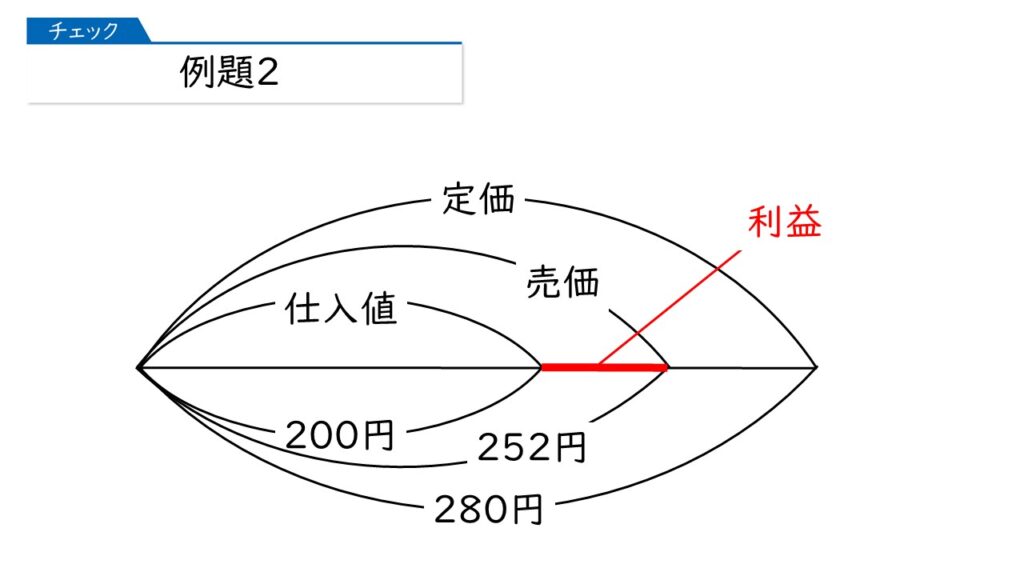
そうですね、その通りです。すると、利益を求めることができますね。
252－200＝52円ね。計算できるところを見逃さないで、どんどん計算を進めていけば、案外、カンタンだと思うわ。
予習シリーズ算数 売買損益 例題3
さあ、どんどん行きましょう！ 例題3はとても重要な問題です。
まずは、下の問題文の赤字のところを線分図で表しましょう。
【問題】
ある品物に、仕入れ値の4割の利益を見込んで定価をつけました。しかし、定価では売れ残ったので、定価の2割引きにしたところ、品物は売れて利益は150円になりました。この品物の仕入れ値は何円ですか。
あら。仕入れ値が分かっていないから、定価を出すことはできないわ…
そう、それでいいんです。さらに、下の問題文の赤字のところを、線分図に書き加えていきましょう。
【問題】
ある品物に、仕入れ値の4割の利益を見込んで定価をつけました。しかし、定価では売れ残ったので、定価の2割引きにしたところ、品物は売れて利益は150円になりました。この品物の仕入れ値は何円ですか。
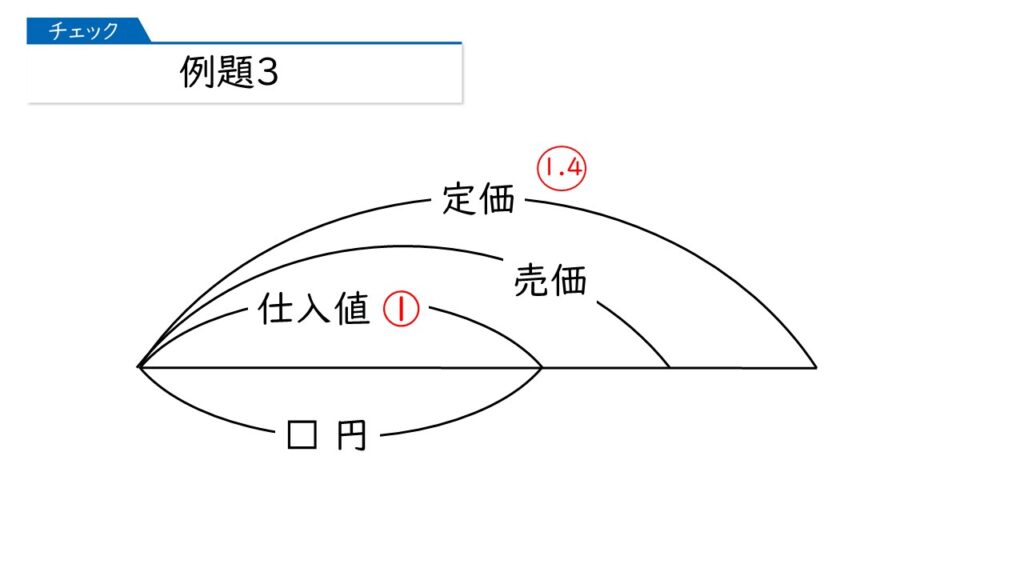
仕入れ値の割合を①としたとき、定価の割合が $\mymaru{1}{4}$ 、ですね。
さらに、「定価では売れ残ったので、定価の2割引きにした」とあることから、仕入れ値の割合を①としたときの売価の割合はいくつになりますか？
定価の割合 $\mymaru{1}{4}$ の(1－0.2)倍、ってことね！
その通りです、すごいですね！ 仕入れ値をもとにして、定価や売価の割合を求めるパターンなんです。
では最後に、下の問題文の赤字のところを、線分図に書き込みましょう。
【問題】
ある品物に、仕入れ値の4割の利益を見込んで定価をつけました。しかし、定価では売れ残ったので、定価の2割引きにしたところ、品物は売れて利益は150円になりました。この品物の仕入れ値は何円ですか。
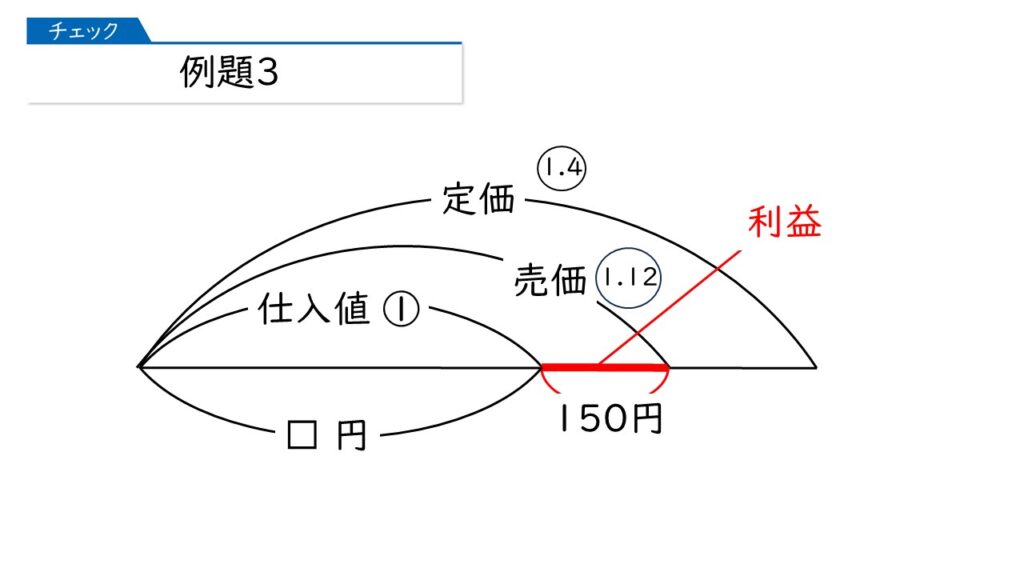
ここからがちょっと難しいです。
仕入れ値の割合を①としたときの利益の割合が分かれば、仕入れ値×(利益の割合)＝150円になります。
利益の割合は、売価の割合から仕入れ値の割合を引けば出るわ。
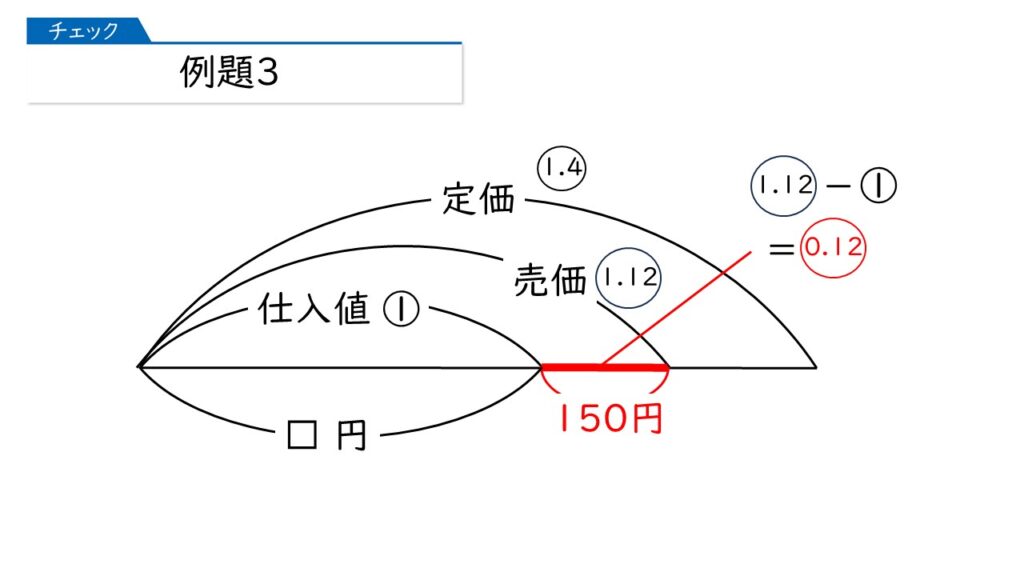
そすると、仕入れ値×0.12＝150円だから、仕入れ値は、150÷0.12＝1250円なのね。
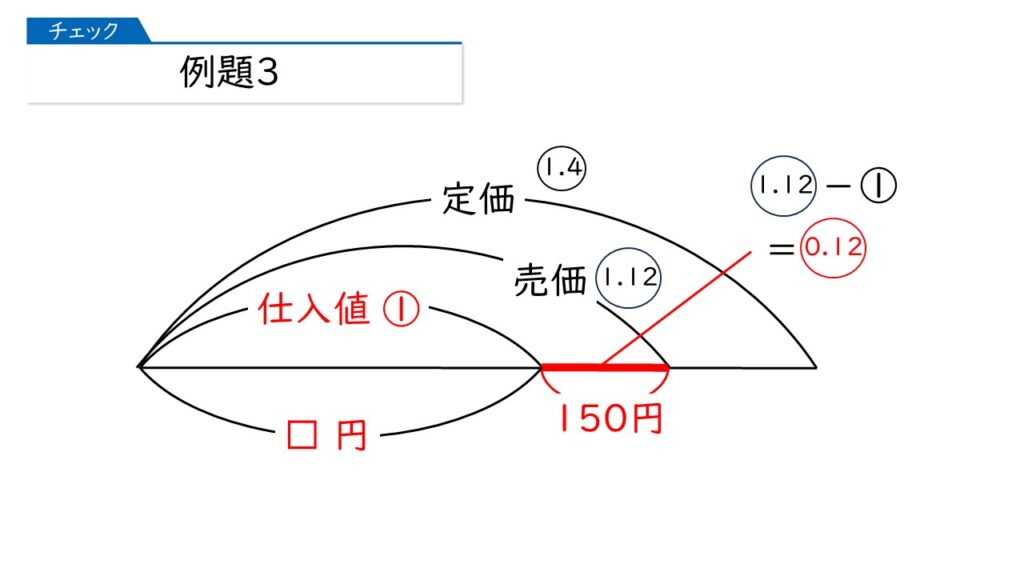
大正解です、おめでとうございます！
仕入れ値を①とおいて、この割合をもとに、ほかの値の割合を表す、とうのがポイントですね。
そうすると、上の図で「仕入れ値×0.12＝150円」という関係を導くことができるんです。
慣れが必要ですので、すぐに類題を解いてくださいね！
予習シリーズ算数 売買損益 例題4
続いて、例題4です。
まずは、下の問題文の赤字のところを線分図で表しましょう。
【問題】
ある品物を、定価の1割引きで売ると105円の利益になり、定価の3割引きで売ると45円の損失になります。
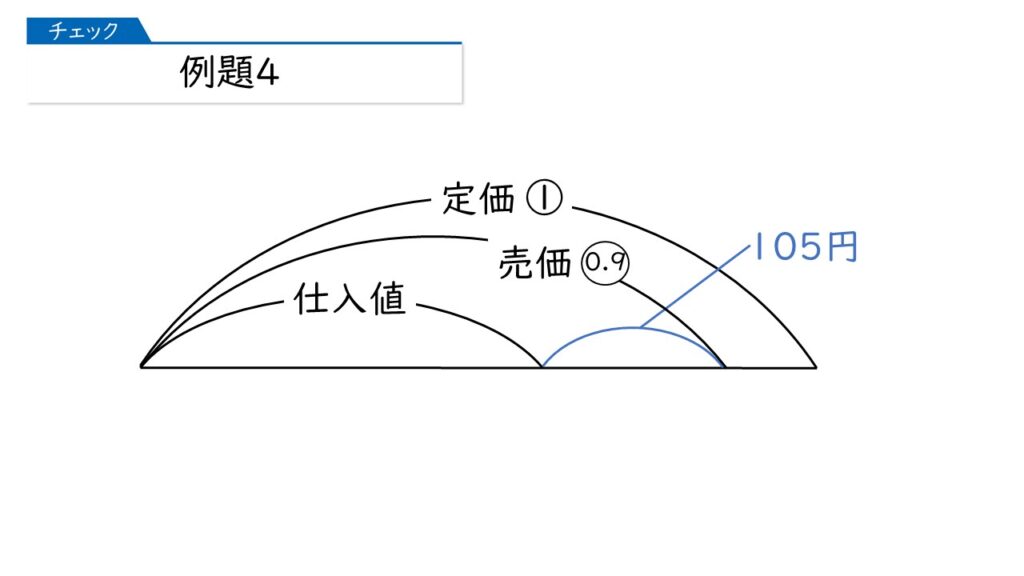
次に、下の問題文の赤字のところを線分図に書き加えましょう。
【問題】
ある品物を、定価の1割引きで売ると105円の利益になり、定価の3割引きで売ると45円の損失になります。
そうすると、(1)は解けますか？
【問題】
ある品物を、定価の1割引きで売ると105円の利益になり、定価の3割引きで売ると45円の損失になります。
(1) この品物の定価は何円ですか。
(2) この品物の仕入れ値は何円ですか。
定価を①としたとき、$\mymaru{0}{9}$－$\mymaru{0}{7}$ ＝ $\mymaru{0}{2}$ にあたるのが、105＋45＝150円ということですね！
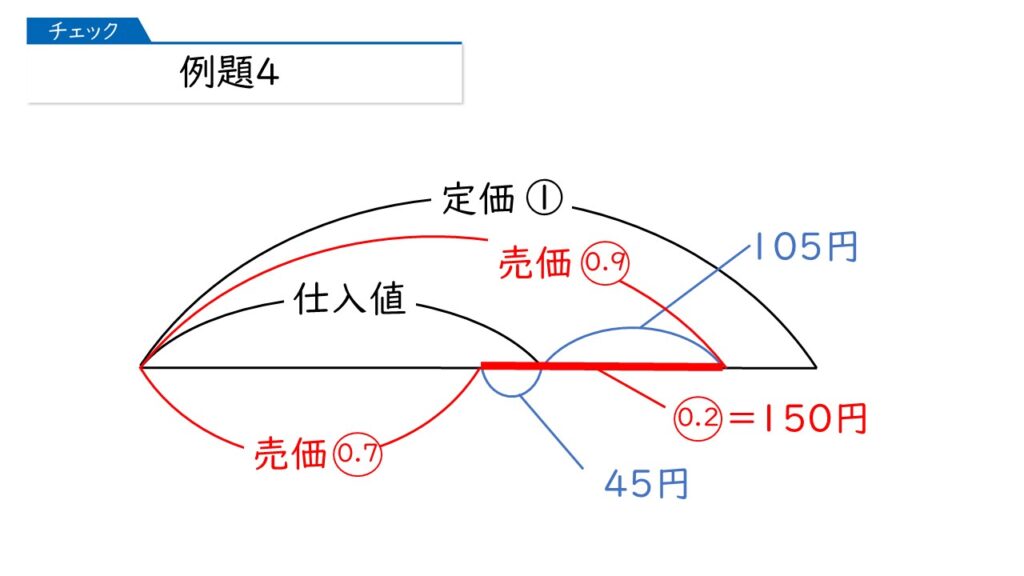
そうです！ 「定価×0.2＝150円」なので、定価は、150÷0.2＝750円になりますね。
そうすると、(2)の仕入れ値も求めることができるわ。
「定価の1割引きで売ると105円の利益になる」から、750×0.9－105＝570円ね。
さすがです！
これまでやってきたように、売買損益の問題では、「原価と定価と売価を線分図で表す練習」がとても大事です。
類題などでも、同じように解いてみてくださいね。
予習シリーズ算数 売買損益 例題5
次は例題5ですね。まずは問題を読んでみましょう。
まず、仕入れで、200円×100個＝20,000円使っていますね。つまり、初めに20,000円支出しているんですね。
問題では「全体の利益は何円になりましたか」と聞いていますから、売り上げた金額、つまり収入額が分かればいいですね。
では、問題を読み進めながら、整理していきましょう。下の問題文の赤字のところ（1日目）では、どれだけの売り上げ（収入）があったか分かりますか。
1個あたりの定価が 200×1.5＝300円で、100－30＝70個売れたわけね。そうすると、売り上げ（収入）は、300×70＝21,000円だわ。
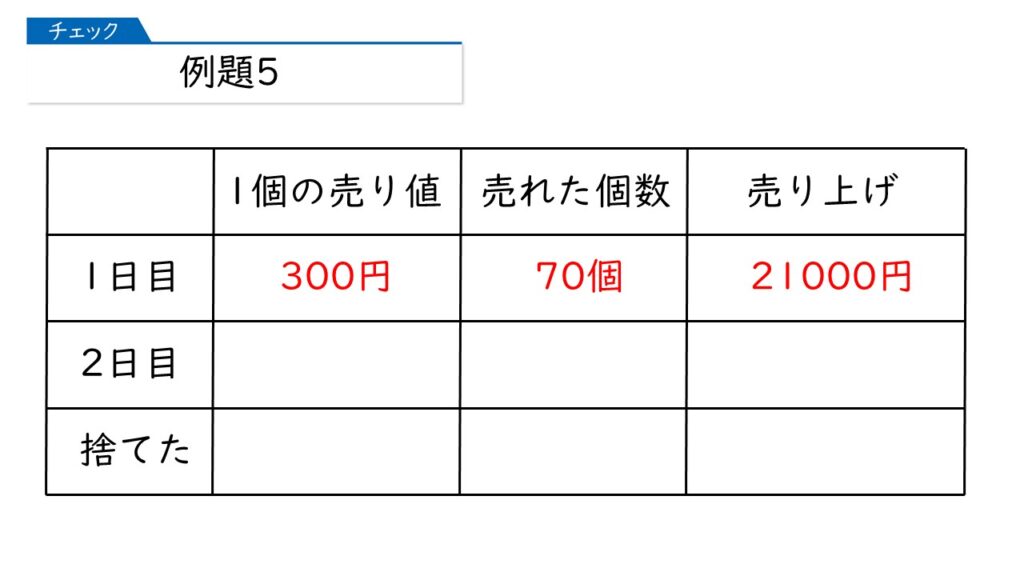
その通りです！
では、下の問題文の赤字のところ（2日目）では、どれだけの売り上げ（収入）がありましたか？
1個あたりの定価が 300×0.8＝240円で、30－10＝20個売れたわけね。そうすると、売り上げ（収入）は、240×20＝4,800円だわ。
その通りです、問題をよく読めていますね！
では最後に、下の問題文の赤字のところは、どのように考えたらいいですか？
捨てちゃったわけだから、ここからは売り上げ（収入）はゼロってことかしら？
はい、そうなります！
そうすると、売り上げ（収入）は、21,000円＋4,800円＝25,800円ね。
答えがでたわ。利益は、25,800円－20,000円＝5,800円よ。
大正解です！ おめでとうございます。計算ミスをしないように注意して、類題をやってみましょう。
予習シリーズ算数 売買損益 例題6
例題6の解き方
次は例題6ですね。まずは問題を読んでみましょう。
仕入れたミカンの中に、くさっていなかったものと、くさっていたもの(6個)が混じっていますね。
あと、全体の利益が810円とありますが、これはつまり、売り上げ（収入）と仕入れ（支出）の差が810円ということです。
この点に注意して図を書いてみます。
しかし、売れた個数は見当もつかないわ…
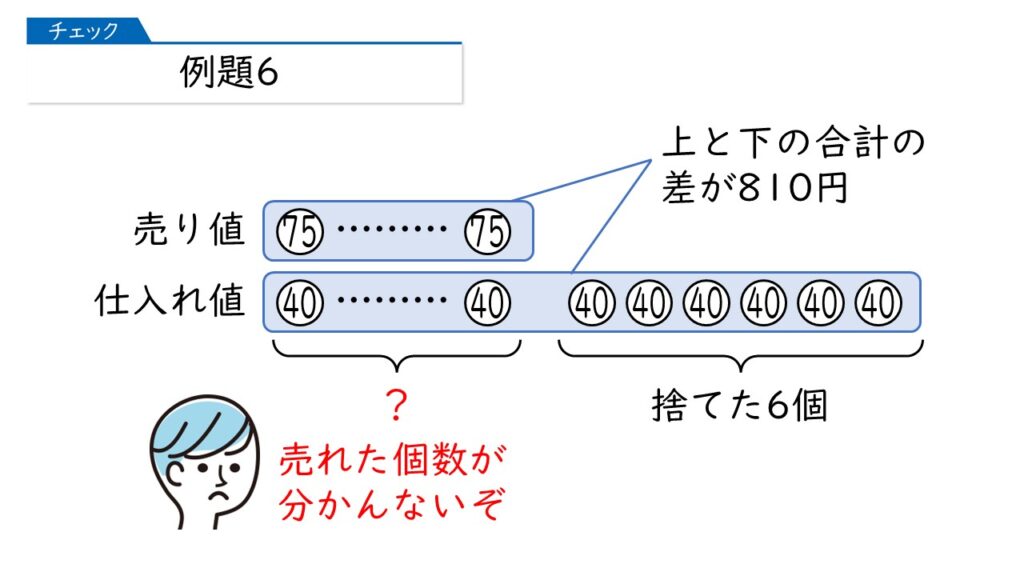
そうですよね。
でも、これって「差集め算」なんですよ。差集め算のポイントは何だったでしょうか。
確か…、「上段と下段の数をそろえる」たっだかしら。
そうです、その通りです！
下の図のように、仮に「捨てた6個がもし売れてたら…」と考えるんですね。
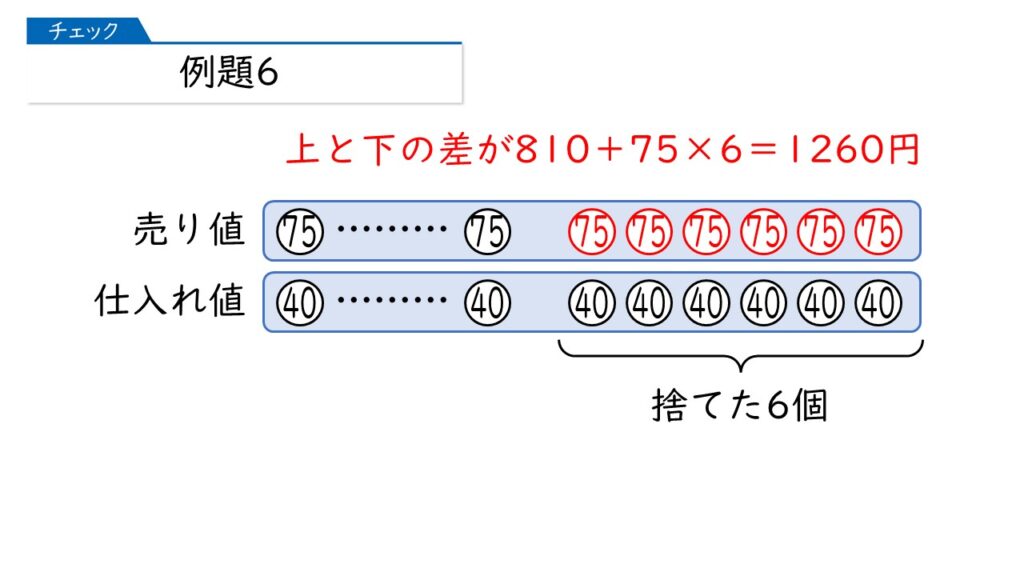
そうすると、売り上げ（収入＝上段）と、仕入れ（支出＝下段）の差が広がって、1260円になるんですね。
こうすれば、1個当たりの利益が35円ですから、仕入れたミカンの個数を求めることができます。
なるほど。仕入れたミカンの個数は、1260÷35＝36個になるわけね。
例題6をマルイチ算で解く
「いろいろな差集め算(5年上 第4回)」のときにお話ししましたが、差集め算のほとんどの問題はマルイチ算で解決することができます。
ですので、ここでもマルイチ算で解いてみいたいと思います。
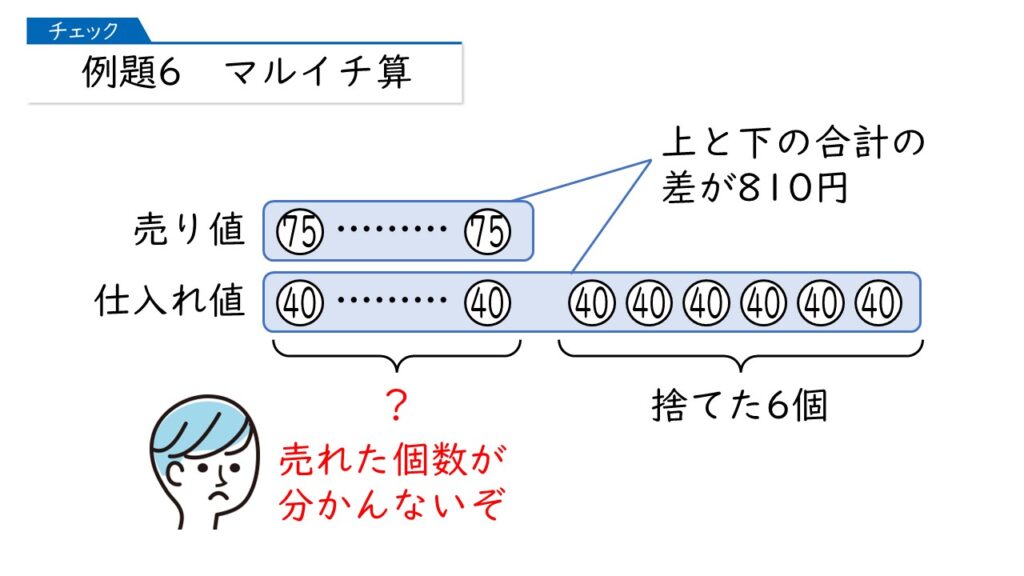
この問題では、売れた個数が分かれば、それに6を足せばいいだけです。ですので、売れた個数を①とおきます。
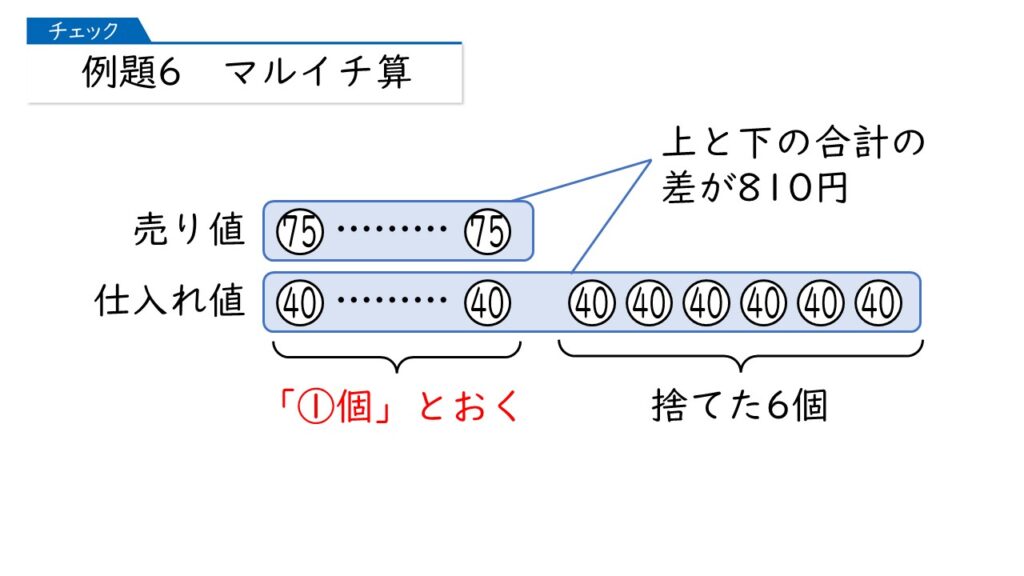
そうすると、売り上げ（収入＝上段）と、仕入れ（支出＝下段）の差が810円であることに注意して、次のような式を立てて解くことができます。
75円×①個＝40円×(①個＋6個)＋810
$\maruii{75}$＝$\maruii{40}$＋240＋810
$\maruii{35}$＝1050
①＝30個
以上から、仕入れた個数は30＋6＝36個になります。
予習シリーズ算数 売買損益 例題7
例題7の解き方
いよいよ最後、例題7です。あと少しですので、がんばりましょう！ まずは問題文です。
【例題7】は【例題6】に似てますね。まず、1日目を下の図のように整理しましょう。
同じようにして、2日目も書き込みましょう。
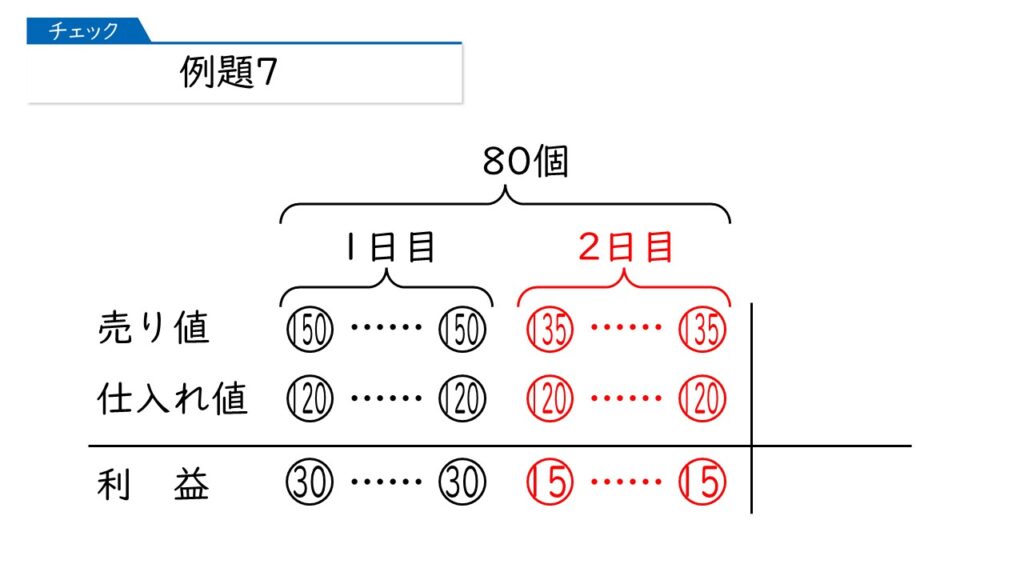
そして、2日目までで全部が売れて利益がでました。これも図に書き加えましょう。
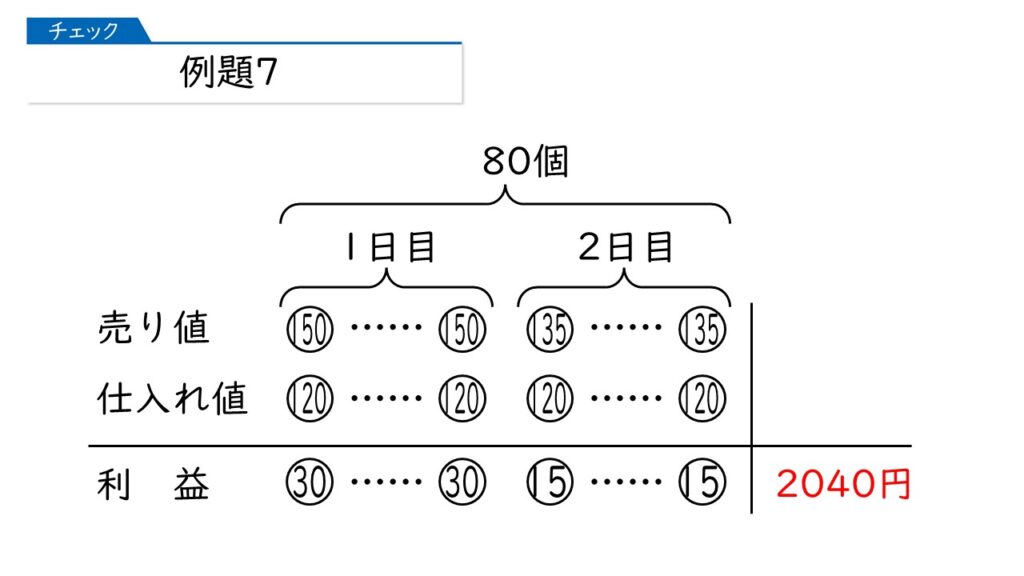
そうすると、この問題では、「売れた合計の個数」と「利益の合計」が分かっていますね。
これはもうやったことがありますが、何算でしょうか？
つるかめ算ね！ 「つるが○羽、かめが○匹いて、つるとかめを合わせていくつ、足の合計がいくつ」って感じの。
まさに、そうです！
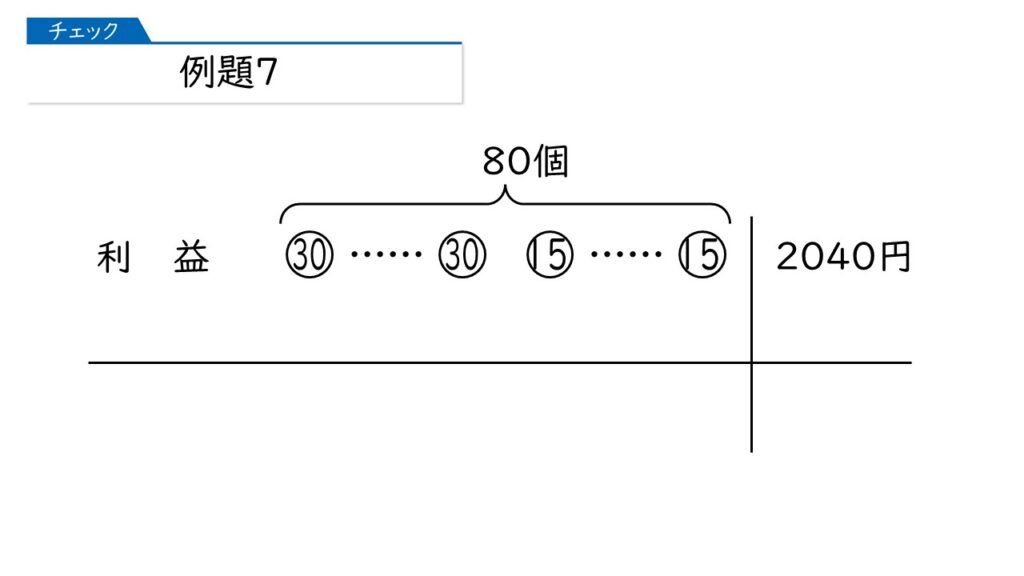
問題では「2日目に売れた個数」を聞いていますから、反対の、つまりすべて1日目の利益が出た、と考えます。その場合、利益の合計は、30×80＝2400円ですね。
そうすると、上段と下段の差に注目すればいいのね。
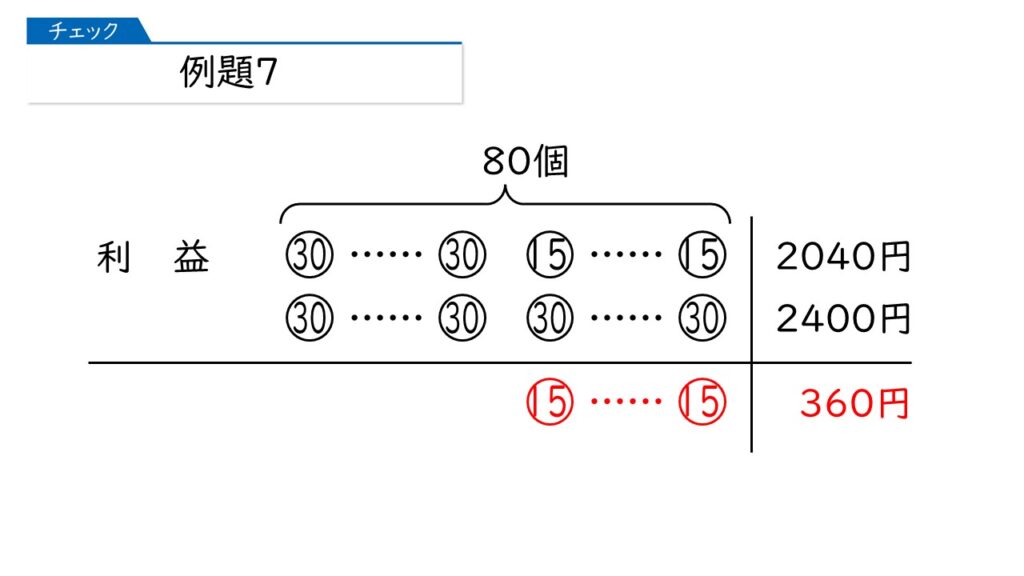
そうです！
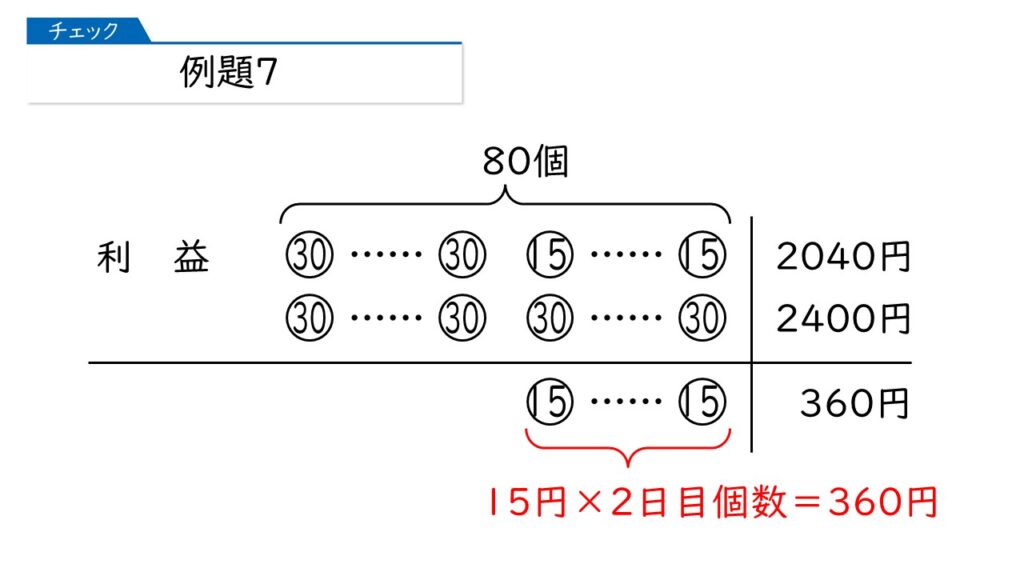
そうすると、2日目に売れた個数は、360÷15＝24個になるわ。
大正解です！ ここでは図を書きましたが、できればですけれど、つるかめ算は図を書かないで解けるようにしましょう。
例題7をマルイチ算で解く
つるかめ算は差集め算の一種ですので、マルイチ算で解くことができます。
やってみますね。2日目に売れた個数を求めますので、2日目に売れた個数を①個とおきます。
そうすると、1日目に売れた個数が(80－①)個になります。
利益のところに注目して、次の計算式で解くことができます。
30円×(80－①)個＋15円×①個＝2040円
2400－㉚＋⑮＝2040
2400－⑮＝2040
⑮＝360
①＝24個
マルイチ算では、式を立てるのが難しいわ。
確かにそうですね。
ただ、マルイチ算は慣れれば強い武器になりますし、上位生のほとんどはマルイチ算でいくので、マルイチ算の解き方を見守ってくれる人がいればこちらでいったほうがいいかもしれません。
差集め算のときの練習問題をここでもダウンロードできるようにしましたので、マルイチ算でいくと腹を決めた人は練習してください。
マルイチ算の応用問題 (103 ダウンロード )分かったわ。試してみますね。今日もありがとうございました！
こちらこそ、いつもありがとうございます。ご質問があれば、下のフォームからお問い合わせください！
中学受験についてのほかの記事もぜひ参考にしてくださいね。
|
|
スポンサーリンク
ABOUT ME
YouTube「クイックラーニング」、学習塾「アカデミーワン」をやっています。中学受験で疑問や不安を抱えている方に、中学受験の本質にさかのぼって、ゆるぎない受験対策ができるようにお手伝いしています。
【著書】「中学受験は親で決まる」（2008年）「優秀な子どもが中学受験で失敗する9の理由」（2010年）
【AERA Kids取材】「9歳10歳の危機」（1012年夏号）、「学力の差は夏で決まる」（2013年秋号）
【著書】「中学受験は親で決まる」（2008年）「優秀な子どもが中学受験で失敗する9の理由」（2010年）
【AERA Kids取材】「9歳10歳の危機」（1012年夏号）、「学力の差は夏で決まる」（2013年秋号）
